A conducting disc of radius r rotates with a small but constant angular velocity co about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
V at a distance r/2From the centre = rω/2
Related Solutions
A conducting disc of radius r rotaes with a small but constant angular velocity about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA non-conducting disc having unifrom positive charge Q , is rotating about its axis with unifrom angular velocity omega .The magnetic field at the centre of the disc is.
View SolutionA non-conducting disc having unifrom positive charge , is rotating about its axis with unifrom angular velocity .The magnetic field at the centre of the disc is.

View SolutionIn a Faraday disc dynamo, a metal disc of radius R rotates with an angular velocity @about an axis perpendicular to the plane of the disc and passing through its centre. The disc is placed in a magnetic field B acting perpendicular to the plane of the disc. Determine the induced emf between the rim and the axis of the disc.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionA charge is uniformly distributed on a non-conducting disc of radius . It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R . It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA rod of length l rotates with a small but uniform angular velocity about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA rod of length l rotates with a small but uniform angular velocity about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA rod of length l rotates with a small but uniform angular velocity about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity omega in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
View SolutionA conducting disc of radius R is placed in a uniform and constant magnetic field B parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are e and m )
View SolutionA conducting disc of radius is placed in a uniform and constant magnetic field parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are and )
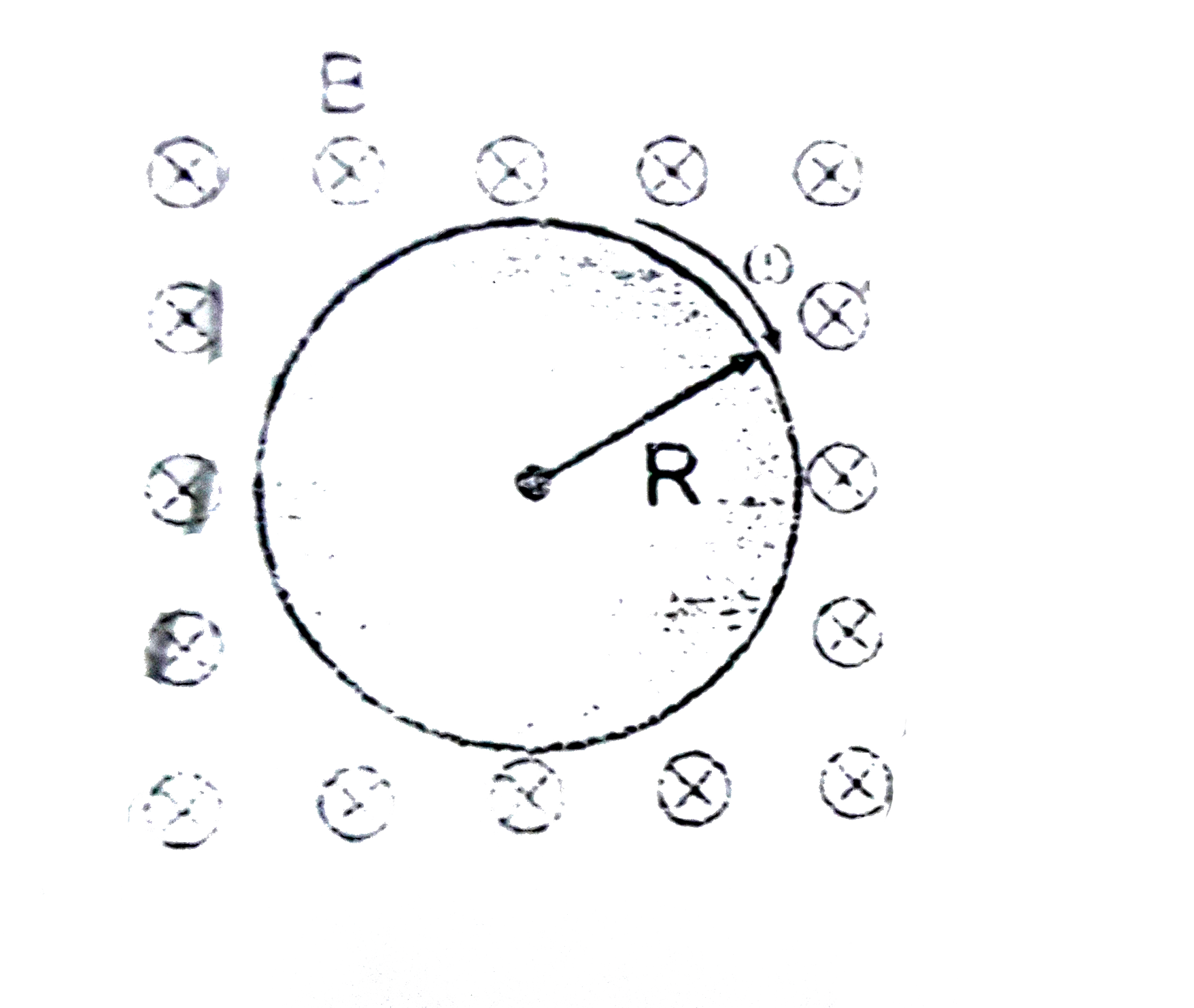
View SolutionA metal disc of radius R = 25 cm rotates with a constant angular velocity omega = 130 rad s^(-1) about its axis. Find the potential difference between the center and rim of the disc if (a) the external magnetic field is absent, (b) the external uniform magnetic field B = 5.0 mT directed perpendicular to the disc.
View SolutionIn a Faraday disc dynamo, a metal disc of radius R rotates with an angular velocity about an axis perpendicular to the plane of the disc and passing through its centre.The disc is placed in a magnetic field B acting perpendicular to the plane of the disc.Determine the induced emf between the rim and the axis of the disc.
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
View SolutionA metal disc of radius R = 25 cm rotates with a constant angular velocity omega = 130 rad s^(-1) about its axis. Find the potential difference between the center and rim of the disc if (a) the external magnetic field is absent, (b) the external uniform megnetic field B = 5.0 mT directed perpendicular to the disc.
View Solution