Suppose the rod with the balls A and B of the previous problem is clamped at the centre in such a way that it can rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a height h on the ball B. The particle collides with B and sticks to it. a Find the angular momentum and the angular speed of the system just after the collision. b*What should be the minimum value of h so that the system makes a full rotation after the collision.
The system is kept rest in the horizontal position and a particle P falls from a height h and collides with B and sticks to it.Therefore angular momentum of the rod just after the collision When the mass 2m will at the top most position and the mass m at the lowest point they will automatically rotate. In this position the total gain in potential energy = 2 mg × l/2 – mg l/2 = mgl/2
Related Solutions
Suppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
View SolutionSuppose the rod with the balls A and B of theprevious problem is clamped at the centre in such a way that it ca rotate freely about a horizontal axis through the clamp. The system is kept at rest in the horizontal position. A particle P of the same mass m is dropped from a heigh h hon the ball B. The particle collides with B and sticks to it. a. Find the angular momentum and the angular speed of the system just after the collision. b. What should be the minimum value of h so that the system makes a full rotation after the collision.
View SolutionTwo small balls A and B, each of mass m are joined rigidly by a light horizontal rod of length L. The rod is clamped at the centre in such a way that it can rotate free about a vertical axis through its centre. The system is rotated with an angular speed about the axis. A particle P of mass m kept at rest sticks to the ball A as the ball collides with it. The new angular speed of the rod is then value of y.
View SolutionTwo small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.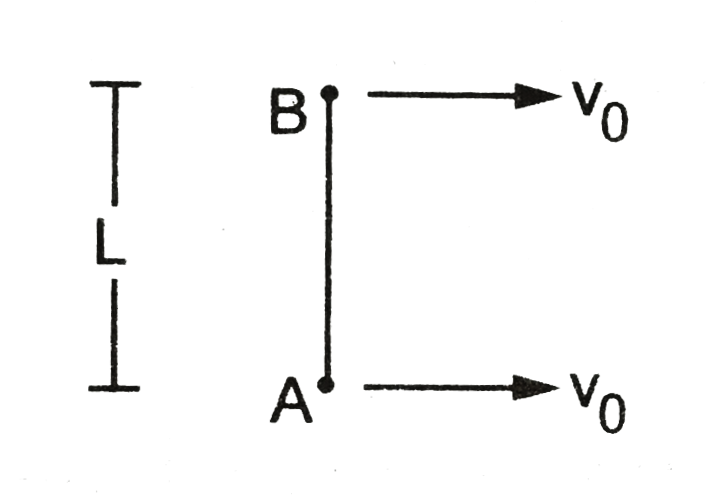
View SolutionTwo small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.
View SolutionL लबाई की एक एकसमान छड़ के दानों किनारों पर 1 द्रव्यमान की गेंद लगी है। यह छड़ अपने मध्यबिंदु से जाते लंबवत अक्ष के परित स्वतंत्र रूप से घूम सकती है। यह अक्ष क्षैतिज अवरथा में रहता है। प्रारंभ में निकाय को क्षैतिज अवस्था में रखा गया है। गैंद B पर h ऊँचाई से समान द्रव्यमान n का एक कण P गिराया जाता है। कण गेंद B से टकराकर चिपक जाता है
(a) टक्कर के तुरंत बाद निकाय का कोणीय संवेग तथा कोणीय चाल ज्ञात करें।
(b) h का न्यूनतम मान कितना होना चाहिए ताकि टक्कर के बाद निकाय एक पूरा चक्कर लगा पाए
View SolutionOne end of a uniform rod of mass m and length / is clamped. The rod lies on a smooth horizontal surface and rotates on it about the clamped end at a uniform angular velocity . The force exerted by the clamp on the rod has a horizontal component.
View SolutionL लबाई की नगण्य भार वाली क्षैतिज छड़ के दोनों सिरों पर m द्रव्यमान बाली दो छोटी गेदे दृढ़तापूर्वक जोड़ी गई है। छड़ अपने केंद्र से गुजरनेवाले ऊर्ध्वाधर अक्ष के परितः स्वतंत्र रूप से घूम सकती है। निकाय को अक्ष के परितः कोणीय चाल से घुमाया जाता है। स्थिर अवस्था में रखा हुआ द्रव्यमान का एक कण P एक गेंद से टकरा जाता है और उसमें चिपक जाता है। छड़ की नई कोणीय चाल ज्ञात करे
View Solutionएक गेंद A को किसी ऊँचाई से गिराया जाता है तथा दूसरी गेंद B को उसी ऊँचाई से 5 मी/से की चाल से क्षैतिज दिशा में फेंका जाता है | सही कथन है -
View SolutionA uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.
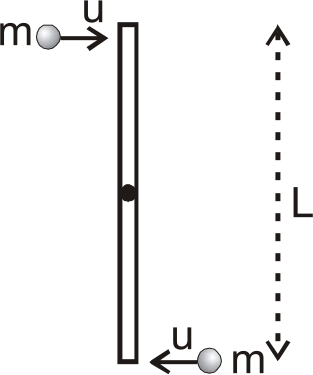
View SolutionA uniform rod of mass 200 grams and length L = 1m is initially at rest in vertical position. The rod is hinged at centre such that it can rotate freely without friction about a fixed horizontal axis passing through its centre. Two particles of mass m = 100 grams each having horizontal velocity of equal magnitude u = 6 m/s strike the rod at top and bottom simultaneously as shown and stick to the rod. Find the angular speed (in rad/sec.) of rod when it becomes horizontal.

View SolutionAn uniform rod of mass and length is free to rotate about a horizontal axis passing through its centre. A particle of mass falls vertically through a height and collides elastically with the rod at a distance from . at the instant of collision the rod was stationary and was at angle with horizontal as shown in figure
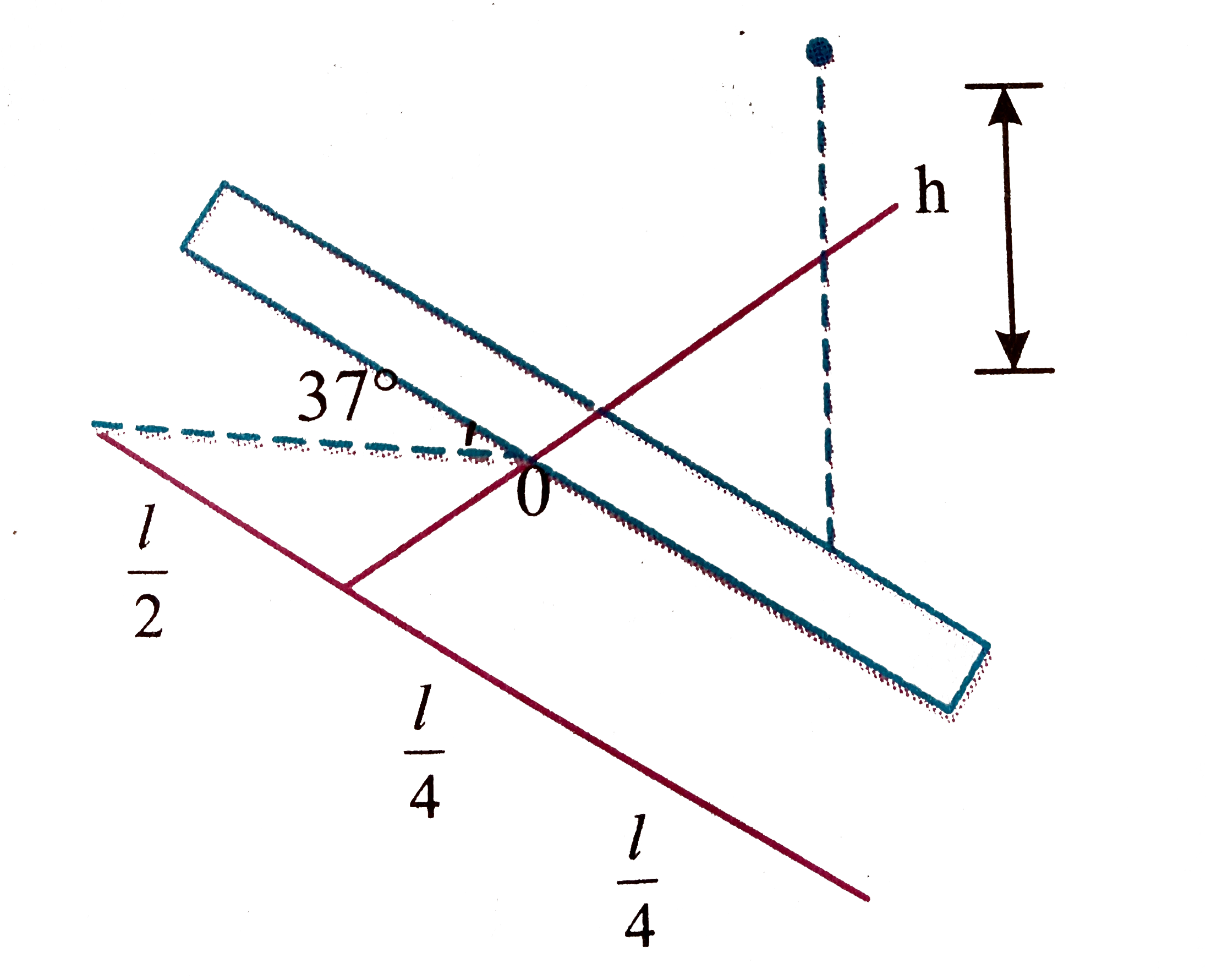
Velocity of particle after collision
View SolutionIn the figure shown, the cart of mass 6m is initially at rest. A particle of mass m is attached to the end of the light rod which can rotate freely about A. If the rod is released from rest in a horizontal position shown, determine the velocity of the particle with respect to the cart when the rod is vertical. (Assume frictionless surface)

View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
View SolutionA particle of mass is projected with a speed at an angle with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
When the particle is at maximum height and
When the particle is just about to collide with the horizontal surface
View SolutionA particle of mass is projected with a speed at an angle with the horizontal. Find the angular momentum of the particle about an axis passing through point of projection and perpendicular to the plane of motion of the particle.
When the particle is at maximum height and
When the particle is just about to collide with the horizontal surface
View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.
View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.

View Solution