Find the velocity of the particle for the time interval t = 0 to t = 5s and t = 10 sec. from the given graph.
Velocity for the time interval t = 0 to t = 5s v = 10-0/5-0 = 2ms-1.Velocity for the time- intervalt = 5s to t = 10s v = 40-10/10-5 = 30/5 = 6 ms-1.
Related Solutions
The diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is
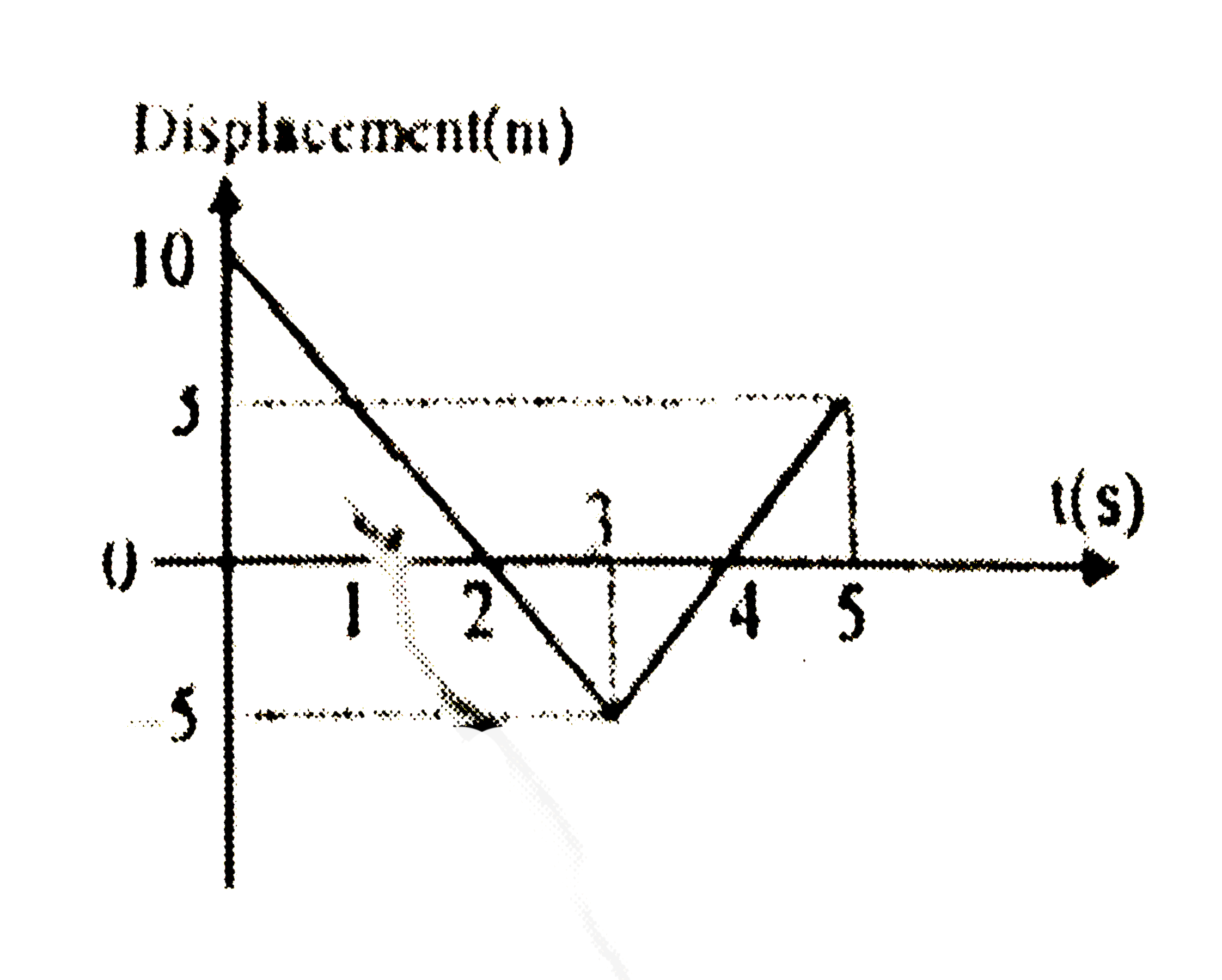
View SolutionThe diagram shows the displacement - time graph for a particle moving in a straight line. The distance (in m) coverted by the particle in the time interval t=0 to t=5s is

View SolutionThe acceleration of a particle varies with time t as a=t^(2)+t+2 where t is in seconds. The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in the figure. Mass of the particle is 2 kg. Work done by all the forces acting on the particle in time interval t = 0 to t = 10 sec is
View SolutionA particle is moving such that its position coordinates (x,y) are (2m,3m) at time t=0,(13m,14m) at time t=5s .Average velocity vector from t =0 to t=5s
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from to .
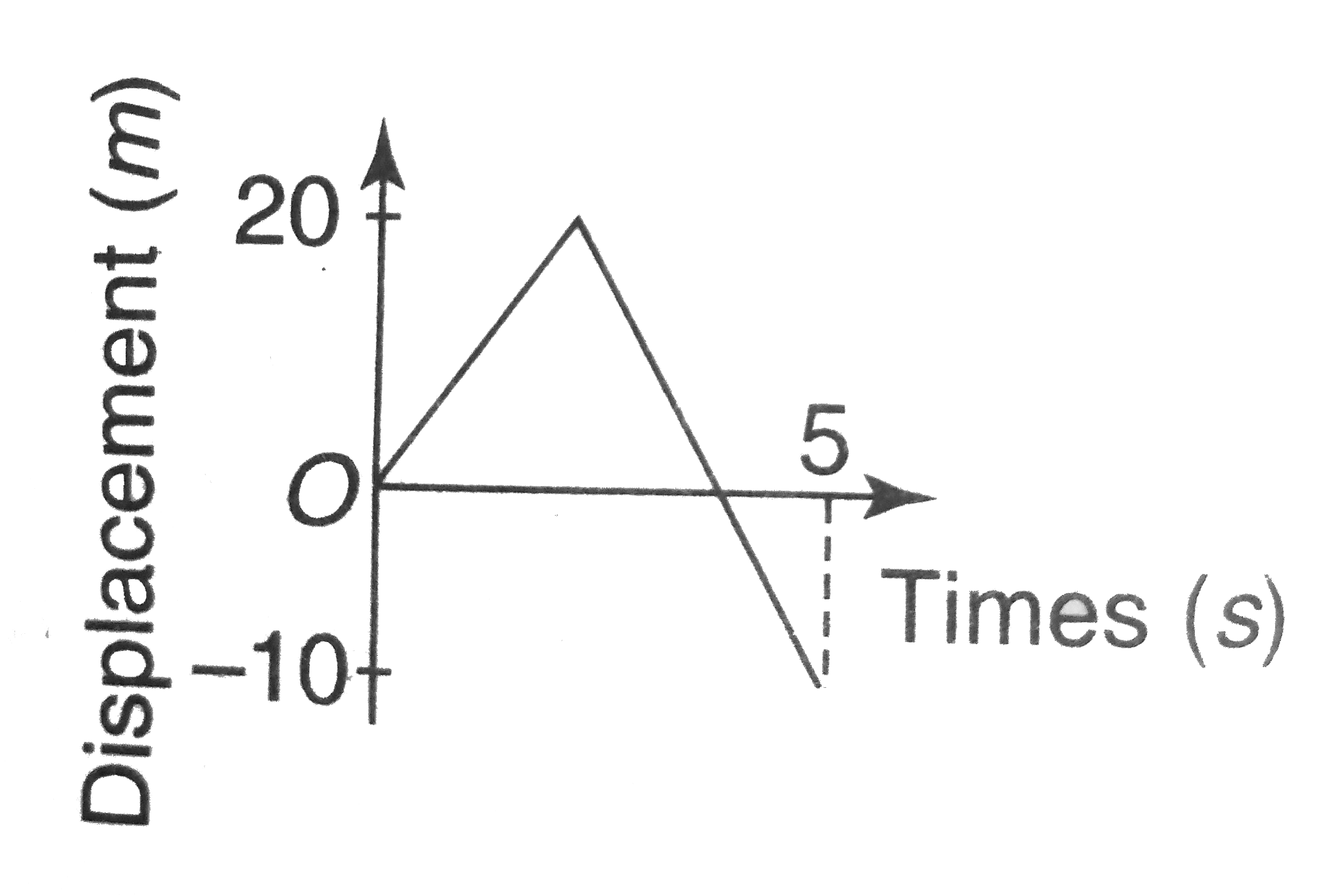
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from to .

View SolutionThe velocity time graph of a body moving in a straight line is shown. Find its (a) instantaneous velocity at t = 1.5 sec (b) average acceleration from t = 1.5 sec. to t = 2.5 sec (c) draw its acceleration time graph from t = 0 to t = 2.5 sec
View SolutionDuring one dimensional motion on x-axis Velocity time graph for particle is given.
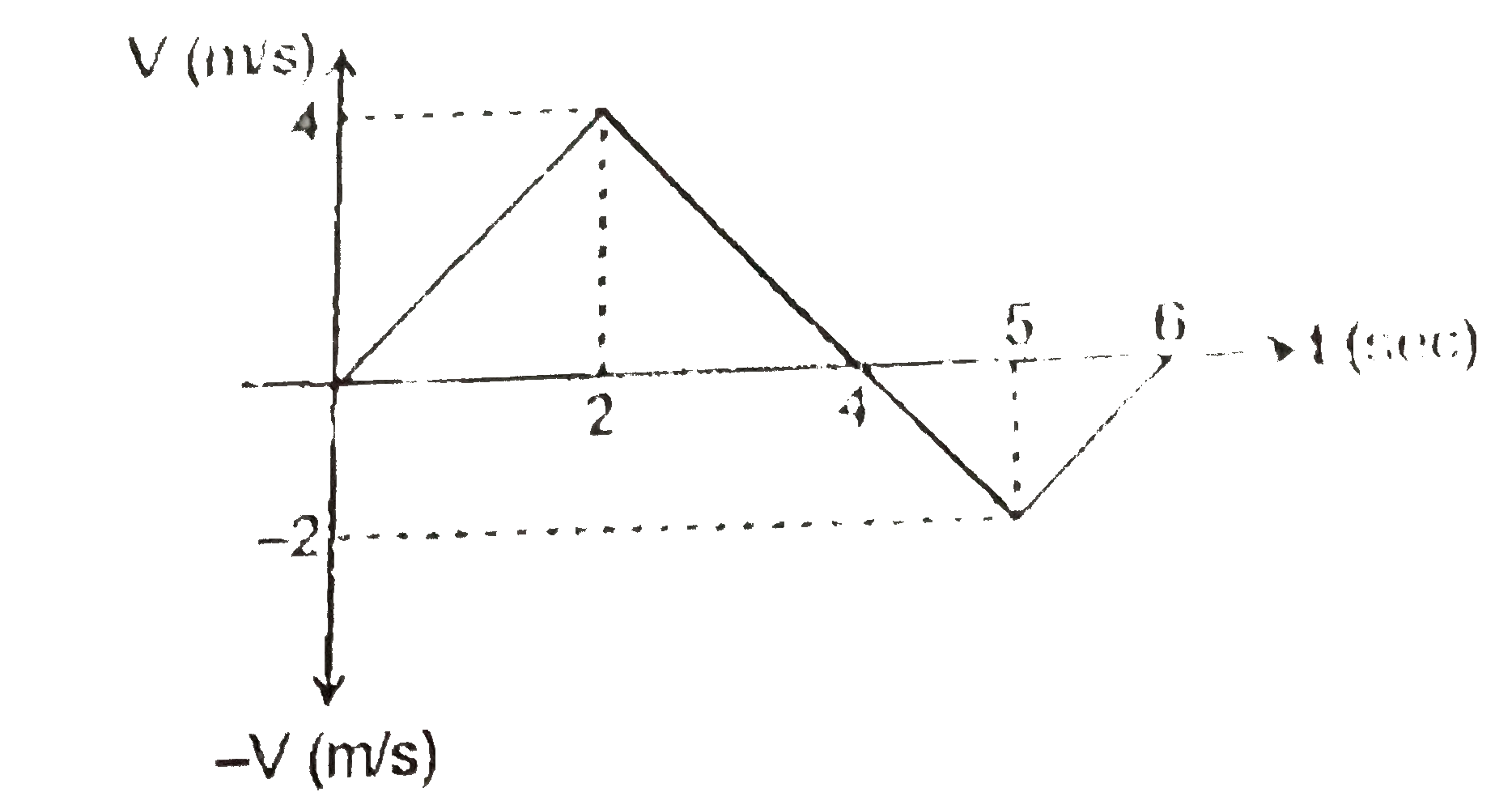
Average acceleration between (t = 0 sec) to (t = 6 sec)
View SolutionThe velocity-time graph of a body is given below. Find the average velocity from t = 0 to t = 40 s .
View Solutionvelocity-time graph of a particle moving in a straight line is as shown in figure. At time t = 0, velocity of the particle is zero. Find (a) average acceleration in a time interval from t = 6 s to t = 12 s, (b) velocity of the particle at t = 14 s.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from to find
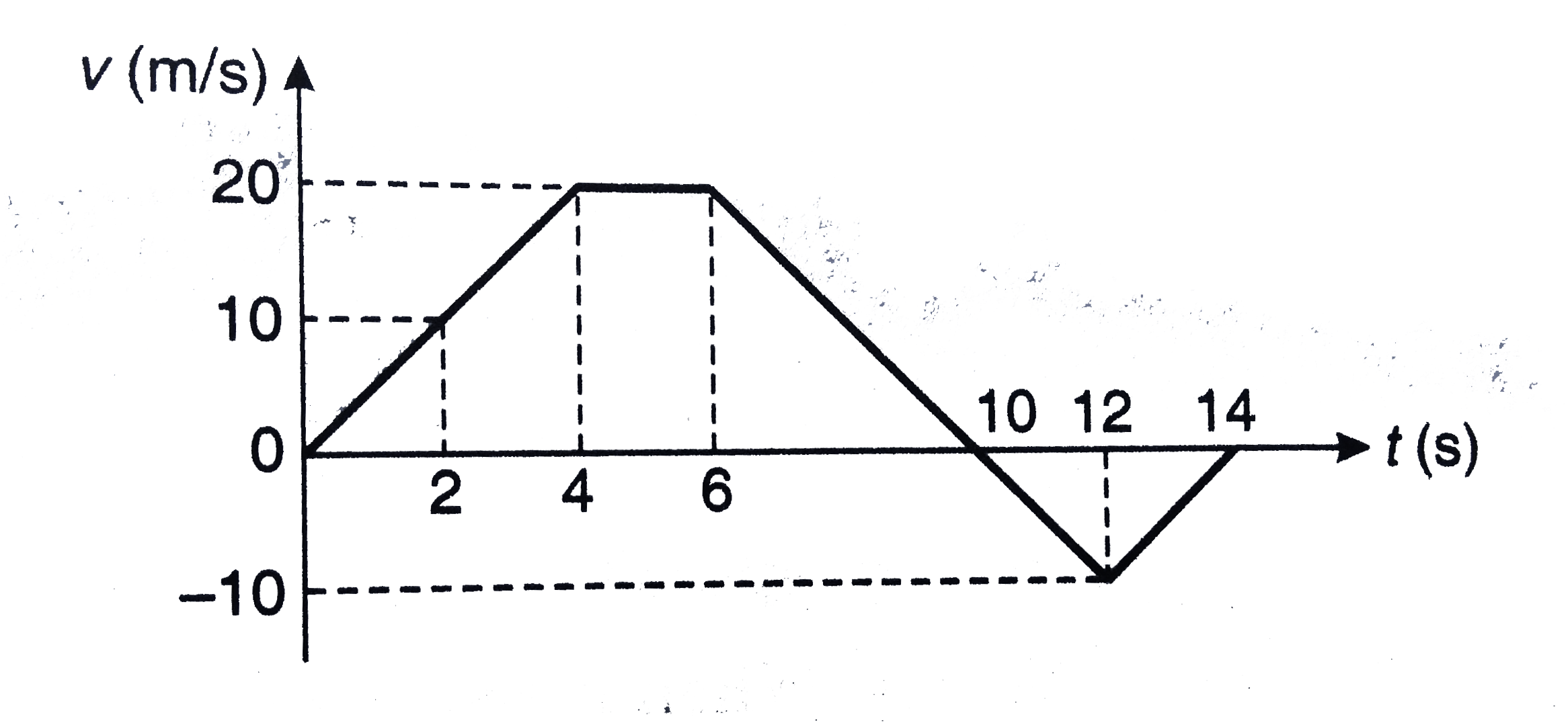
(a) average velocity and
(b) average speed of the particle.
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from to find
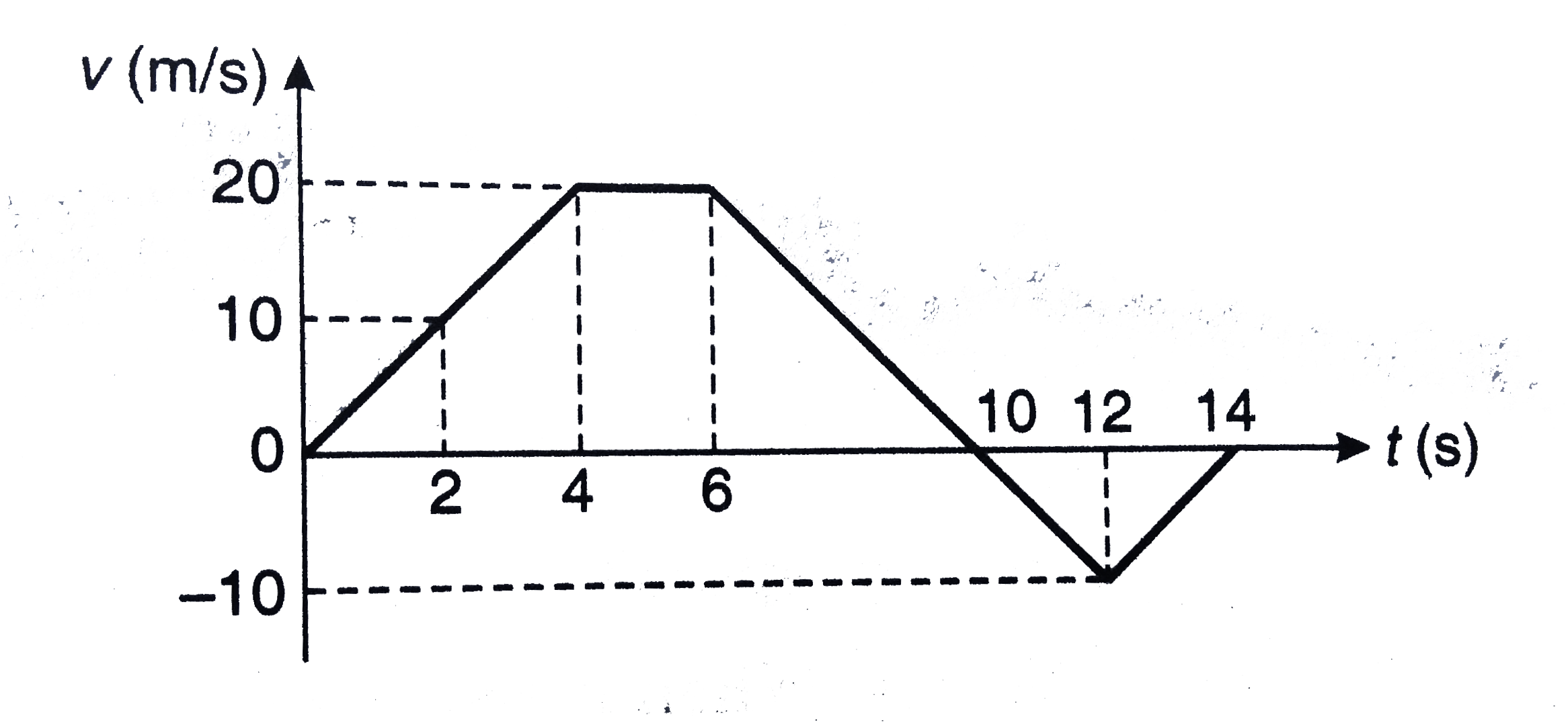
(a) average velocity and
(b) average speed of the particle.
View SolutionThe velocity of a particle is given by v=v_(0) sin omegat , where v_(0) is constant and omega=2pi//T . Find the average velocity in time interval t=0 to t=T//2.
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
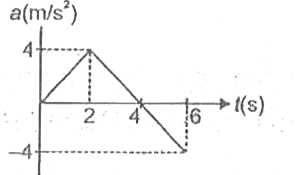
View SolutionAcceleration-time graph of a particle moving in a straight line is as shown in figure. At time t = 0, velocity of the particle is zero. Find (a) average acceleration in a time interval from t = 6 s to t = 12 s, (b) velocity of the particle at t = 14 s.
View SolutionVelocity of particle of mass 2kg varies with time t accoridng to the equation . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionVelocity of particle of mass 2kg varies with time t accoridng to the equation . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View SolutionVelocity of particle of mass 2kg varies with time t accoridng to the equation . Here t is in seconds. Find the impulse imparted to the particle in the time interval from t=0 to t=2s.
View Solution