The acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
To find the velocity of the particle at the end of 5 seconds given the acceleration function a(t)=t2+t+2 and the initial velocity v(0)=3m/s, we can follow these steps:
Step 1: Write the relationship between acceleration and velocity
Acceleration a is the rate of change of velocity v with respect to time t:
a=dvdt
Substituting the given acceleration function, we have:
dvdt=t2+t+2
Step 2: Rearrange the equation for integration
Rearranging the equation gives:
dv=(t2+t+2)dt
Step 3: Integrate both sides
We will integrate both sides. The left side will be integrated with respect to v, and the right side with respect to t:
∫dv=∫(t2+t+2)dt
This results in:
v=t33+t22+2t+C
where C is the constant of integration.
Step 4: Determine the constant of integration
To find C, we use the initial condition v(0)=3:
v(0)=033+022+2(0)+C=3
Thus, C=3. Therefore, the equation for velocity becomes:
v(t)=t33+t22+2t+3
Step 5: Calculate the velocity at t=5 seconds
Now, we substitute t=5 into the velocity equation:
v(5)=533+522+2(5)+3
Calculating each term:
- 533=1253
- 522=252
- 2(5)=10
Putting it all together:
v(5)=1253+252+10+3
Step 6: Find a common denominator and simplify
The common denominator for 3 and 2 is 6:
- Convert 1253 to 2506
- Convert 252 to 756
- Convert 10 to 606
- Convert 3 to 186
Now we can combine:
v(5)=250+75+60+186=4036
Step 7: Final calculation
Calculating 4036 gives approximately:
v(5)≈67.167m/s
Final Answer
The velocity of the particle at the end of 5 seconds is approximately 67.167m/s.
Acceleration a is the rate of change of velocity v with respect to time t:
a=dvdt
Substituting the given acceleration function, we have:
dvdt=t2+t+2
Rearranging the equation gives:
dv=(t2+t+2)dt
We will integrate both sides. The left side will be integrated with respect to v, and the right side with respect to t:
∫dv=∫(t2+t+2)dt
This results in:
v=t33+t22+2t+C
where C is the constant of integration.
To find C, we use the initial condition v(0)=3:
v(0)=033+022+2(0)+C=3
Thus, C=3. Therefore, the equation for velocity becomes:
v(t)=t33+t22+2t+3
Now, we substitute t=5 into the velocity equation:
v(5)=533+522+2(5)+3
Calculating each term:
- 533=1253
- 522=252
- 2(5)=10
v(5)=1253+252+10+3
The common denominator for 3 and 2 is 6:
- Convert 1253 to 2506
- Convert 252 to 756
- Convert 10 to 606
- Convert 3 to 186
v(5)=250+75+60+186=4036
Calculating 4036 gives approximately:
v(5)≈67.167m/s
The velocity of the particle at the end of 5 seconds is approximately 67.167m/s.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:PRACTICE PROBLEMS
Explore 28 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CONCEPTUAL QUESTIONS
Explore 14 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
The acceleration a in ms−2 of a particle is given by a=3t2+2t+2, where t is the time. If the particle starts out with a velocity v=2ms−1 at t=0, then find the velocity at the end of 2s.
View SolutionThe acceleration a in ms−2 of a particle is given by a=3t2+2t+2, where t is the time. If the particle starts out with a velocity v=2ms−1 at t=0, then find the velocity at the end of 2s.
View Solution
Knowledge Check
Power supplied to a particle of mass 2 kg varies with time as P=3t22W, where t is in seconds. If velocity of particle at t=0 is zero, then the velocity of particle at t=2 s will be
A1 m s−1B4 m s−1C2ms−1D2√2ms−1Power supplied to a particle of mass 2 kg varies with time as P=3t22, where t is in seconds. If velocity 2 of particle at t = 0 is v = 0, the velocity of particle at t = 2 s will be
A1m/sB4m/sC2m/sD272m/sThe acceleration of a particle is increasing linearly with time t as bt. The particle starts from the origin with an initial velocity v0. The distance travelled by the particle in time t will be
Av0t+16bt3Bv0t+13bt3Cv0t+13bt2Dv0t+12bt2
The acceleration a in "m/s^(2)" of a particle is given by,a=3t^(2)+2t+2 where t is the time.If the particle starts out with a velocity u=2m/s at t=0then the velocity at the end of 2 second is
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
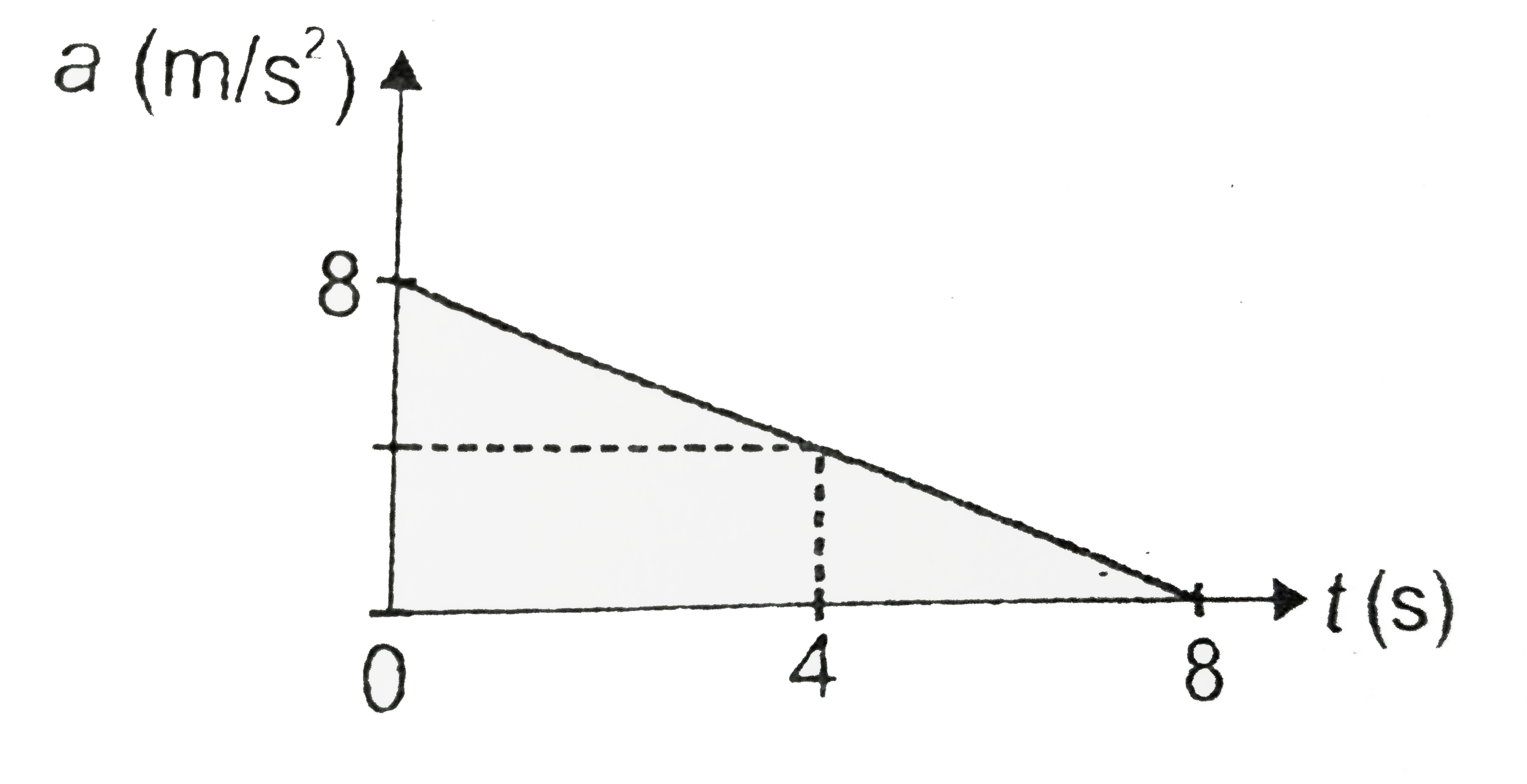
View SolutionPower supplied to a particle of mass 2kg varies with time asP=3t22 watt,where t is in seconds If velocity of particle at t=0 is v=0 the velocity of particle at t=2 sec will be ?
View SolutionThe acceleration of a particle is increasing linearly with time t as bt .The particle starts from the origin with an initial velocity v_(0) The distance travelled by the particle in time t will be
View SolutionThe acceleration of paticle varies with time as :
a(t)=3t2+4
If the initial velocity of particle is 2m/s, find the velocity of particle at t=3sec.
View Solution

