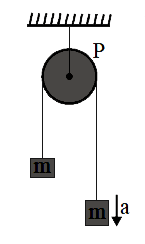
In the figure the disc D does not slip on the surface S. The pulley P has mass and the string does not slip on it. The string is wound around the disc.a The acceleration of the block B is double the acceleration of the centre of D. b The force of friction exerted by D on S acts to the left. c The horizontal and the vertical sections of the string have the same tension. d The sum of the kinetic energies of D and B is less than the loss in the potential energy of B as it moves down.
Correct Answer is: a b & dAlso the rotating pulley has some kinetic energy derived from the loss in potential energy of the block B as it moves down.
Related Solutions
In the figure, the disc D does not slip on the surface S , the pulley P has mass and the string does not slip on it. The string is wound around the disc.
View SolutionA mass m hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, the acceleration of the mass m if the string does not slip on the pulley, is
View SolutionAn object of mass is tied to a light string wound around a pulley that has a moment of inertia and radius . The wheel bearing is fricrtionless and the string does not slip on the run. Find the tension in the string and the acceleration of the object.
View SolutionFigure shows two blocks of mass m and m connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley (uniform disc) has mass m and it can freely rotate about this axis. Find the acceleration of the mass m assuming that the string does not slip on the pulley.
View SolutionIn the figure, the blocks unequal masses and (). has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
View Solution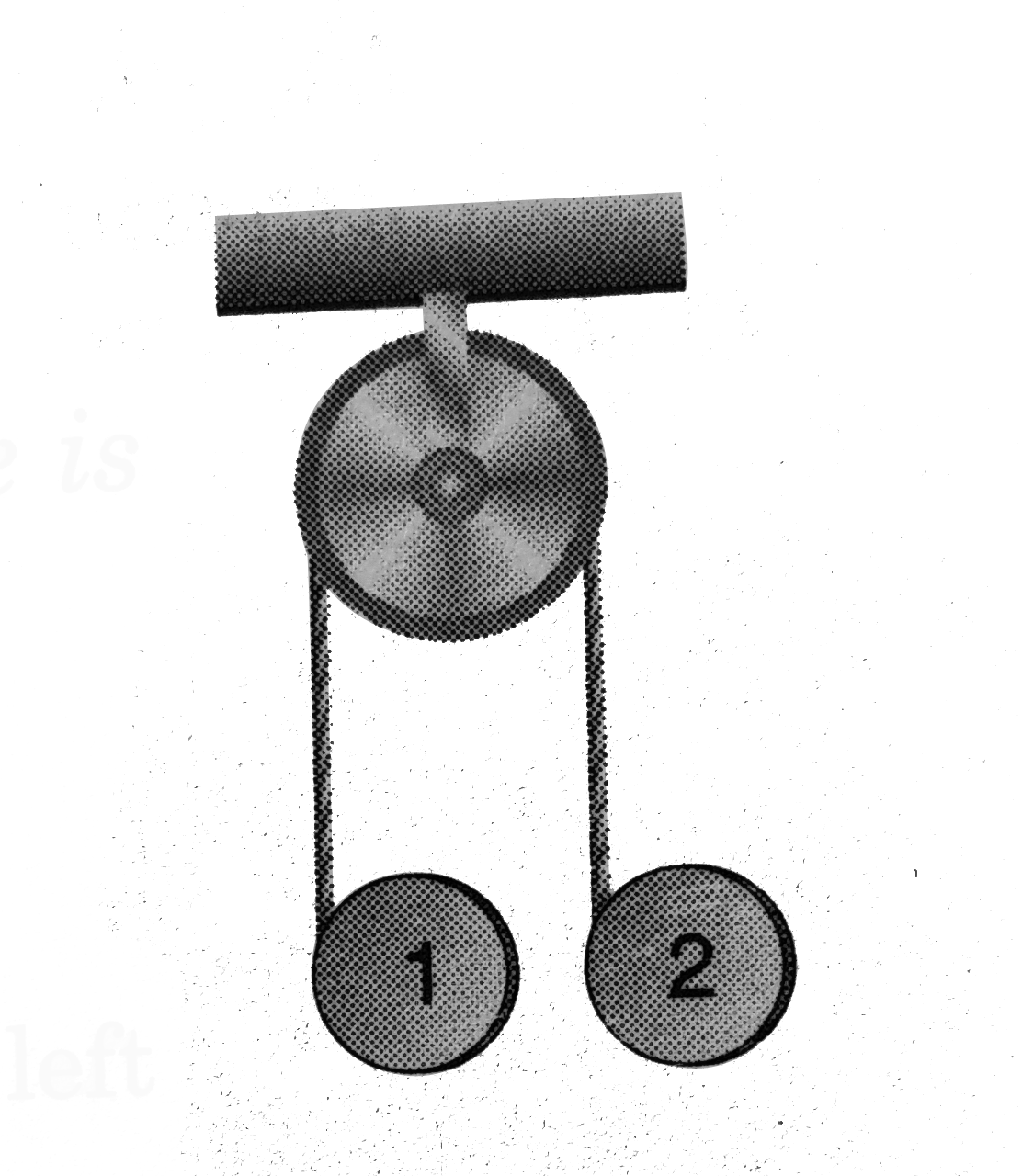
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.
View SolutionA thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.
View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionConsider4 the situation shown in figure. Bothe the pulleys and the string are light and all the surfaces are friction less. a. Find the acceleration of the mass M. b. Find the tension in the string c. Calculate the force exerted by the clamp on the pulley A in the figure.

View SolutionA string of mass m is hung around a pulley on a yearless cheering, the mass of the pulley is m and the radius is. Assume that the pulley is a perfect uniform circular wheel if the string does not slip on the pulley. Then the acceleration of the mass m is
View SolutionIn the given figure two blocks of unequal mass m_(1) And m_(2) ( m_(1) lt m_(2)) Is. m_(2) The downward acceleration of a is pulley P has radius r and some mass. The string does not slip on the pulley. Find the acceleration of the block and the angular acceleration of the pulley (I = moment of inertia of pulley)
View SolutionTwo blocks are connected by a string that passes over a pulley of radius and moment of inertia . The block of mass sides on a frictionless, horizontal surface, the block of mass is suspended from the string. Find the acceleration of the blocks and the tension and assuming that the string does not slip on the pulley.

View SolutionConsider the situation shown in figure. Both the pulleys and the strings are light and all the surfaces are frictionless. Calculate
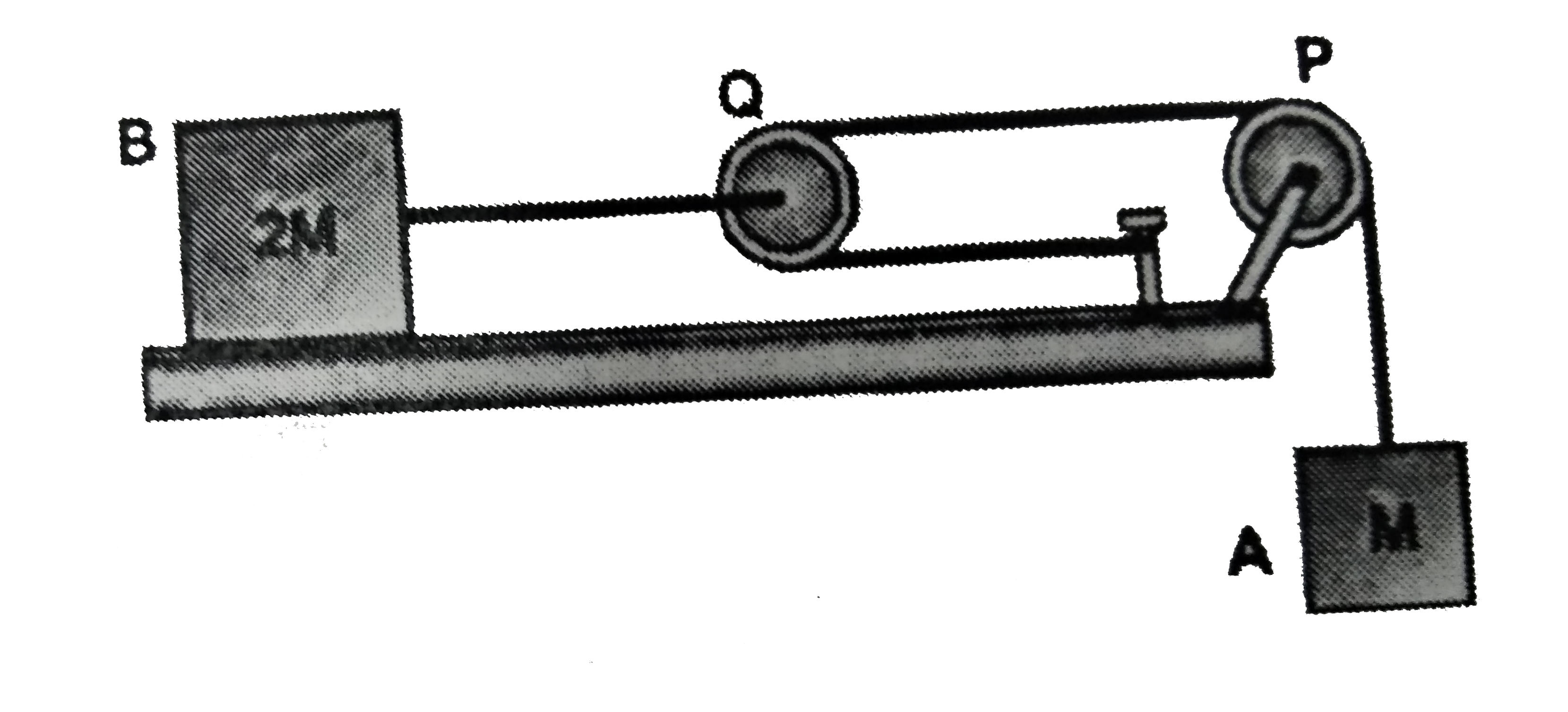
(a) the acceleration of mass M,
(b) tension in the string PQ and
(c ) force exerted by the pulley P.
View SolutionConsider the situation shown in figure. Both the pulleys and the strings are light and all the surfaces are frictionless. Calculate

(a) the acceleration of mass M,
(b) tension in the string PQ and
(c ) force exerted by the pulley P.
View Solutionएक घर्षणहीन बेयरिंग पर एक घिरनी के चारों ओर एक डोरी को लपेट कर द्रव्यमान m लटकाया गया है। घिरनी का द्रव्यमान m और त्रिज्या R है। यह मान लें कि घिरनी एक पूर्ण एकसमान वृतीय चकती है। यदि डोरी घिरनी पर फिसलती नहीं है, तब द्रव्यमान m का त्वरण है
View SolutionA mass m hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, what is the acceleration of the mass m, if the string does not slip on the pulley.
View SolutionA mass m hangs with the help of a string wrapped around a pulley on a frictionless bearing. The pulley has mass m and radius R. Assuming pulley to be a perfect uniform circular disc, what is the acceleration of the mass m, if the string does not slip on the pulley.
View SolutionA block of mass is attached at the end of an inextensible string which is wound over a rough pulley of mass and radius figure a. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
View SolutionIn the arrangement shown in figure, m_A = m_B = 2kg. String is massless and pulley is frictionless. Block B is resting on a smooth horizontal surface, while friction coefficient beteen block A and B is . the Maximum horizontal force F that can be applied so that block A does not slip over block B is.

View SolutionIn the figure and are two blocks of mass and respectively attached to the two ends of light string passing overa disc of mass and radius . The disc is free to rotate about a fixed horizontal the string does not string does not slip over the disc. Find.
(i) The linear acceleration of mass .
(ii) the number of revolutions made by the disc at the end of . from the start.
(iii) the tension in teh string segment supporting the block .
 .
.
View Solution