
A thread is wound around two discs on either sides. The pulley and the two discs have the same mass and radius. There is no slipping at the pulley and no friction at the hinge. Find out the acceleration of the two discs and the angular acceleration of the pulley.



Let R be the radius of the disc and T1 and T2 be the tensions in the left and right segments of the rope
Acceleration of disc 1,
a1=mg−T1m ..(i)
Acceleration of disc 2, a2=mg−T2m ..(ii)
Angular acceleration of disc 1, α1=τI=T1R12mR2=2T1mR ..(iii)
Similarly, angular acceleration of disc 2, α2=2T2mR ..(iv)
Both α1 and α2 are clockwise.
Angular acceleration of pulley
α=(T2−T1)R12mR2=2(T2−T1)mR ..(v)
For no slipping Ra1=a2−Rα2=Rα ..(vi)
Solving these equation we get
a=0 and a1=a2=2g3
Alternate solution
As both the discs are in identical situation T1=T2 and α=0 i.e, each of the discs falls independently and identically. therefore this is exactly similar to the problem shown in figure.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Solved Example
Explore 1 Video
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.1
Explore 10 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Solved Examples
Explore 25 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
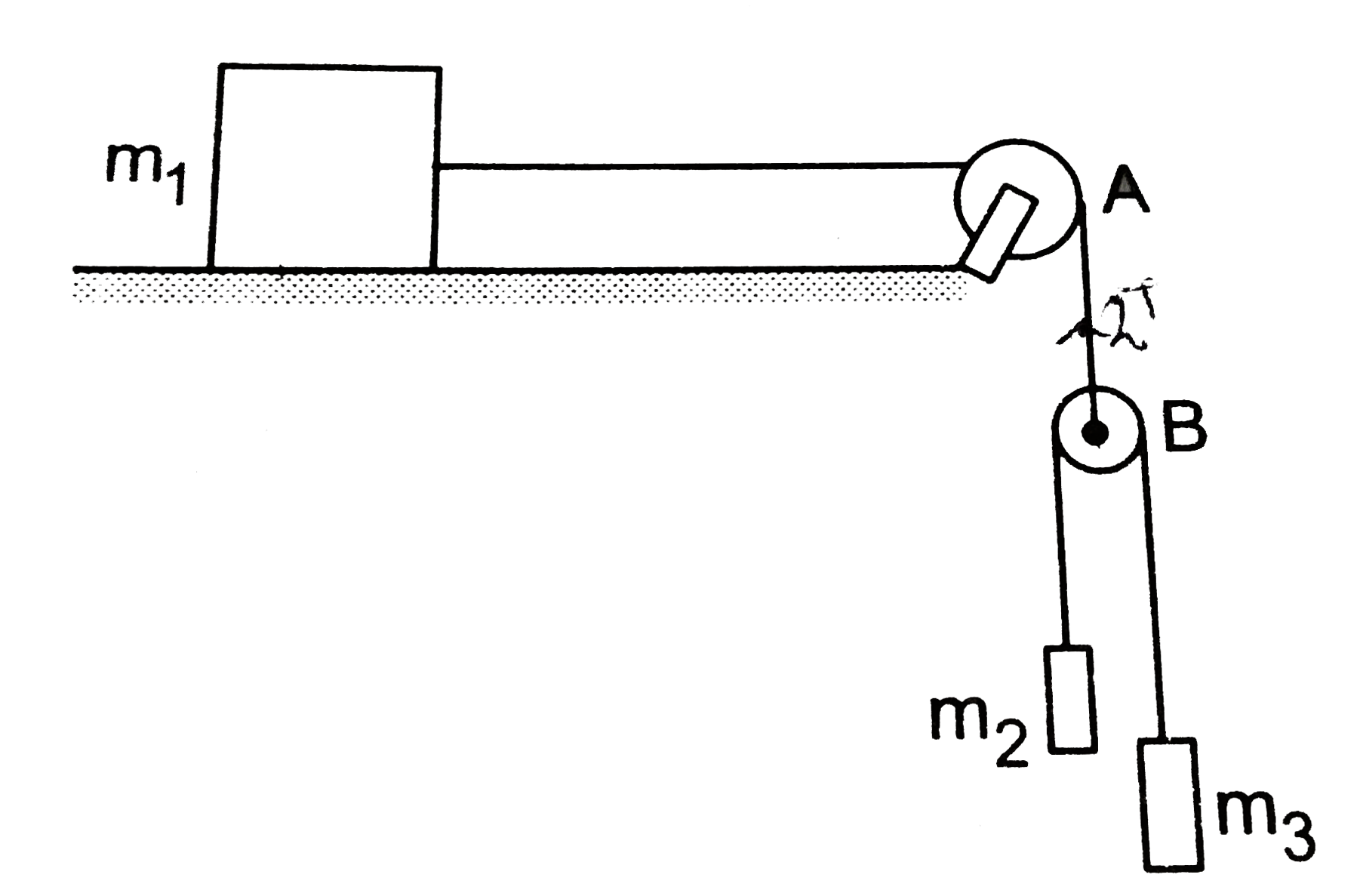
Three blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View SolutionA uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

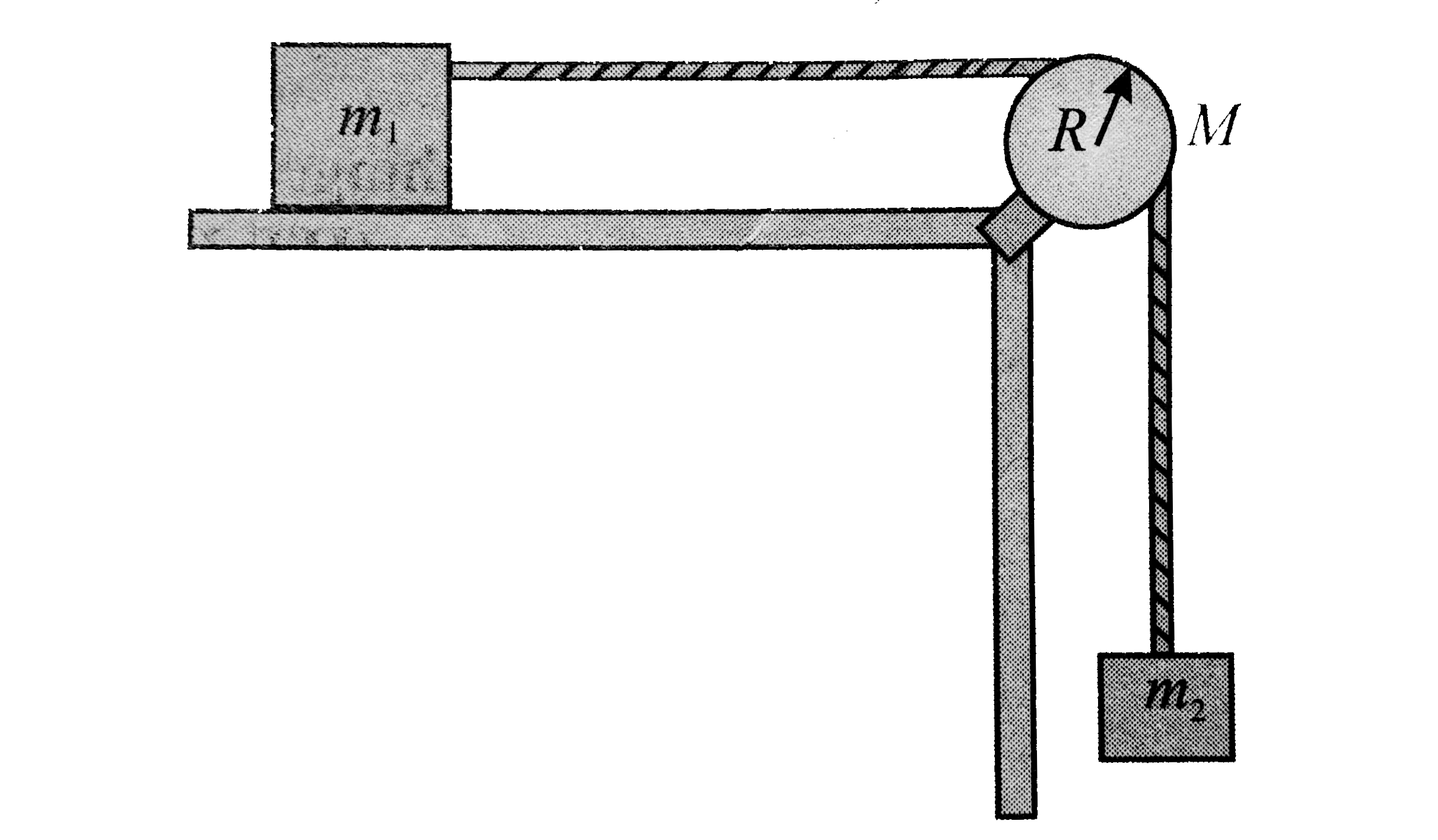
View SolutionIn figure mass m1 slides without friction on the horizontal surface, the frictionless pulley is in the form of a cylinder of mass M and radius R, and a string turns the pulley without slipping. Find the acceleration of each mass, and tension in each part of the string.
View SolutionTwo equal and opposite forces F are allplied tangentially to a uniform disc of mass M and radius R . If the disc is pivoted at its centre and free to rotate in its plane, the angular acceleration of the disc is :
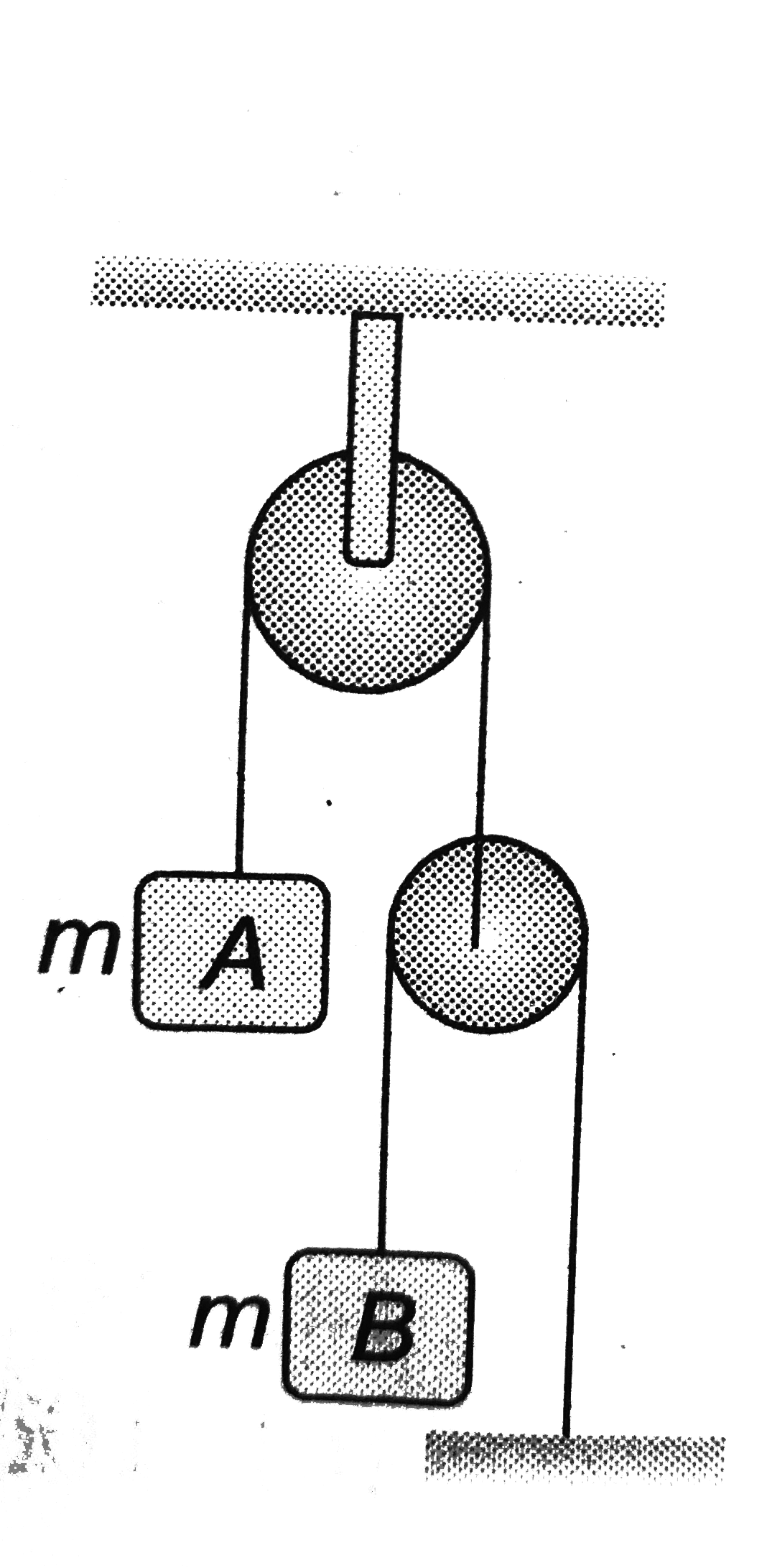
View SolutionIn the figure shown neglecting friction and mass of pulley, what is the acceleration of mass B ?
View Solution
In the arrangement shown in figure the mass of the uniform solid cylindrical pulley of radius R is equal to m and the masses of two bodies are equal to m1 and m2. The thread slipping and the friction in the axle of the pulley are supposed to be absent. Find the angular acceleration of the cylinder and the ratio of tensions T1T2 of the vertical sections of the thread in the process of motion.
View SolutionA disc shaped pulley of mass 'm'=4kg and radius R=0.5m can rotate freely about its center. A block of mass M=2kg hangs from the pulley through is massless string that is tightly wrapped around the pulley. When the system is released, there is no slipping between pulley and string.
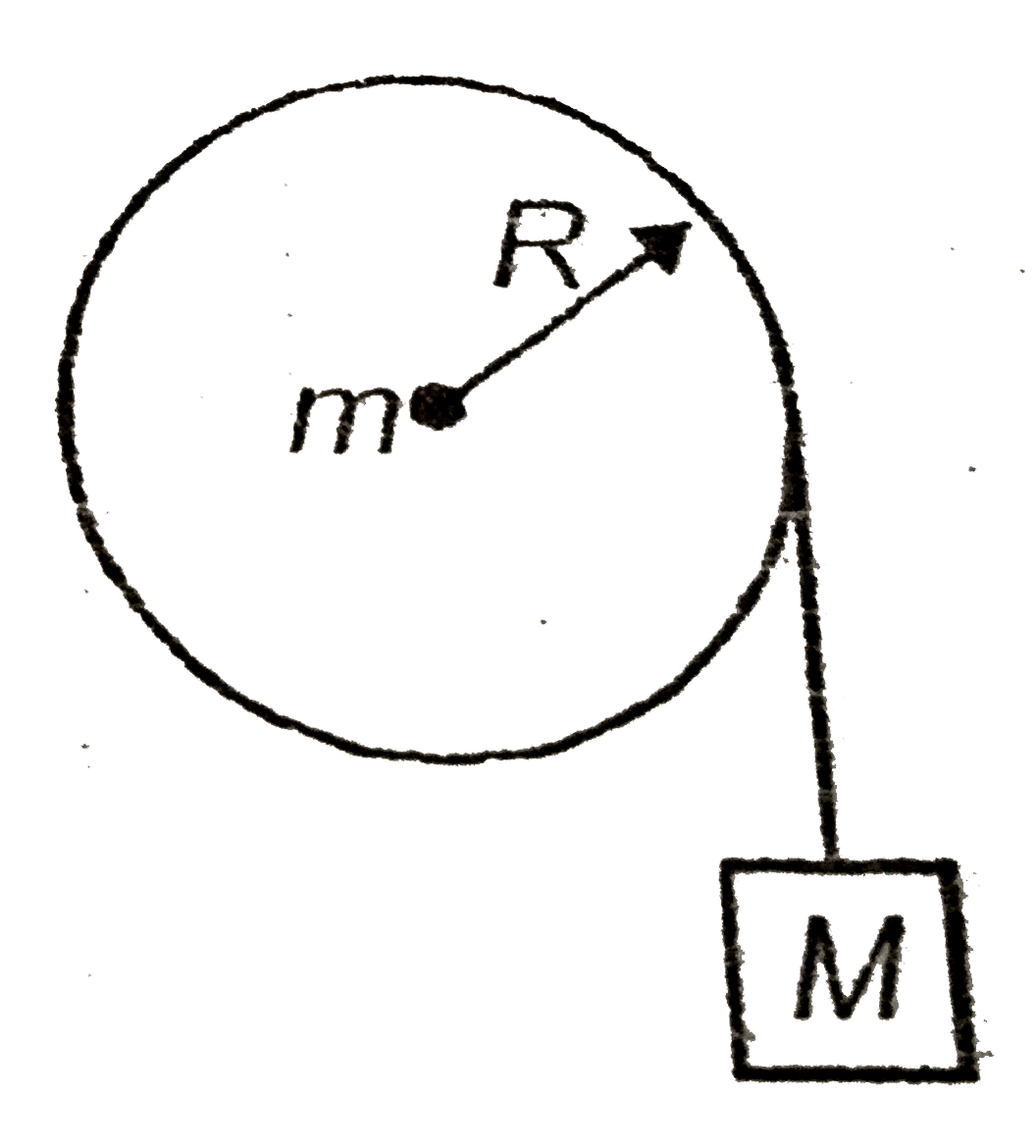
(a) Calculate the angular accelerating of the pulley
(b) Calculate the tension in the string
View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
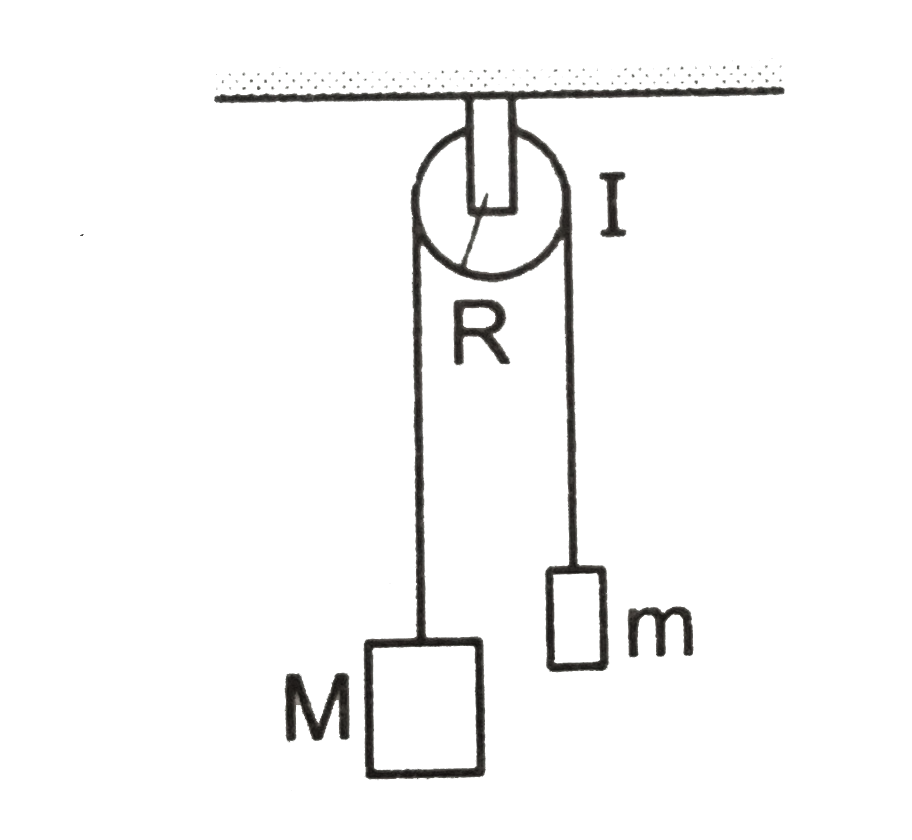
View SolutionA pulley is attached to the celing of a lift moing upwards. Two particles are attached to the two ends of a stirng passing over the pulley. The masses of the particles are in the ration 2:1 if the acceleration of the particles is g/2, then the acceleration of the lift will be
View SolutionTwo blocks of same mass 'm' are connected by the cable passing over a pulley of mass 'm' and radius 'R'. There is no slipping between the pulley and the cable. The coefficient of friction between the block 'A' and the horizontal surface is 1/4 . At the moment shown in the figure,the tension in the cable AB is
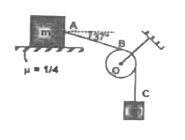
View Solution

