Find the greatest and least moment of inertia of an inverted T–section shown in fig.
Since diagram is symmetrical about y axis i.e. X = 0 x1 = x2 = 0 A1 = 5 × 20 = 100cm2 A2 = 15 × 5 = 75cm2 y1 = 5 + 20/2 = 15cm y2 = 5/2 = 2.5cm Y = A1y1 + A2y2/A1 + A2 = 100 × 15 + 75 × 2.5/100 + 75 = 9.64 cm C.G. = 0 9.64 Moment of inertia M.I. about x-x axis = IXX = IXX1 + IXX2 IXX1 = IGXX1 + A1h12 = bd3/121 + A1Y – y12 = 5 × 203/12 + 5 × 20 9.64 – 152 = 6206.09 cm4 ...i IXX2 = IGXX2 + A2h22 = bd3/122 + A2Y – y22 = 15 × 53/12 + 15 × 5 9.64 – 2.52 = 3979.72 cm4 ...ii IXX = IXX1 + IXX2 = 6206.09 + 3979.72 = 10186.01 cm4 ...iii Moment of inertia M.I. about y-y axis = Iyy = Iyy1 + Iyy2; h = 0 Since X = 0 i.e.; X1 = X2 = 0 Iyy1 = IGyy1 + A1h12 = db3/121 + A1X – X12 = db3/121 Iyy2 = IGyy2 + A2h22 = db3/122 Iyy = Iyy1 + Iyy2 = 20 × 53/12 + 5 × 153/12 = 1614.25 cm4 ...iv Greatest Moment of inertia = IXX = 10186.01 cm4
Related Solutions
चित्र में दर्शाए अनुसार M द्रव्यमान व L लम्बाई की एक एकसमान छड़ जो एक अक्ष से कोण पर है, का जड़त्व आघूर्ण ज्ञात कीजिए।
View SolutionFind the moment of inertia of solid sphere of mass M about a diameter as shown in Fig.
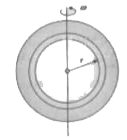
View SolutionThree rings, each of mass and radius , are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.
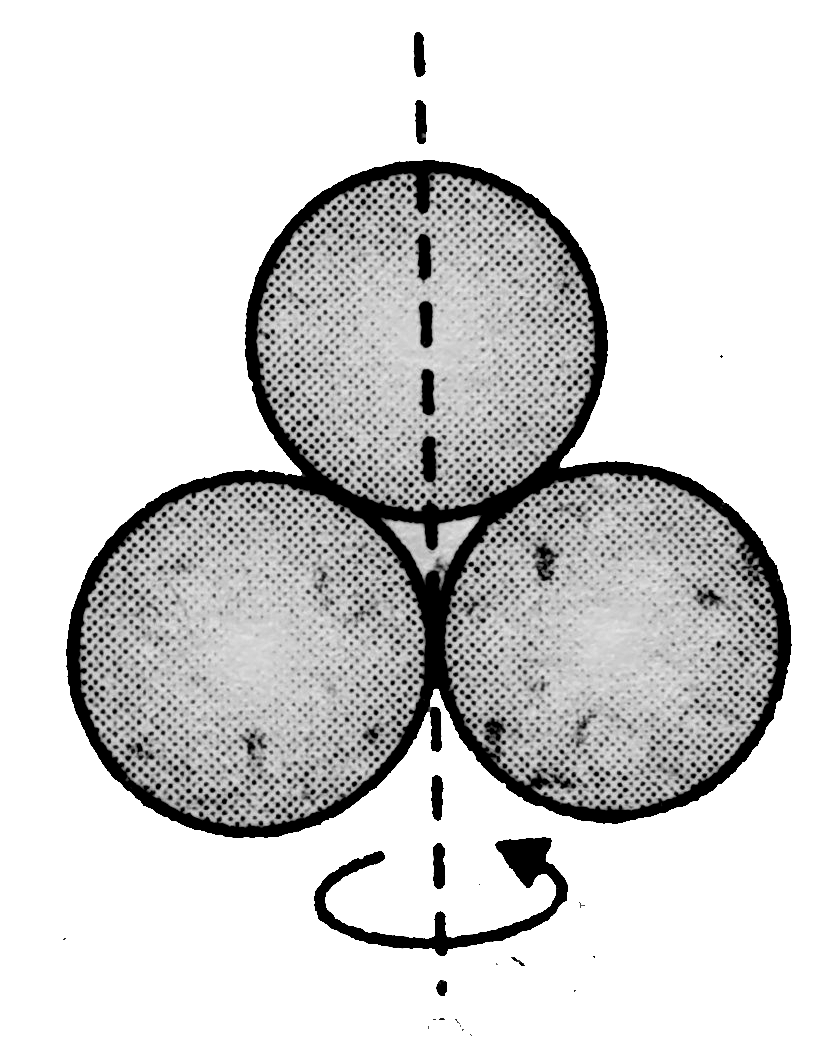
View SolutionFind the moment of inertia of the two uniform joint rods about point as shown in Fig. Use parallel axis theorem. Mass of each rod is .
View SolutionThree rings, each of mass and radius , are so placed that they touch each other. Find the moment of inertia about the axis as shown in Fig.

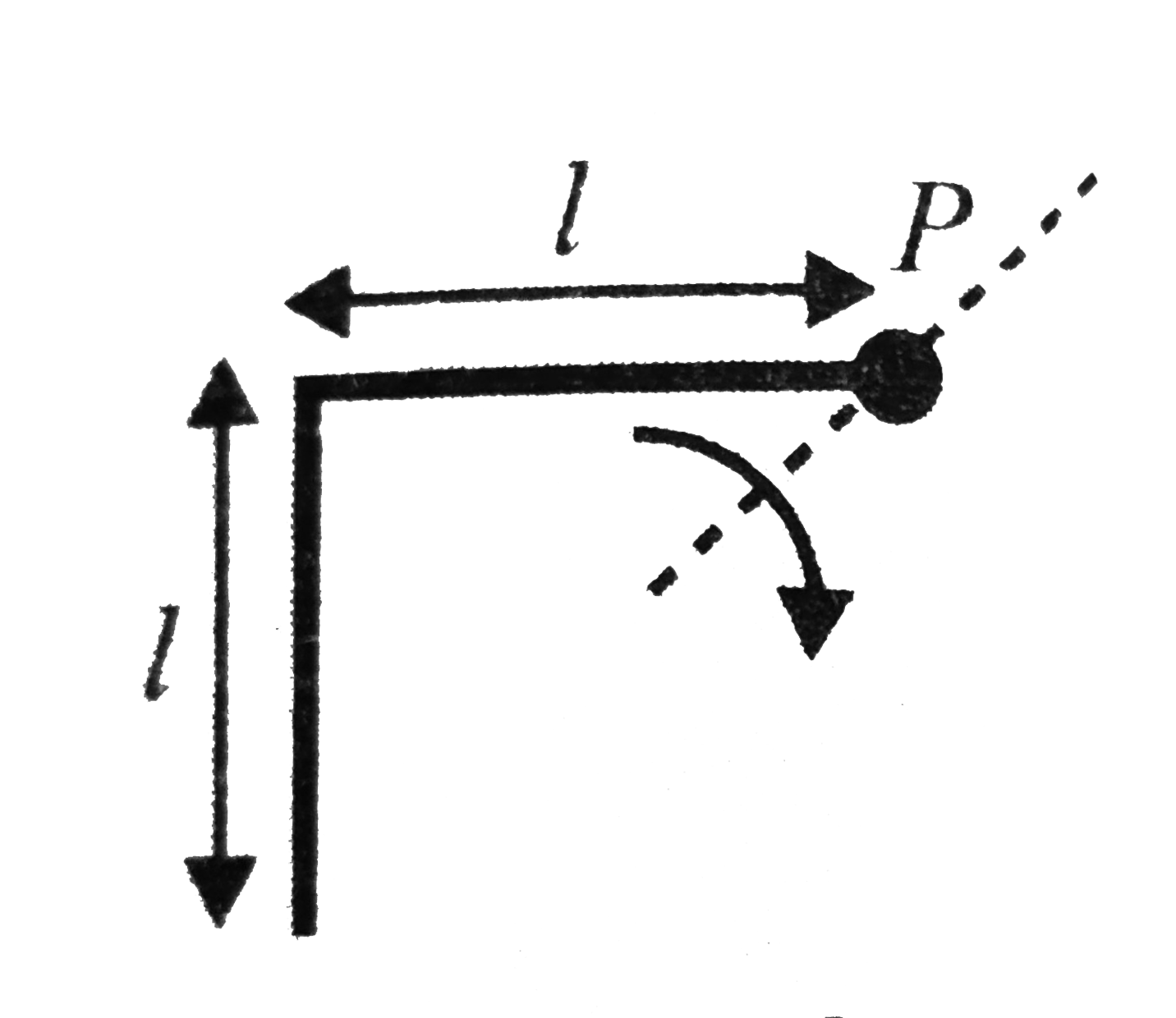
View SolutionFind the moment of inertia of the two uniform joint rods about point P as shown in Fig. Use parallel axis theorem. Mass of each rod is M .
View SolutionFind moment of inertia of a uniform rectangular plate about axis zz' passing through center and perpendicular to the plane of plate, as shown in Fig.
View SolutionThree identical rings of masses m each and radius r are kept in contact as shown in Fig. Find the moment of inertia of the system about a common tangent.
View SolutionFind the moment of inertia about the rotation axis XX 'in the pictures shown.
View SolutionFind the moment of Inertia of a cuboid along the axis as shown in the figure.
View Solutionदिखाए गये चित्रों में घूर्णन अक्ष XX ' के परितः जड़त्व आघूर्ण ज्ञात कीजिये ।
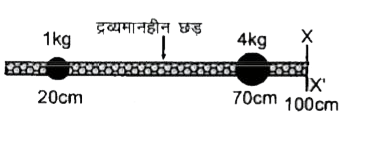
View Solutionदिखाए गये चित्रों में घूर्णन अक्ष XX ' के परितः जड़त्व आघूर्ण ज्ञात कीजिये ।

View Solutionनिम्न व्यवस्थाओ में दर्शायी अक्ष XX' के सापेक्ष जड़त्व आघूर्ण ज्ञात करो।

View Solutionनिम्न व्यवस्थाओ में दर्शायी अक्ष के सापेक्ष जड़त्व आघूर्ण ज्ञात करो।

View SolutionCalculate the moment of inertia of a rod of mass 2 kg and length 0.5 m in each of the following cases, as shown in Fig. 8.52.
View SolutionThe moment of inertia of a sphere about its diameter is I. Four such circles are arranged as shown in the figure. Find the moment of inertia of the system about the XX axis.
View SolutionFind the moment of inertia of a section of circular disc of radius R about an axis perpendicualr to its plane as shown in the figure. The section has mass m and subtends an angle at the centre.
View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over of the edge of the square as shown in fig. p-10. The side of the square is 2a. The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma^2 . The moment of inertia of the lamina is ......
View SolutionCalculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.

View SolutionCalculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.
View Solution