Find moment of inertia of a uniform rectangular plate about axis zz' passing through center and perpendicular to the plane of plate, as shown in Fig.

To understand the motion of plate, imagine twirling your note book about its center by keeping index finger of two hands on two faces of the note book.
Calculations: This is a simple problem that can be solved using theorem of perpendicular-axis.
Compute: From Fig. , we see that
Ixx.=Mb212andIxx.=Ml212.

Hence, from theorem of perpendicular-axis
Izz.=Ixx.+Iyy.
= M(B2+l212).
Topper's Solved these Questions
- RIGID BODY DYNAMICS - IBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS - IExercise:CHECKPOINT
Explore 18 Videos
- RIGID BODY DYNAMICS - IBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS - IExercise:PROBLEMS
Explore 100 Videos
- RELATIVITYBook:RESNICK AND HALLIDAYChapter:RELATIVITYExercise:PRACTICE QUESTIONS (Integer Type)
Explore 5 Videos
- RIGID BODY DYNAMICS-IIBook:RESNICK AND HALLIDAYChapter:RIGID BODY DYNAMICS-IIExercise:PRACTICE QUESTIONS (Integer Type)
Explore 2 Videos
Similar Questions
Derive an expression for moment of inertia of a thin circular ring about an axis passing through its centre and perpendicular to the plane of the ring.
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctThe moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is
A(MR2B32MR[^(2)CMR22D54MR2Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2
(i) Consider an infinitesimally thin triangular strip having mass M and length L. Find the moment of inertia of the strip about on axis passing through its tip and perpendicular to the plane. Compare the result with moment of inertia of a uniform disc of mass M and radius L about an axis passing through its centre and perpendicular to the plane the disc. Why the two expressions are same?

(ii) A circular fan made of paper is in shape of a disc of radius R. The fan can be folded (various stages shown in figure (a) through (f)) to the shape of a thin stick. The moment of inertia of the circular fan about an axis passing through centre O and perpendicular to the plane of the figure is I0=12MR2 where M= mass of the fan.

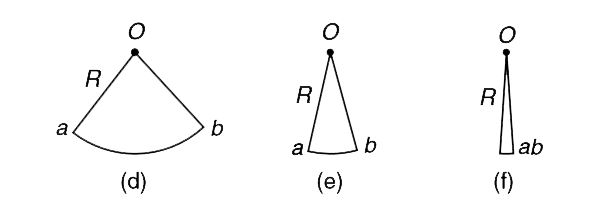
(a) How does the moment of inertia (I), about an axis perpendicular to the plane of the figure passing through O, change as the fan is folded through stage a to b to c to d to e?
(b) When the fan is completely folded in the shape of a stick (fig. (f)), write its moment of inertia about the above mentioned axis.
Note : Moment of inertia of a uniform rod about an axis through its end and perpendicular to it is ML23
View SolutionMoment of inertia of a square plate of side l about the axis passing through one of the corner and perpendicular to the plane of square plate is given by :
View SolutionMoment of inertia of a rectangular plate about an axis passing through P and perpendicular to the plate is I. Moment of PQR about an axis perpendicular to the plane of the plate :
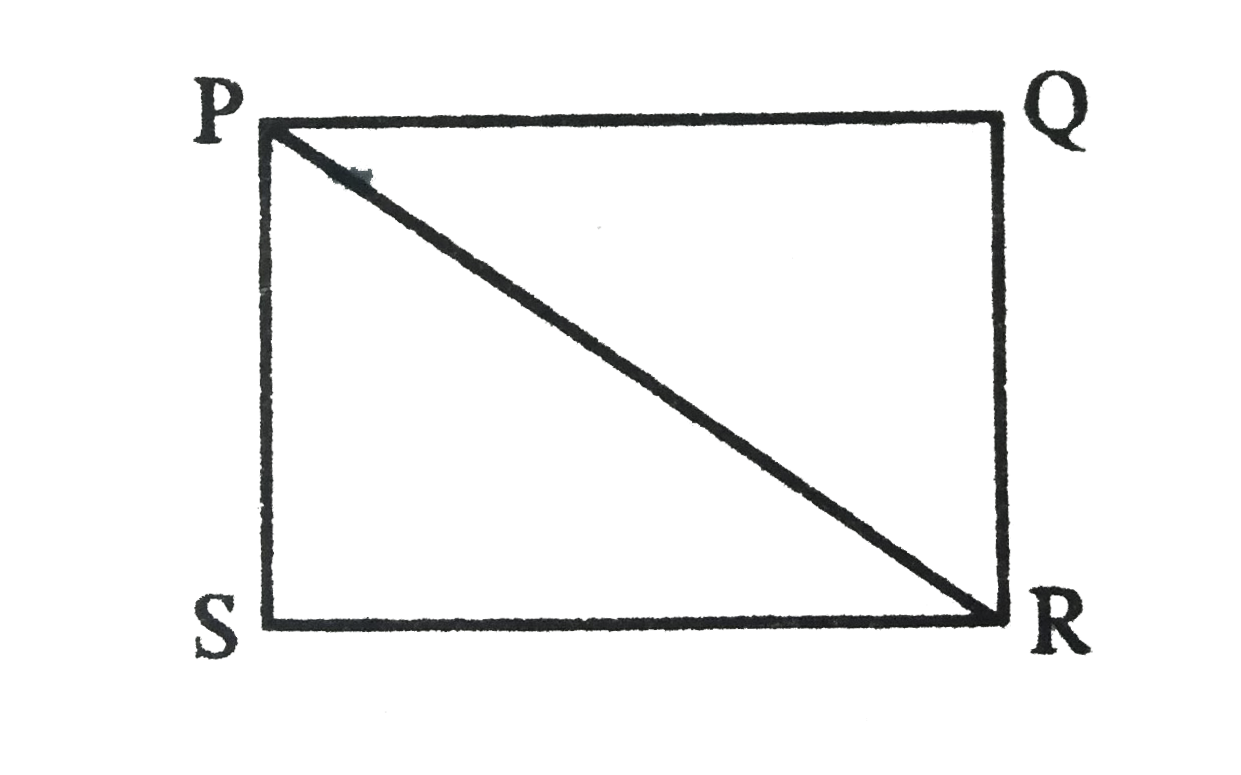 .
.
View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionThe moment of inertia of thin square plate ABCD of uniform thickness about an axis passing through the center O and perpendicular to the plane of the plate is
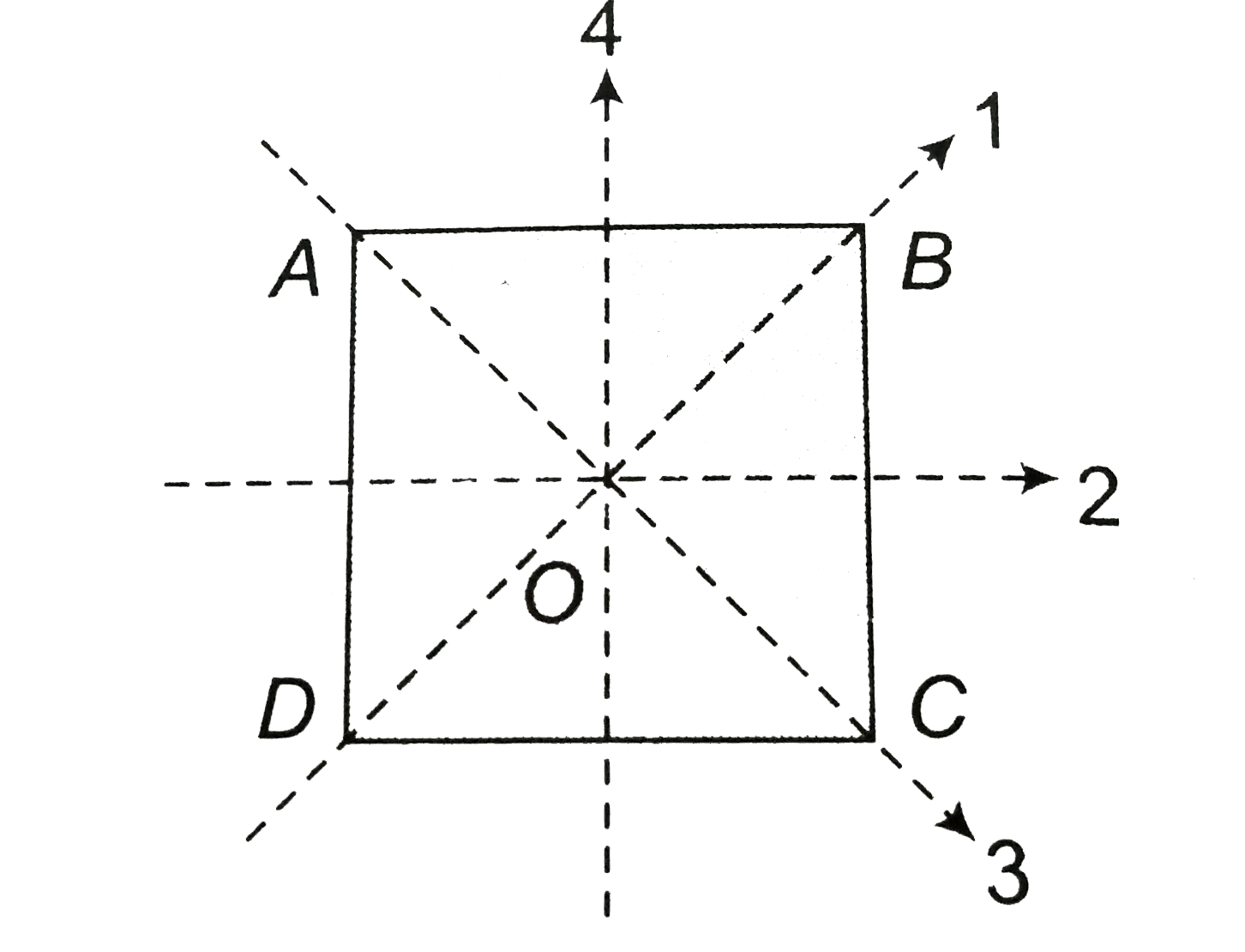
(i) I1+I2
(ii) I2+I4
(iii) I1+I3
(iv) I1+I2+I3+I4
where I1, I2, I3 and I4 are repectively moments of inertia about axes 1, 2, 3 and 4 which are in the plane of the plane
View Solution

