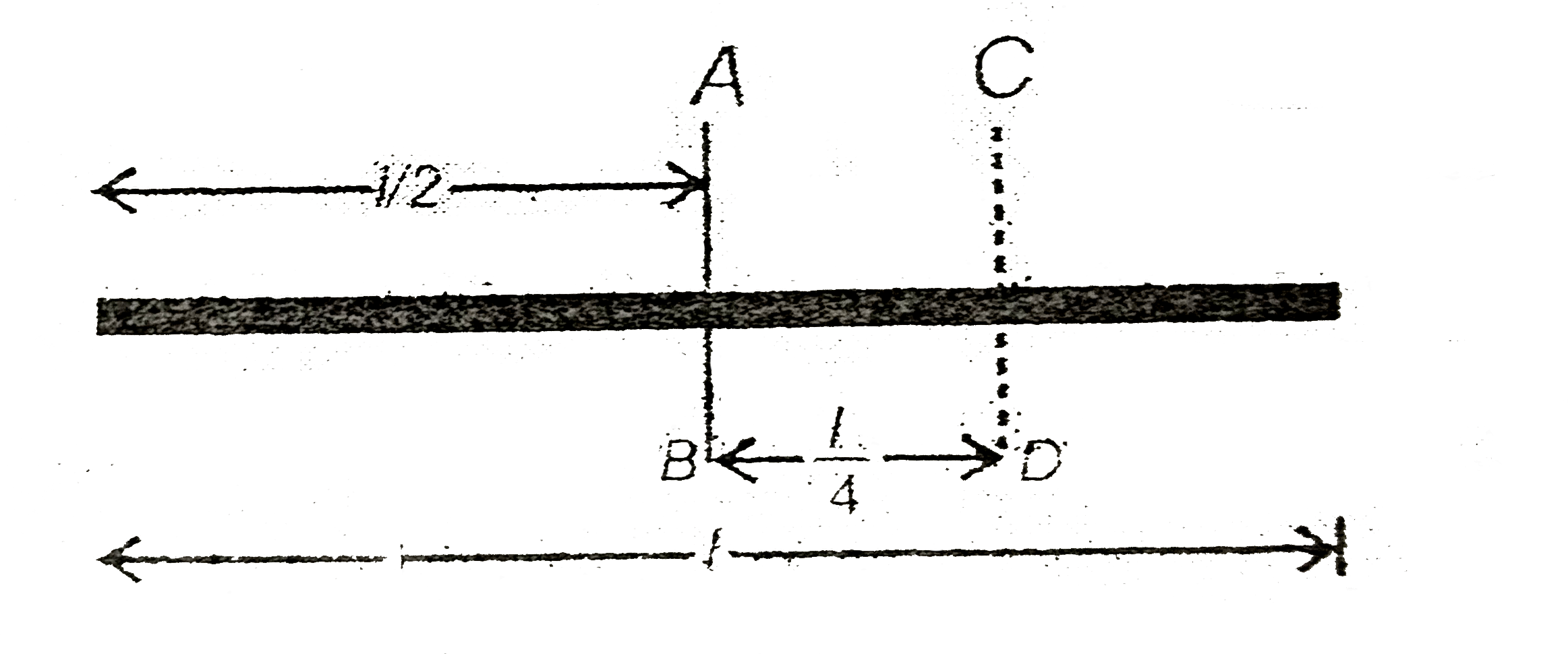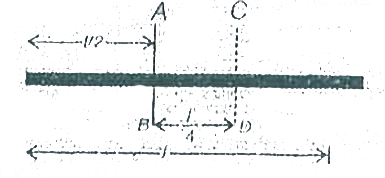Calculate the moment of inertia of each particle in Fig. about the indicated axis of rotation.

a. I=m(l2)2+m(l2)2=ml22
b. I=4ml2
c. I=ml2+m(l2)2=54ml2
d.I=2m(2l)2=8ml2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.3
Explore 15 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.4
Explore 11 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Exercise 2.1
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICSChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:INTEGER_TYPE
Explore 2 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Interger
Explore 2 Videos
Similar Questions
Knowledge Check
Two bodies have their moments of inertia l and 2l respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A2:1B1:2C√2:1D1:√2Two bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
A1:2B√2:1C2:1D1:√2Two bodies have their moments of inertia I and 2I, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
A2:1B1:2C√2:1D1:√2
Angular momentum of a particle is the moment of _______ of the particle about the axis rotation.
View SolutionThe angular momentum of a body is 31.4 Js and its rate of revolution is 10 cycles per second. Calculate the moment of inertia of the body about the axis of rotation.
View SolutionStatement-1 : Moment of inertia of a particle is same, whatever be the axis of rotation.
Statement-2 : Moment of inertia depends on mass and perpendicular distance of the particle from its axis of rotation.
View SolutionCalculate the moment of inertia of a body about its axis of rotation if its angular momentum is 62.8 Js and it has 10 revolutions per second.
View SolutionTwo bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
View Solution