A uniform ladder of 7m rests against a vertical wall with which it makes an angle of 45º the coefficient of friction between the ladder and the wall is 0.4 and that between ladder and the floor is 0.5. If a man whose weight is one half of that of the ladder ascends it how high will it be when the ladder slips?
X = Distance between A and the man when the ladder is at the point of slipping. W = Weight of the ladder Weight of man = W/2 = 0.5W Fr1 = 0.5R1 ...i Fr2 = 0.4R2 ...ii Resolving the forces vertically R1 + Fr2 – W – 0.5W = 0 R1 + 0.4R2 = 1.5W ...iii Resolving the forces Horizontally R2 – Fr1 = 0; R2 = 0.5R1 ...iv Solving equation iii and iv we get R2 = 0.625W Fr2 = 0.25W Now taking moment about point A W × 3.5cos45° + 0.5W × xcos45° – R2 × 7sin45° – Fr2 × 7cos45° Putting the value of R2 and Fr2 we get X = 5.25m.
Related Solutions
A uniform ladder is standing against a vertical smooth wall, resting on a horizontal floor. The ladder makes an angle of 45^(@) with the floor when its lower end is about to slip. What is the value of the coefficient of friction between the ladder and the floor?
View SolutionA uniform ladder of length rests against a smooth, vertical wall (figure). If the mass of the ladder is and the the coefficient of static friction between the ladder and the ground is and the minimum angle at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle with the horizontal floor. The coefficient of friction between the wall and the ladder is and that between the floor and the ladder is the normal reaction of the wall on the ladder is and that of the floor is if the ladder is about to slip. than
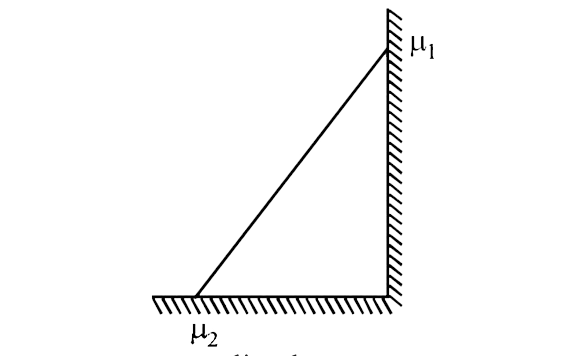
View SolutionIn the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle theta with the horizontal floor. The coefficient of friction between the wall and the ladder is mu_1 and that between the floor and the ladder is mu_2. the normal reaction of the wall on the ladder is N_1 and that of the floor is N_2. if the ladder is about to slip. than
View SolutionA ladder rests on the floor of a room, leaning agains a wall. If the coefficient of static friction between the ladder the floor is mu_(f) and that between ladder and is mu_(w) , what is the minimum angle theta that the ladder can make with the floor if the ladder is not to slip? Assume that the mass of the ladder is distributed uniformly.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA light ladder rests onn te rough floor of a room, leaning against a smooth wall. The ladder touches the wall at height above the floor. A man climbs up the ladder until the base of the ladder is on the verge of slipping. The coefficint of static friction between the foot of the ladder and floor is .
(a) What is the horizontal distance moved by the man?
(b) Solve part (a) if the ladder is uniform and has the same weight as the man and the base of the ladder is at a distance from the wall.
View SolutionThe length of a uniform ladder of mass m is 1. It leans against a smooth wall making an angle with the horizontal. What should be the force of friction between the floor and ladder so that the ladder does not slip ?
View SolutionA ladder on a horizontal floor leans against a vertical wall. The coefficients of friction of the floor and the wall with the ground are and respectively. If a man, whose weight is n times that of the ladder, wants to climb up the ladder, the minimum safe angle of the ladder with the floor is .
View SolutionA ladder of mass 30 kg and length 5 m is kept leaning against a vertical smooth wall. A man of mass 60 kg climbed up the length of the ladder. If the coefficient of friction between the floor and the ladder is 0.5, what should be the maximum distance of the foot of the ladder from the wall to avoid slipping?
View SolutionA uniform - ladder of length 70 m and weight W rests against a vertical wall at an angle of with the wall. The coefficient of friction of the ladder with the ground and the wall are and respectively. A man of weight W/2 climbs the ladder without slipping. The height in metres to which he can climb is
View SolutionA ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of with the ground . Find the height, upto which the ladder reaches.
View SolutionA ladder is placed along a wall such that its upper end is touching the top of the wall .The foot of the ladder is 10 ft away from the wall and the ladder is making an angle of with the ground . When a man starts climbing on it , it slips and now ladder makes an angle of with ground .How much did the ladder slip from the of the wall ?
View Solutionമതിലിന്മേൽ ഒരു ഏണി ചാരി വെച്ചിരിക്കുന്നു . ഏണിയുടെ ചുവട് മതിലിൽ നിന്ന് മീറ്റർ അകലെയാണ്. ഏണിയും തറയുമായുള്ള കോൺ യും . ഏണിയുടെ മുകളറ്റം തറയിൽ നിന്ന് എത്ര ഉയരത്തിലാണ് ?
View SolutionA uniform ladder of length L and mass M leans against a frictionless vertical wall. The ladder makes an angle theta with ground and the coefficient of the static friction between the ground and the foot of the ladder is mu . What maximum height a man of mass m can climb up the ladder so that the ladder will not skid?
View SolutionA ladder 6.5 m long is standing against a wall and the difference between the base of the ladder and wall is 5.2 m. If the top of the ladder now slips by 1.4 m, then by how much will the foot of the ladder slip?
View SolutionA ladder 6.5 m long is standing against a wall and the difference between the base of the ladder and wall is 5.2 m. If the top of the ladder now slips by 1.4 m, then by how much will the foot of the ladder slip?
View SolutionA ladder is resting with a vertical wall at an angle of . If a man is ascending the ladder of at the rate of 6 feet/sec, then the rate at which the man is approaching the wall, is
View SolutionA ladder, 10 metre long rests with one end against a smooth vertical wall and the other end on the ground which is rough, the coefficient of friction being . The foot of the ladder being 2 metre from the wall. A amn whose weight is 4 times that of the ladder can ascend before it be givens to slip is
View Solution