An RLC circuit has a sinusoidal source of emf. The average rate at which the source supplies energy is 5 nW. This must also be: A. the average rate at which energy is stored in the capacitor B. the average rate at which energy is stored in the inductor C. the average rate at which energy is dissipated in the resistor D. twice the average rate at which energy is stored in the capacitor E. three times the average rate at which energy is stored in the inductor
C. the average rate at which energy is dissipated in the resistor
Related Solutions
In steady state, calculate energy stored in capacitors shown in Fig. and the rate at which battery supplies energy
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionConsider the situation of the previous problem. Find the average electric field energy stored in the capacitor and the average magnetic field energy stored in the coil.
View SolutionConsider the situation of the previous problem. Find the average electric field energy stored in the capacitor and the average magnetic field energy stored in the coil.
View SolutionThe circuit shown in fig. Is in steady state.

i. Find the energy stored in the capacitors shown in fig.
ii. Find the rate at which battery supplies energy.
View SolutionThe circuit shown in fig. Is in steady state. i. Find the energy stored in the capacitors shown in fig. ii. Find the rate at which battery supplies energy.
View SolutionA coil of reistance 5Omega and inductance 1H is connected to a battery of 10V. At t = 0s , calculate (i) the current in the circuit (ii) the rate of rise of current (iii) the rate at which energy is supplied by the battery, (iv) the rate at which energy is dissipated as heat and (v) the rate at which energy is stored in the magnetic field of the coil.
View SolutionA capacitor of capacitance C is connected to a battery of emf E at t = 0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionA Henry inductor coil is connected to a resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
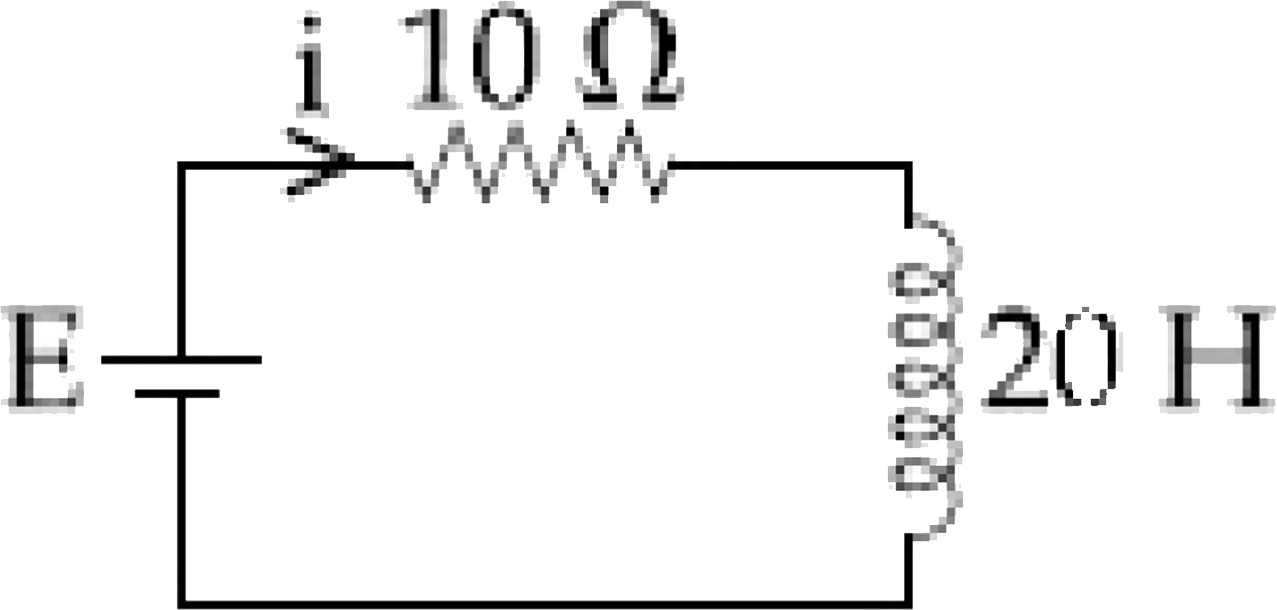
View SolutionAn inductor of self-inductance L and resistor of resistance R are connected in series to a battery of emf E and negligible resistance.Calculate the maximum rate at which energy is stored in the inductor.
View SolutionAn L-C-R series circuit with L = 0.120 H, R = 240 a , and C = 7.30muF carries an rms current of 0.450 A with a frequency of 400 Hz . (a) What are the phase angle and power factor for this circuit? (b) What is the impedance of the circuit? (c) What is the rms voltage of the source? (d) What average power is delivered by the source? (e) What is the average rate at which electrical energy is converted to thermal energy in the resistor? (f) What is the average rate at which electrical energy is dissipated ( converted to other forms) in the capacitor? (g) In the inductor ?
View SolutionAn L-C-R series circuit with L = 0.120 H, R = 240 a , and C = 7.30muF carries an rms current of 0.450 A with a frequency of 400 Hz . (a) What are the phase angle and power factor for this circuit? (b) What is the impedance of the circuit? (c) What is the rms voltage of the source? (d) What average power is delivered by the source? (e) What is the average rate at which electrical energy is converted to thermal energy in the resistor? (f) What is the average rate at which electrical energy is dissipated ( converted to other forms) in the capacitor? (g) In the inductor ?
View SolutionIf a battery of emf E, internal resistance r is being charged by a current I from a charge then the rate at which energy is supplied by charger is ……. And the rate at which chemical energy is stored in the battery is ……
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View Solution