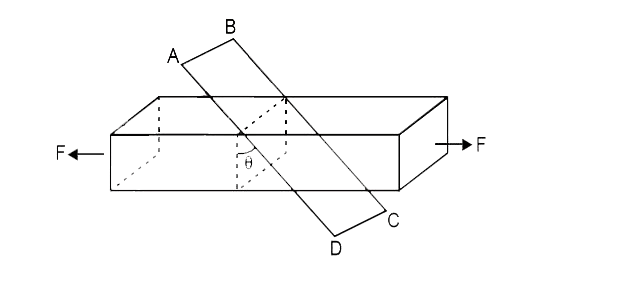
A bar is subjected to equal and opposite forces as shown in the figure. PQRS is a plane making angle θ with the cross-section of the bar. If the area of cross-section be ‘A’ then what is the tensile stress on PQRSa F/Ab Fcosθ/Ac Fcos2θ/ A d F/A cosθ
Correct option c Fcos2θ/ A Explanation:
Related Solutions
A bar is subjected to equal and opposite forces as shown in the figure. PQRS is a plane making angle with the cross-section of the bar. If the area of cross-section be 'A', then what is the tensile stress on PQRS

View SolutionThe bar is subjected to equal and opposite forces as shown in the figure PQ is plane making angle with the cross-section of the bar. If the area of cross-section be 'a', then what is the tensile stress on PQ ?
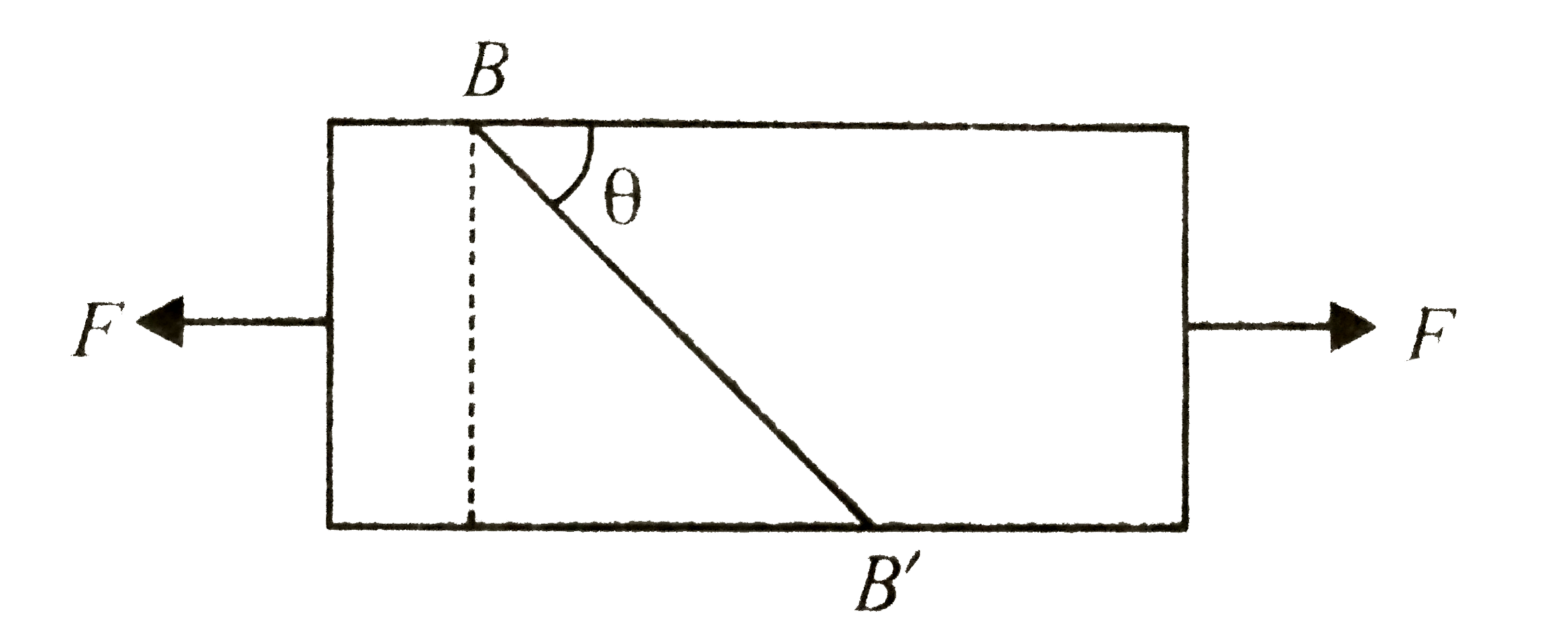
View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length. The ratio of tensile stress to the shearing stress on the plane BB' is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.
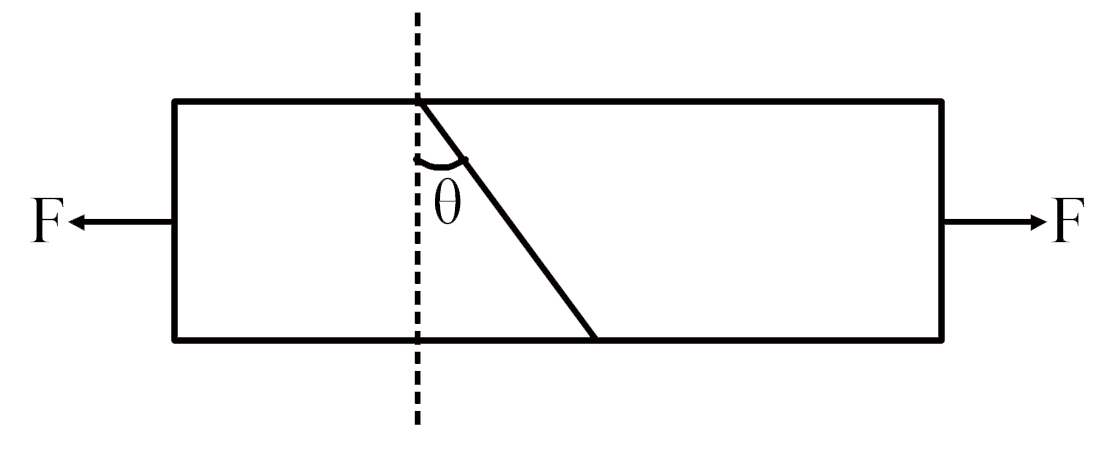
The tensile stress at this plane in terms of F, A and is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.

The tensile stress at this plane in terms of F, A and is
View SolutionEqual and opposite forces are applied on a rod as shown in the figure. From any cross-section of the plane PQRS rod theta makes an angle. If the area of cross section of the rod is 'A', then the tensile stress on PQRS will be
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.
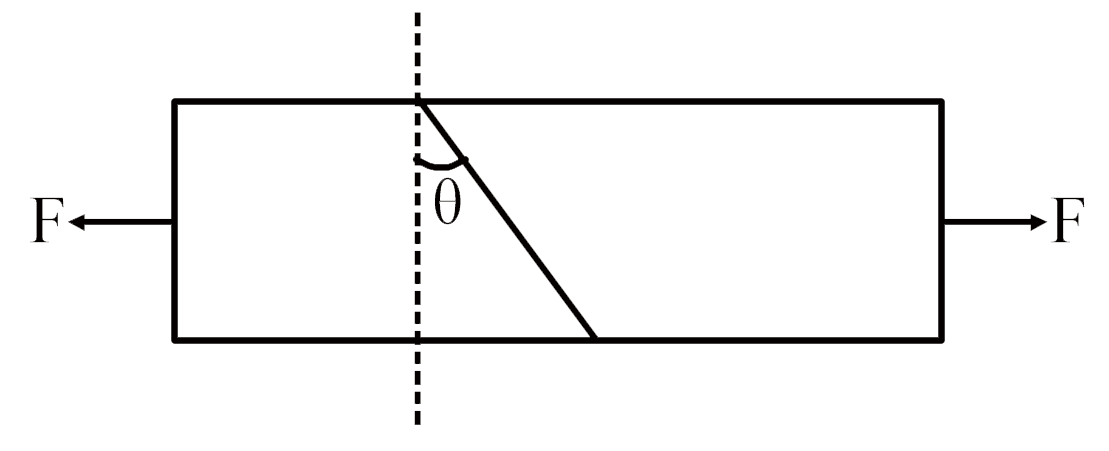
In the above problem, for what value of is the tensile stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle theta with a plane at right angles to the bar as shown in figure. The shearing stress at the plane, in terms of F, A and theta is
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar.
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar. (a) What is the tensile stress at this plane in terms of F, A and @ ? (b) What is the shearing stress at the plane, in terms of F, A and (c) For what value of is the tensile stress a maximum? (d) For what value of is the shearing stress a maximum?

View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length

View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle as shown, find
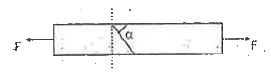
the shearing stress at this plane
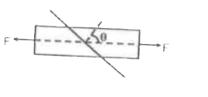
View SolutionFig shows a bar of uniform cross section of area s . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F . ABCD is a plane trough the bar and inclined at angle theta with the perpendicular to the length of the bar. Normal stress at the plane which is inclined with the plane perpendicular to the length of the bar is -
View SolutionTwo force are equal and opposite in direction exerted on a bar (rod) as shown in figure. Hence plane PQ makes an angle with the cross-section 'a'. Find the tensile stress on PQ.

View SolutionFig shows a bar of uniform cross section of area s . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F . ABCD is a plane trough the bar and inclined at angle theta with the perpendicular to the length of the bar. Shear stress on theplane which is inclined with the plane perpendicular to the length of the bar is
View SolutionFig. shows a bar of uniform rectangular cross-section of area S. Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F. ABCD is a plane through the bar and inclined at angle phi with the plane perpendicular to the length of the bar. Shear stress on the said plane will be maximum for phi = :
View SolutionFig shows a bar of uniform cross section of area . Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude . ABCD is a plane trough the bar and inclined at angle with the perpendicular to the length of the bar.
Shear stress on the inclined plane will be maximum for
View SolutionA bar of cross section is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of is the tensile stress maximum?
d. For what value of is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle with the axis of the bar.
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of is the tensile stress is maximum ?
(d) for what value of is the shearing stress maximum ?
View SolutionA bar of cross section is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of is the tensile stress maximum?
d. For what value of is the shearing stress maximum?
View Solution