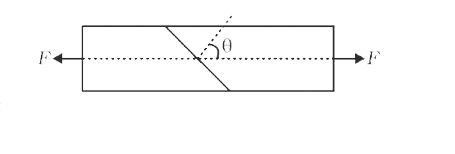
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
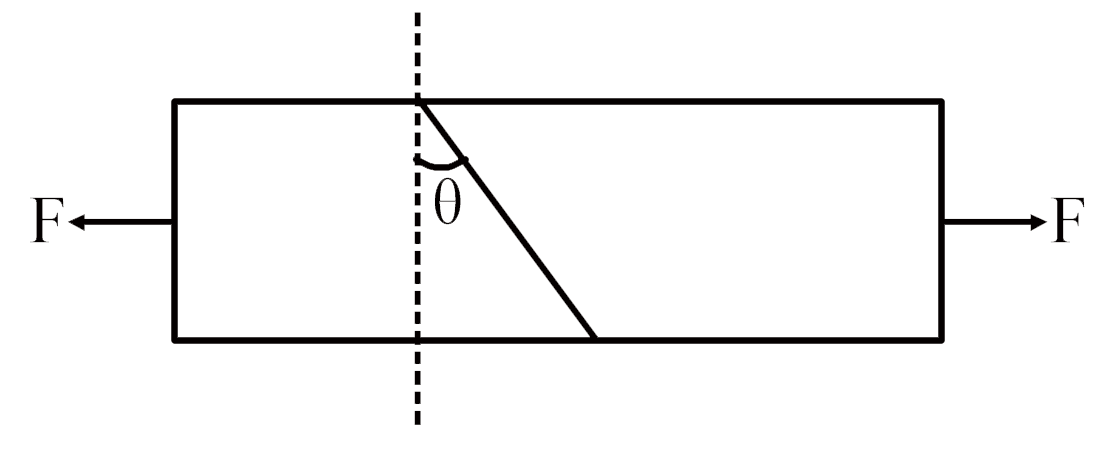
The tensile stress at this plane in terms of F, A and θ is
What is the tensile stress at this plane in terms of F,A and θ ?
What is the sherating stress at the plane, in terms of F,A and θ ?
For what value of θ is the tensile stress a maximum ?
For what valule of θ is shearing stress a maximum?
The correct Answer is:A, B, C, D
(a) tensile stress =FcosθA/cosθ=Fcos2θA
(b) shearing stress =FsinθA/cosθ=FAsinθcosθ
for max. tensile stress
θ=0∘
(d) for max. shering stress
θ=45∘
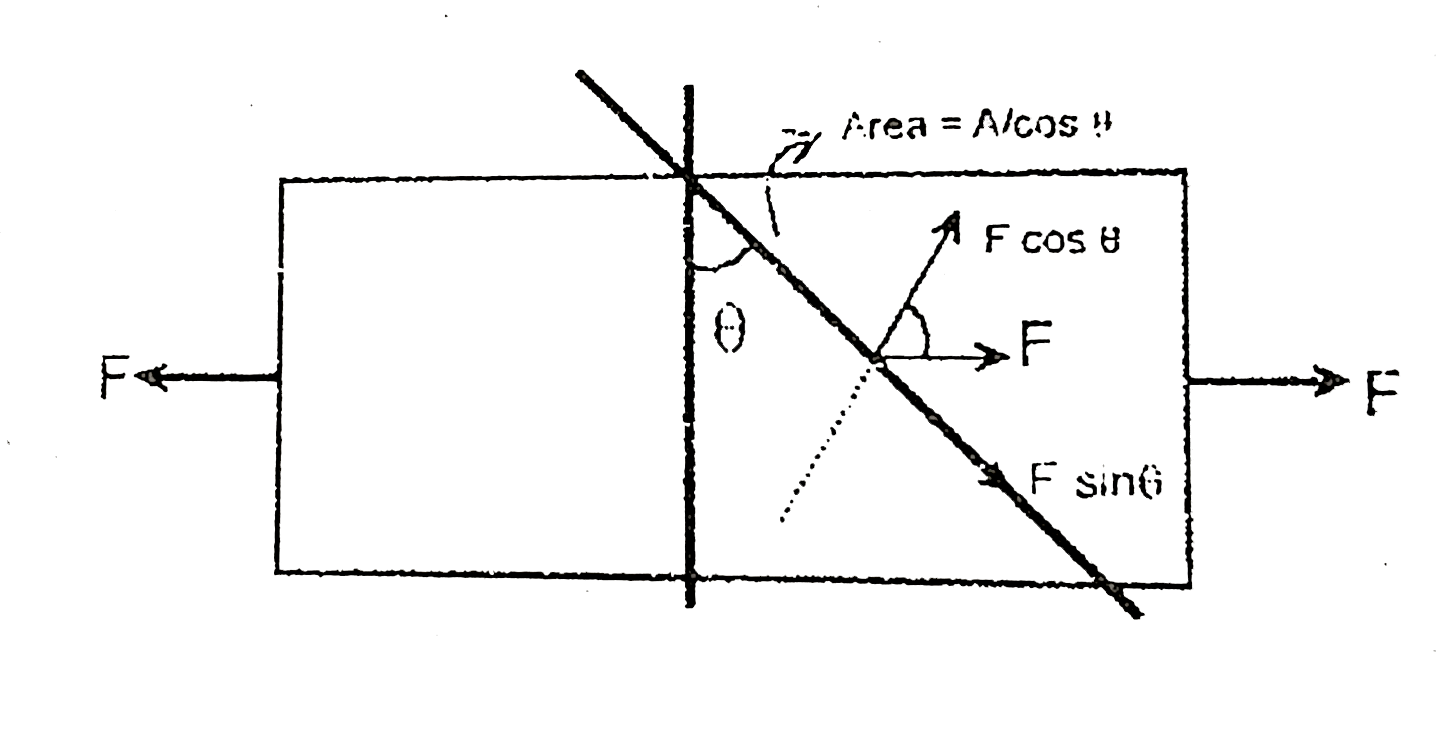
Topper's Solved these Questions
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 1 PART - II
14 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Exercise- 2 PART - I
9 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration
2 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise
43 Videos
Similar Questions
A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View Solution
Knowledge Check
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
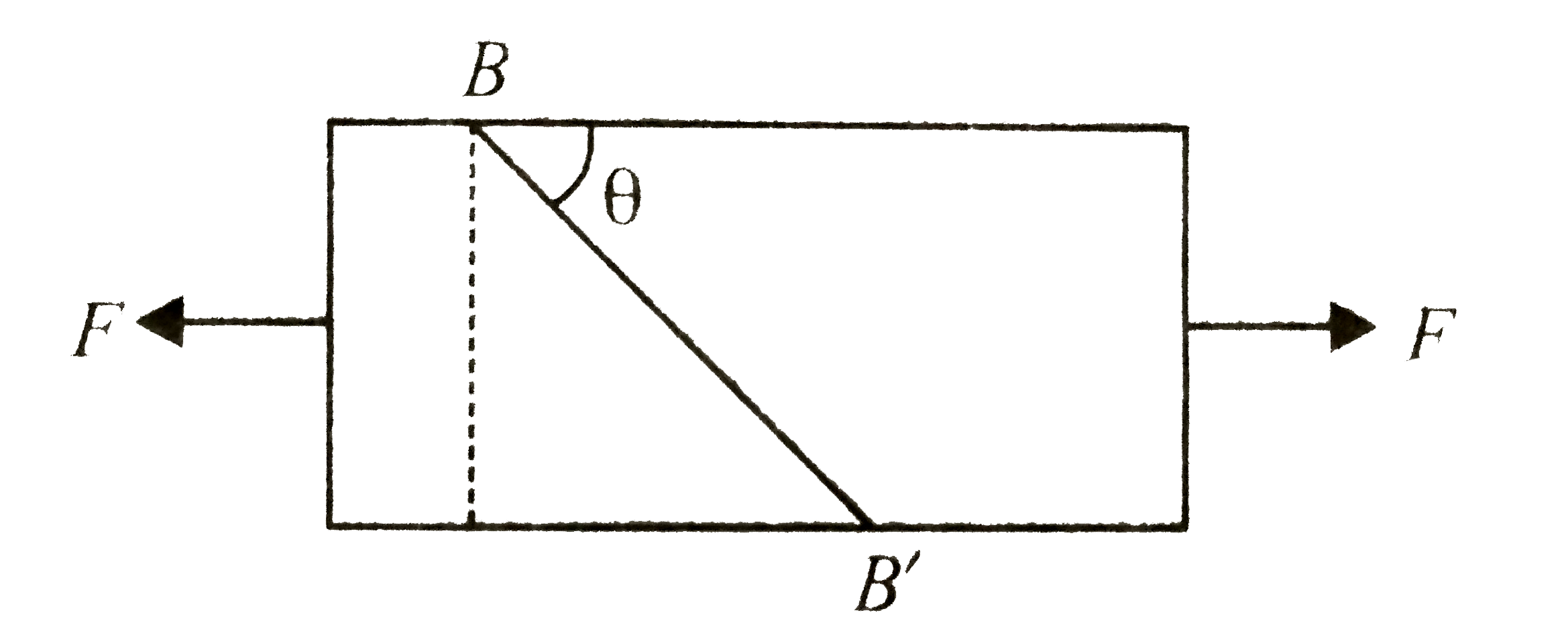 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθ
A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
View SolutionA rod area of cross section A is being acted upon by two forces F - F as shown in figure. Consider a section ab of rod whose normal makes angle θ with horimontal. The shear stress upon this section is maximum when θ=180∘n. Find n.

View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionA massless uniform rod is subjected to froce F at its free end as shown in figure. The ratio of tensile stress at plane P1 to stress at P2 is
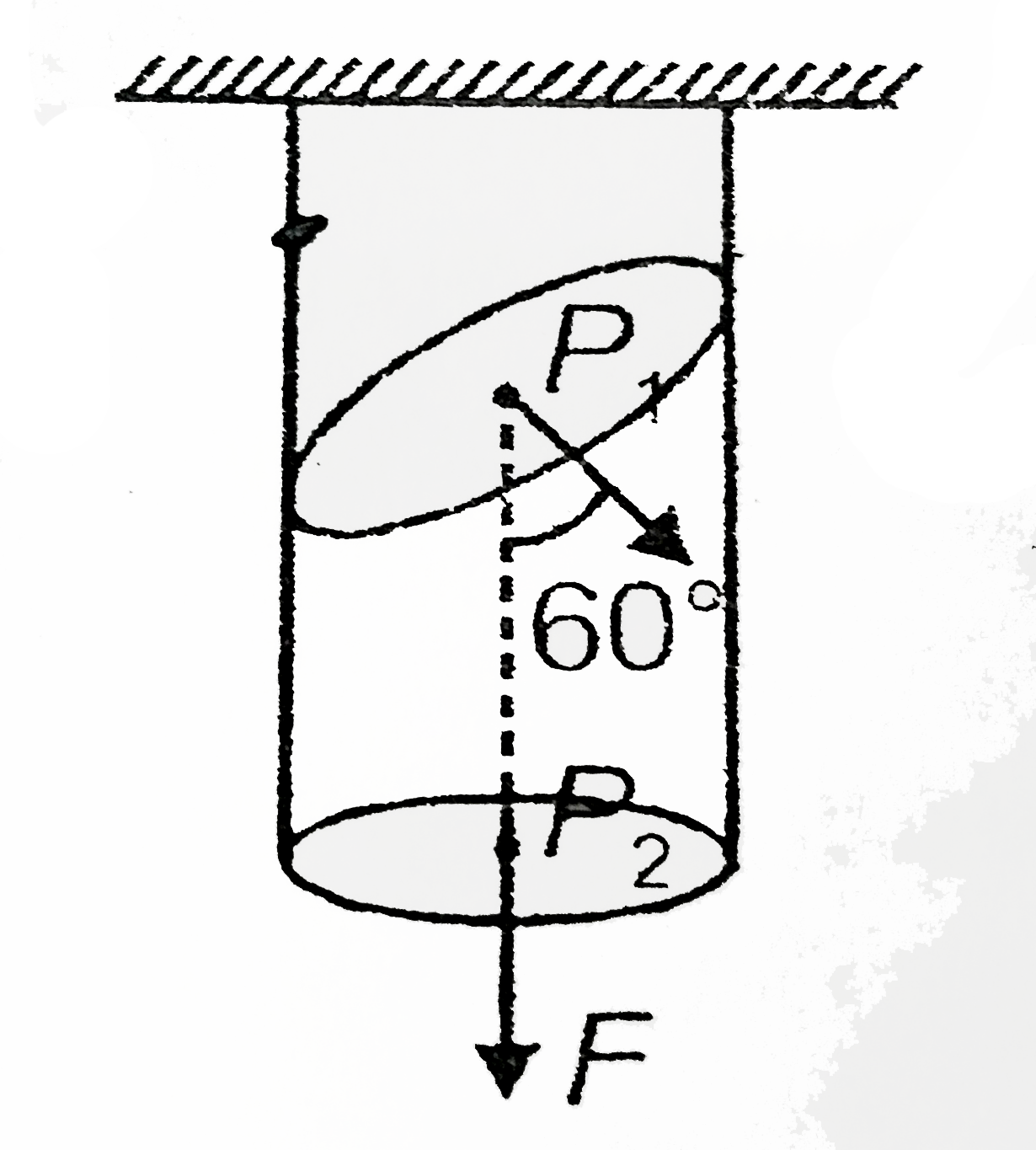
View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is

View SolutionA ball is projected form a point A on a smooth inclined plane which makes an angle a to the horizontal. The velocity of projection makes an angle θ with the plane upwards. If on the second bounce the ball is moving perpendicular to the plane, find e in terms of α and θ. Here e is the coefficient of restitution between the ball and the plane.
View SolutionA horizontal force F is applied to a block of mass m on a smooth fixed inclined plane of inclination θ to the horizontal as shown in the figure. Resultant force on the block up the plane is:

View Solution
