A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
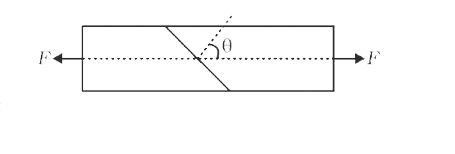
(i) The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on the plane.
∴ Area of plane section =Asecθ
Tensile stress =ForceArea=FcosθAsecθ =FAcos2θ
(ii) Shearing stress applied on the plane
So , F=Fsinθ
Shearing stress =ForceArea=FsinθAsecθ=FAsinθcosθ
=F2Asin2θ [∵sin2θ=2sinθcosθ]
(iii) Tensile stress will be maximum when cos2θ is maximum i.e., cosθ=1orθ=0∘ (iv) Shearing stress will be maximum when sin2θ is maximum i.e . sin2θ=1 or 2θ=90∘orθ=45∘ .
Topper's Solved these Questions
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -1
Explore 90 Videos
- PROPERTIES OF MATTERBook:VMC MODULES ENGLISHChapter:PROPERTIES OF MATTERExercise:Level -2
Explore 50 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
- QUIZBook:VMC MODULES ENGLISHChapter:QUIZExercise:PHYSICS
Explore 30 Videos
Similar Questions
A bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View Solution
Knowledge Check
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
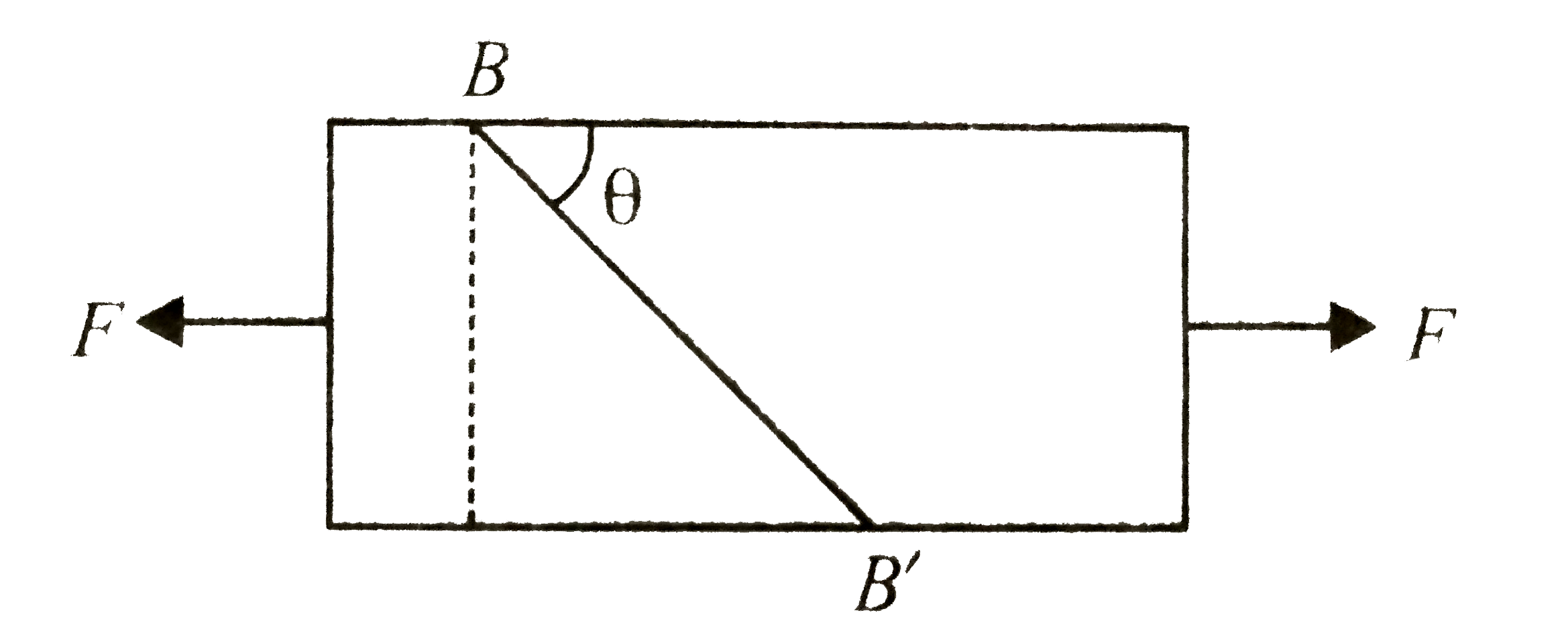 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθIn the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘
What is the length of ¯¯¯¯¯¯QR ?A5B5√22C10√2D5√2
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
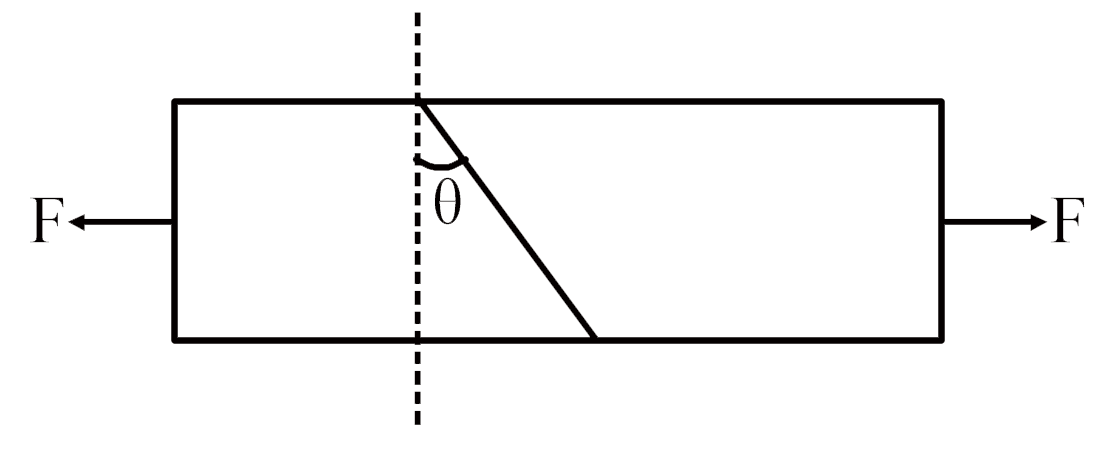
The tensile stress at this plane in terms of F, A and θ is
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionTensile stress is possible in
View SolutionA rod area of cross section A is being acted upon by two forces F - F as shown in figure. Consider a section ab of rod whose normal makes angle θ with horimontal. The shear stress upon this section is maximum when θ=180∘n. Find n.

View SolutionThe ratio of tensile stress to the longitudinal strain is defined as
View Solution
