The ratio of tensile stress to the longitudinal strain is defined as
Bulk modulus
Young's modulus
Shear modulus
Compressibility
The correct Answer is:B
To solve the question regarding the ratio of tensile stress to longitudinal strain, we can follow these steps:
1. Define Tensile Stress:
- Tensile stress (σ) is defined as the force (F) applied per unit area (A) over which the force is distributed.
- Mathematically, it is expressed as:
σ=FA
2. Define Longitudinal Strain:
- Longitudinal strain (ε), also known as tensile strain, is defined as the change in length (ΔL) divided by the original length (L) of the material.
- Mathematically, it is expressed as:
ϵ=ΔLL
3. Formulate the Ratio:
- The ratio of tensile stress to longitudinal strain is given by:
σϵ
4. Substitute the Definitions:
- Substitute the expressions for tensile stress and longitudinal strain into the ratio:
σϵ=FAΔLL
5. Simplify the Expression:
- To simplify, we can multiply by the reciprocal of the strain:
σϵ=FA⋅LΔL=F⋅LA⋅ΔL
6. Identify the Result:
- This ratio is defined as Young's modulus (E), which is a measure of the stiffness of a solid material.
- Therefore, we conclude:
σϵ=E
Final Answer:
The ratio of tensile stress to longitudinal strain is defined as Young's modulus.
---
- Tensile stress (σ) is defined as the force (F) applied per unit area (A) over which the force is distributed.
- Mathematically, it is expressed as:
σ=FA
- Longitudinal strain (ε), also known as tensile strain, is defined as the change in length (ΔL) divided by the original length (L) of the material.
- Mathematically, it is expressed as:
ϵ=ΔLL
- The ratio of tensile stress to longitudinal strain is given by:
σϵ
- Substitute the expressions for tensile stress and longitudinal strain into the ratio:
σϵ=FAΔLL
- To simplify, we can multiply by the reciprocal of the strain:
σϵ=FA⋅LΔL=F⋅LA⋅ΔL
- This ratio is defined as Young's modulus (E), which is a measure of the stiffness of a solid material.
- Therefore, we conclude:
σϵ=E
The ratio of tensile stress to longitudinal strain is defined as Young's modulus.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:HOTS
Explore 8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:STRESS-STRAIN CURVE
Explore 5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT FINGERTPS ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:NCERT Exemplar
Explore 5 Videos
- MOTION IN A PLANE Book:NCERT FINGERTPS ENGLISHChapter:MOTION IN A PLANE Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
Knowledge Check
The ratio of shearing stress to the shearing strain is defined as
AYoung's modulusBbulk modulusCshear modulusDcompressibilityA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length. The ratio of tensile stress to the shearing stress on the plane BB' is
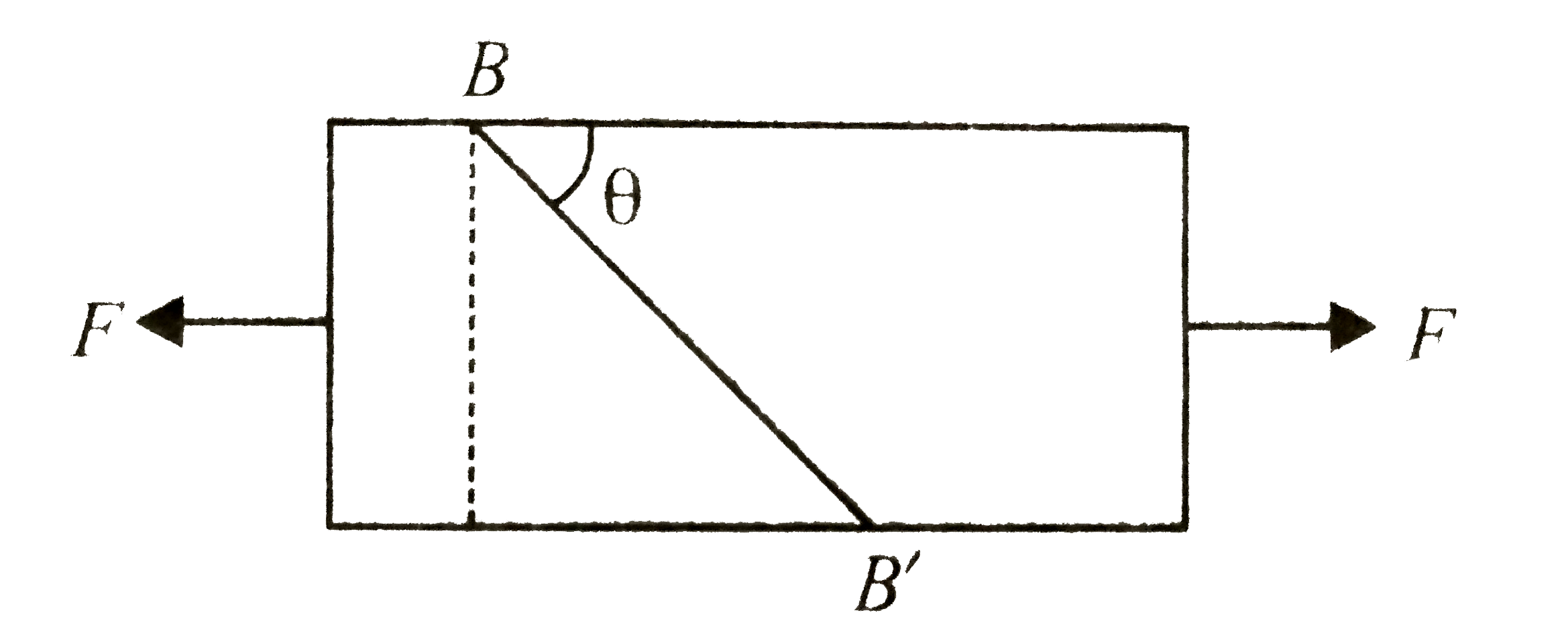 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθ
In figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinal strains developed in the two wires.

View Solution(i) State Hook's law.
(ii) Draw a labelled graph of tensile stress against tensile strain for a metal wire upto the breaking point. Shhow on your graph the region in which Hooke's law is obeyed.
What is the significance of the area between the graph and the strain axis withing the Hooke's law region?
View SolutionThe elastic energy per unit volume is terms of longitudinal strain σ and Young's modulus Y is
View SolutionThe young's modulus for steel is much more then that for rubber. For the same longitudinal strain, which one will have greater tensil stress ?
View SolutionTensile stress is possible in
View SolutionThe Poisson’s ratio for a metal is 0.25. If lateral strain is 0.0125, the longitudinal strain will be
View Solution

