The system in Fig. consists of a homogeneous pulley mass M radius r a block mass m and a spring spring constant k. Determine the equation of motion for the block and its solution for the initial conditions x0 = 0 v0 = v0. Neglect the mass of the string and any lateral motion.
We separate the pulley and the block and measure the displacements x of the block and xA of point A from the position of equilibrium. With this choice we do not have to consider the weights Mg and mg in the freebody diagram. Thus the equations of motion are If we use the kinematic relations Π=: b instantaneous center of rotation see the figure and ΘA = Mr2/2 we can solve the equations of motion for x and obtainThe general solution of this differential equation is given byxt = A cos ωt + B sin ωt . The initial conditionslead to
Related Solutions
Figure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m . The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find: a. the maximum elongation in the spring. b. the maximum speed of the block m . Neglect the mass of the spring and that of the string. Also neglect the friction.
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m . The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find: a. the maximum elongation in the spring. b. the maximum speed of the block m . Neglect the mass of the spring and that of the string. Also neglect the friction.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstreatched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View Solutionद्रव्यमान के एक ब्लॉक को द्रव्यमान M के दूसरे ब्लॉक में स्प्रिंग नियतांक की स्प्रिंग ( द्रव्यमान नगण्य ) द्वारा जोड़ दिया जाता है । ब्लॉक एक चिकने समतल पर रखे हुए हैं । प्रारंभ में ब्लॉक स्थिर है तथा स्प्रिंग सामान्य स्थिति में है, तब द्रव्यमान M के ब्लॉक को एक नियत बल f द्वारा खींचा जाता है । द्रव्यमान m के ब्लॉक पर आरोपित बल होगा -
View Solutionm द्रव्यमान का एक ब्लॉक, M द्रव्यमान के दूसरे ब्लॉक से एक द्रव्यमान रहित तथा स्प्रिंग नियतांक K की स्प्रिंग से बँधा है | ब्लॉक चिकने क्षैतिज तल पर रखे हैं | प्रारम्भ में ब्लॉक विरामावस्था में है तथा स्प्रिंग बिना खिंची है | अब यदि M द्रव्यमान के ब्लॉक को एक नियत बल f लगाकर खींचा जाता है तो m द्रव्यमान के ब्लॉक पर लगा बल होगा :
View SolutionA block of mass m is connected to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially, the blocks are at rest and the spring is unstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is upstretched when a constant force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solutionएक m द्रव्यमान का गुटका स्प्रिंग नियतांक k की स्प्रिंग से ऊर्ध्वाधर रूप से लटक रहा है। यदि द्रव्यमान को ऊर्ध्वाधर रूप से दोलन कराया जाता है, तो इसकी कुल ऊर्जा होती है
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
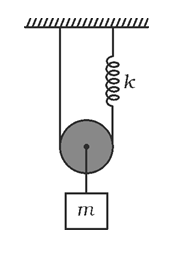
View SolutionFind the time period of oscillation of block of mass m. Spring, and pulley are ideal. Spring constant is k.
View Solution