Point A of the rod in Fig. moves with constant velocity vA to the left. Determine the velocity and the acceleration of point B of the rod point of contact with the step as a function of the angle ϕ. Find the path yx of the instantaneous center of rotation.
We use the coordinate system with the basis vectors er and eϕ as shown in the fiure .than the velocity of point A is given byThe velocity vB of point B points in the direction of the direction of the rod does not lift off the step. thus In order to determine the acceleration of point B we use the relationaB = aA + arAB + aϕAB whereaA = 0 arAB = −aϕ2er aϕAB = aϕ¨eϕ.The angular acceleration of the rod is found by differentiating its angular velocity ˙ϕ:
Related Solutions
The velocity of point A on the rod is (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
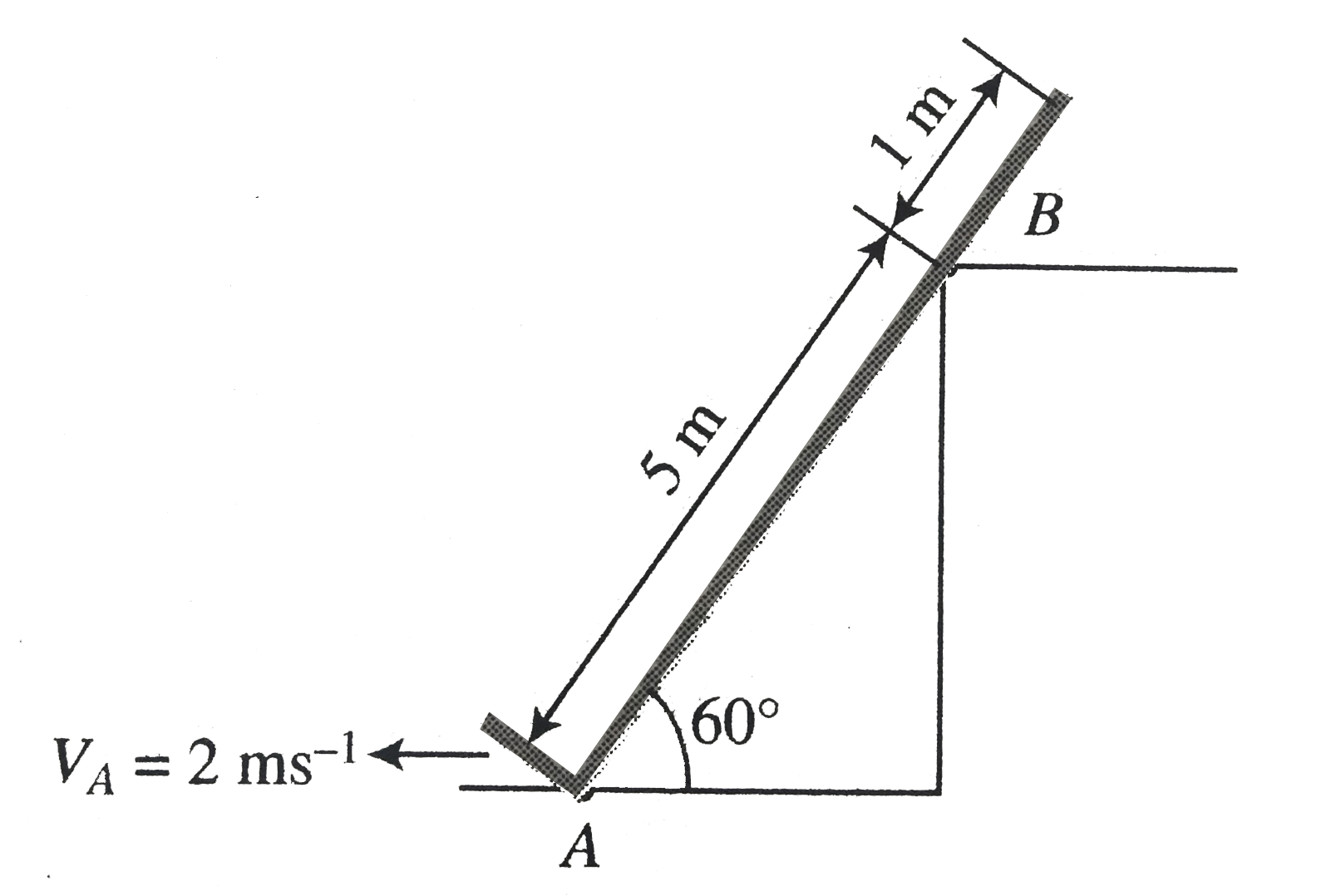
View SolutionThe velocity of point A on the rod is 2ms^(-1) (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
View SolutionA rod of length l is moving in a vertical plane ( x-y ) when the lowest point A of the rod is moved with a velocity v . find the a angular velocity of the rod and b velocity of the end B .
View Solutionएक छड़ के दो बिन्दु, छड़ के लम्बवत समान दिशा में 3v तथा v वेग से गति करते हैं। दोनो बिन्दु एक दूसरे से .r. दूरी पर हैं तो छड़ का कोणीय वेग होगा :
View SolutionIf the ends of rod of length L have velocities and , find the velocity of mid point of the rod.
View SolutionIf the ends of rod of length L have velocities barV_(A) and barV_(B) , find the velocity of mid point of the rod.
View SolutionThe rod of length rotates with an angular velocity an the point moves with velocity and acceleration . Find the velocity and acceleration of .
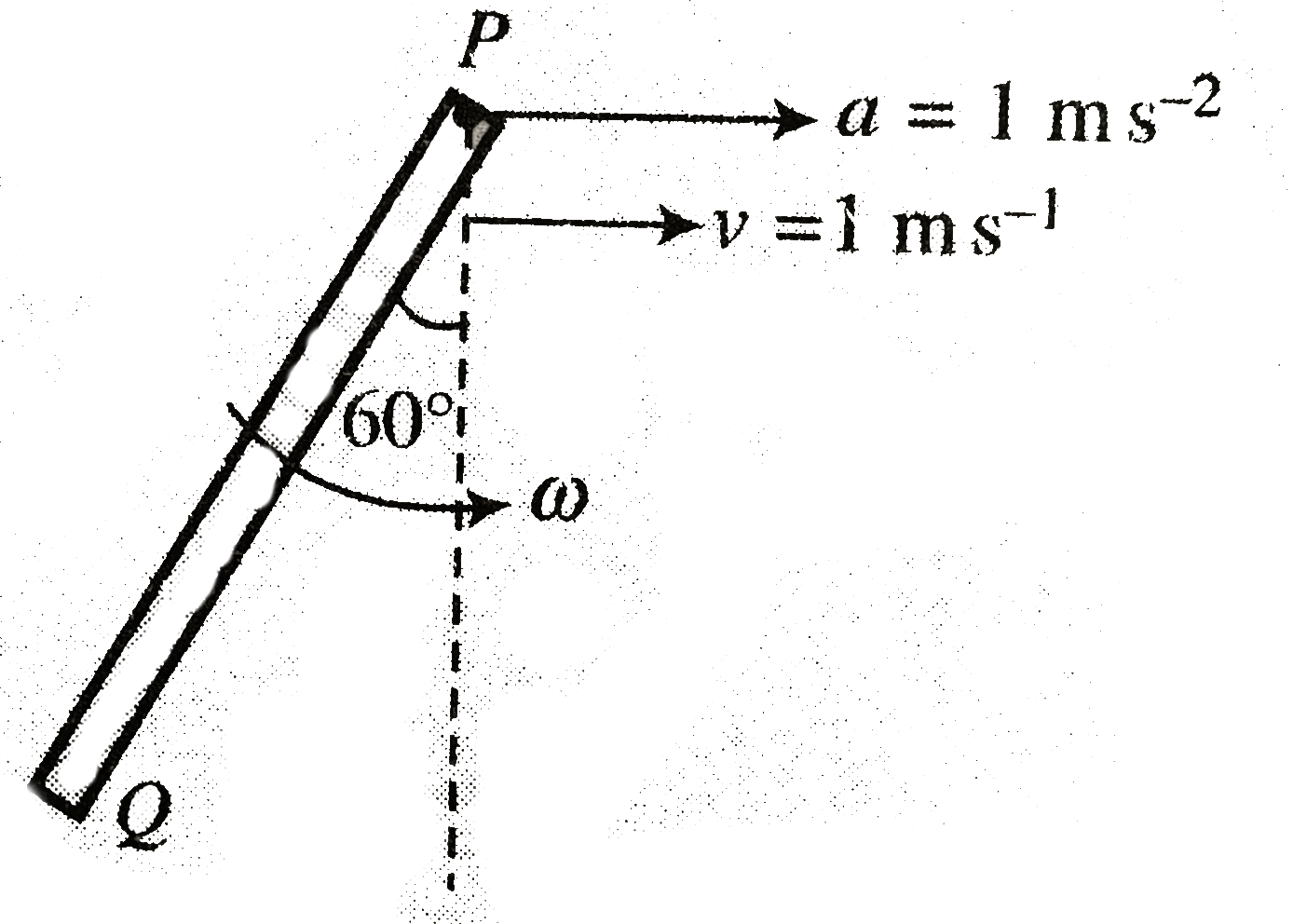
View SolutionThe rod of length rotates with an angular velocity an the point moves with velocity and acceleration . Find the velocity and acceleration of .
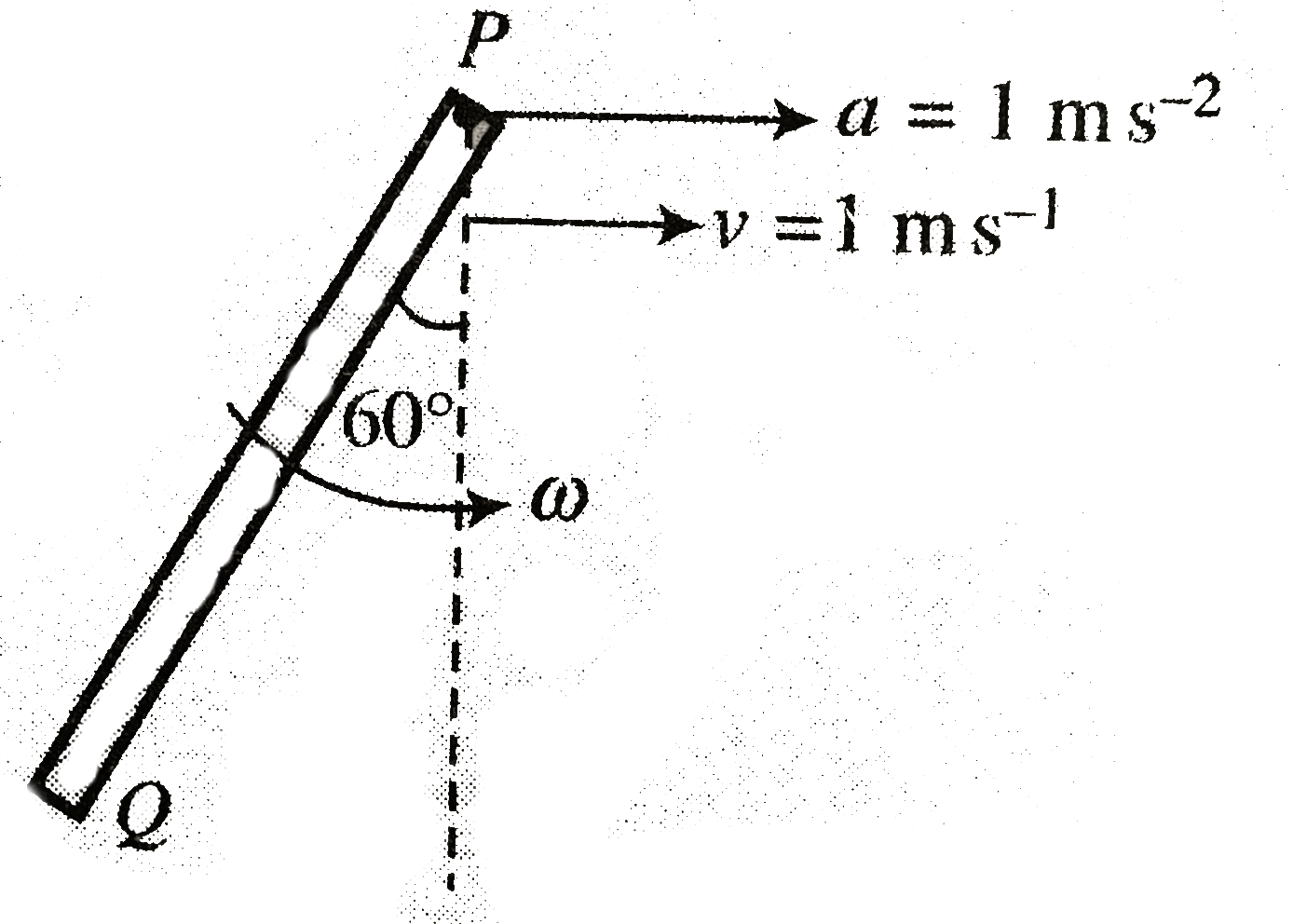
View SolutionA rod od length is moving in a vertical plane () when the owest point of the rod is moved with a velociy . find the a angular velocity of the rod and velocity of the end .

View SolutionAs shown in the figure, a rod moves with v = 2 m/sec & rotates with omega = 2pi rad/sec. Find the point on the rod whose velocity is zero in this frame.
View SolutionAs shown in the figure, a rod moves with v = 2 m/sec & rotates with omega = 2pi rad/sec. Find the point on the rod whose velocity is zero in this frame.
View SolutionFor particle moving on circular path with constant speed angle between instantaneous velocity and instantaneous acceleration will be …... .
View Solutionਇੱਕ 12 ਸੈ.ਮੀ. ਲੰਬੀ ਛੜ ਇਸ ਪ੍ਰਕਾਰ ਚਲਦੀ ਹੈ ਕਿ ਇਸਦੇ ਸਿਰੇ ਨਿਰਦੇਸ਼ ਅੰਕ ਧੁਰਾਂ ਨੂੰ ਸਪਰਸ਼ ਕਰਦੇ ਹਨ।ਛੜ ਦੇ ਬਿੰਦੂ P ਦਾ ਬਿੰਦੂ ਪਥ ਪਤਾ ਕਰੋ ਜੋ x-ਧੁਰੇ ਦੇ ਸੰਪਰਕ ਵਾਲੇ ਸਿਰੇ ਤੋਂ 3 ਸੈ.ਮੀ. ਦੂਰ ਹੈ।
View SolutionA rigid rod of length 1 is rested against a vertical wall (x-axis) as shown in the figure. The other end of the rod is on the horizontal floor. Point A is pushed down with a constant velocity. The path to the center of the rod is:
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity omega as shown in the figure. The rod maintains a constant angle theta with the vertical. What angle will the rod make with the vertical
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity omega as shown in the figure. The rod maintains a constant angle theta with the vertical. What angle will the rod make with the vertical
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle .
View SolutionA particle is moving with a constant speed in a circular path. Find the ratio of average velocity to its instantaneous velocity when the particle rotates an angle theta =((pi)/(2)) .
View SolutionA projectile is at the highest point of its journey. The angle between the instantaneous velocity and acceleration is
View SolutionA rod 'A' constrained to move in vertical direction rests on a wedge B, as shown in the Fig. Find the accelerations of rod A and wedge B instantaneously after system is released from rest, neglecting friction at all the contact surfaces.
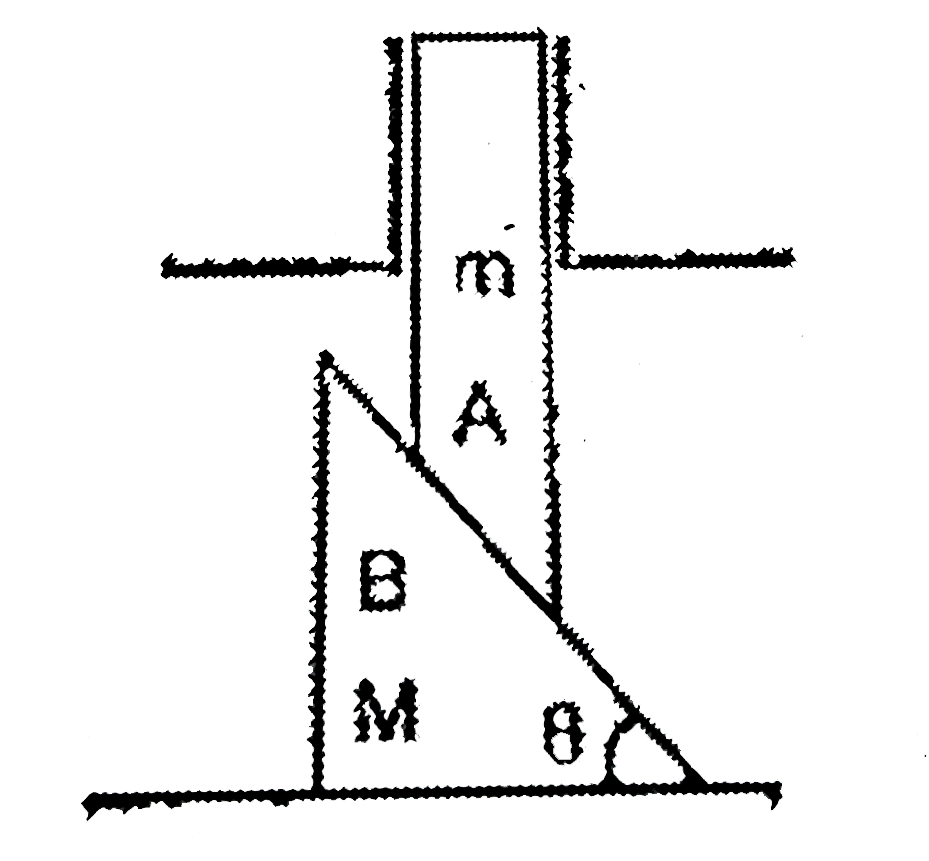
View Solution