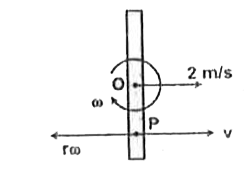
As shown in the figure, a rod moves with v = 2 m/sec & rotates with ω=2π rad/sec. Find the point on the rod whose velocity is zero in this frame.

vP=0
⇒ ∣→VPO+→vo=0
⇒ vPO−vO=0⇒ vPO=vo
where vO=v&vPO=(OP)ω
⇒ (OP)ω=v
⇒ OP=vω=22.π=1πm.
The point is located at 1π m down to the centre of mass.
Similar Questions
Shown in the figure is rod which moves with v=2ms−1 and rotates with ω=2πrads−1. Find the instantaneous axis of rotation.

View SolutionA rod has length 'l' and mass per unit length linearly increases from λ to 2λ as shown in figure. Rod rotates with constant angular velocity ω in a gravity free space. Find the tension (in Newton) in the rod at its middle point. (take ωl=2m/secandλ=3kg/m)

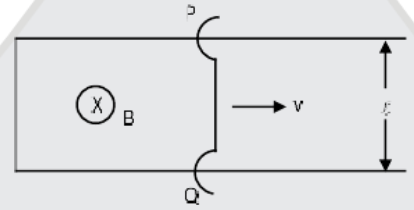
View SolutionA rod having length l and resistance R is moving with velocity v on a π shape conductor. Find the current in the rod.
View SolutionThe rod of length l=1m rotates with an angular velocity ω=2rads−1 an the point P moves with velocity v=1ms−1 and acceleration a=1ms−2. Find the velocity and acceleration of Q.

View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
View Solution
A uniform rod AB of mass m and length L rotates about a fixed vertical axis making a constant angle θ with it as shown in figure. The rod is rotated about this axis, so that point B the free end of the rod moves with a uniform speed V in the horizontal plane then the angular momentum of the rod about the axis is:
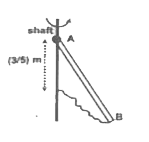
View SolutionA rod AB of length l = 1m and mass m = 2kg is pinned to a vertical shaft and a massless string is tied with the shaft at the lower end of the rod ( length of the string is 45m ) as shown in figure.If the shaft starts rotating with a constant angular velocity ω=5 rad / sec. Then find the tension in the string.
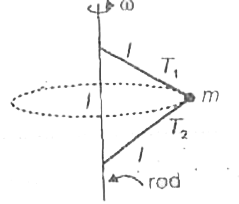
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
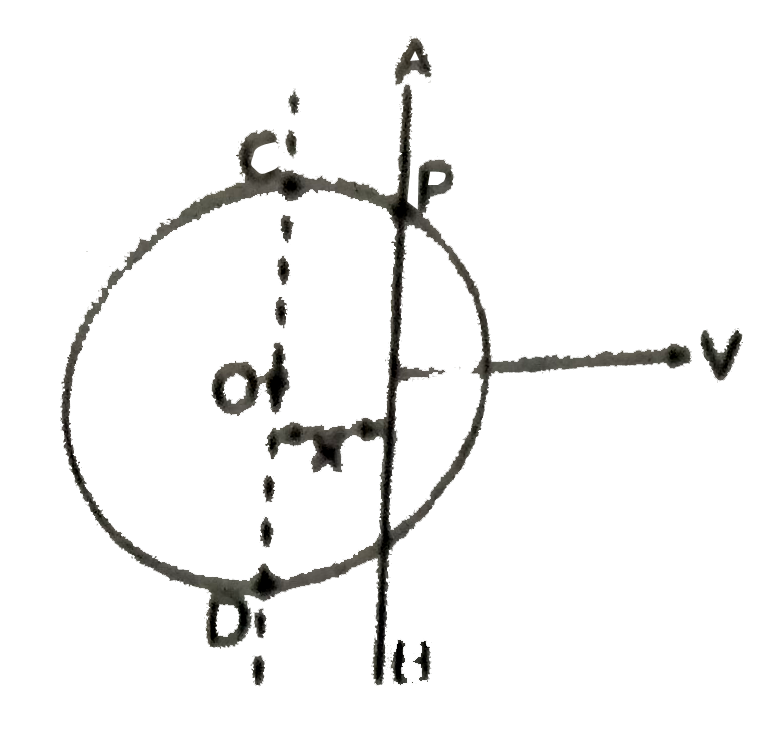
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View Solution
A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.
View Solution

