A ring of mass M and radius R lies in x-y plane with its centre at origin as shown. The mass distribution of ring is nun-uniform such that at any point P on the ring the mass per unit length is given by λ = λ0 cos2θ where λ0 is a positive constant. Then the moment of inertia of the ring about z-axis is –
Correct option: aExplanation:Divide the ring into infinitely small lengths of mass dm1 . Even though mass distribution is non-uniform each mass dm1 is at same distance R from origin.∴ MI of ring about z-axis isdm1R2 + dm2 R2 + .........+ dmnR2 = MR2
Related Solutions
A ring of mass and radius lies in plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point on the ring, the mass per unit length is given by (where is a positive constant). Then the moment of inertia of the ring about z-axis is :
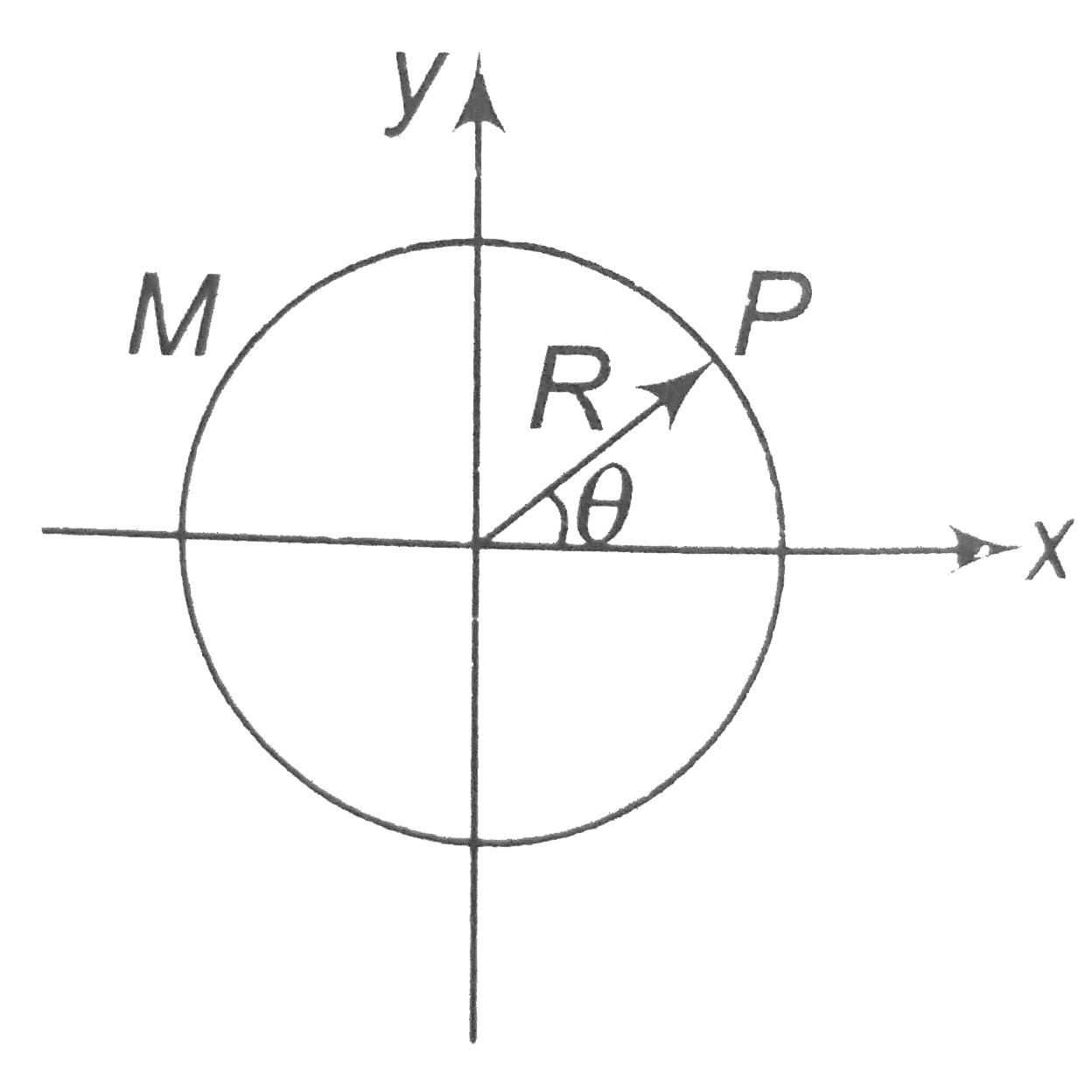 .
.
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass and radius about an axis which is tangent ot the ring and in the plane of the ring . perpendicular to the plane of the ring.
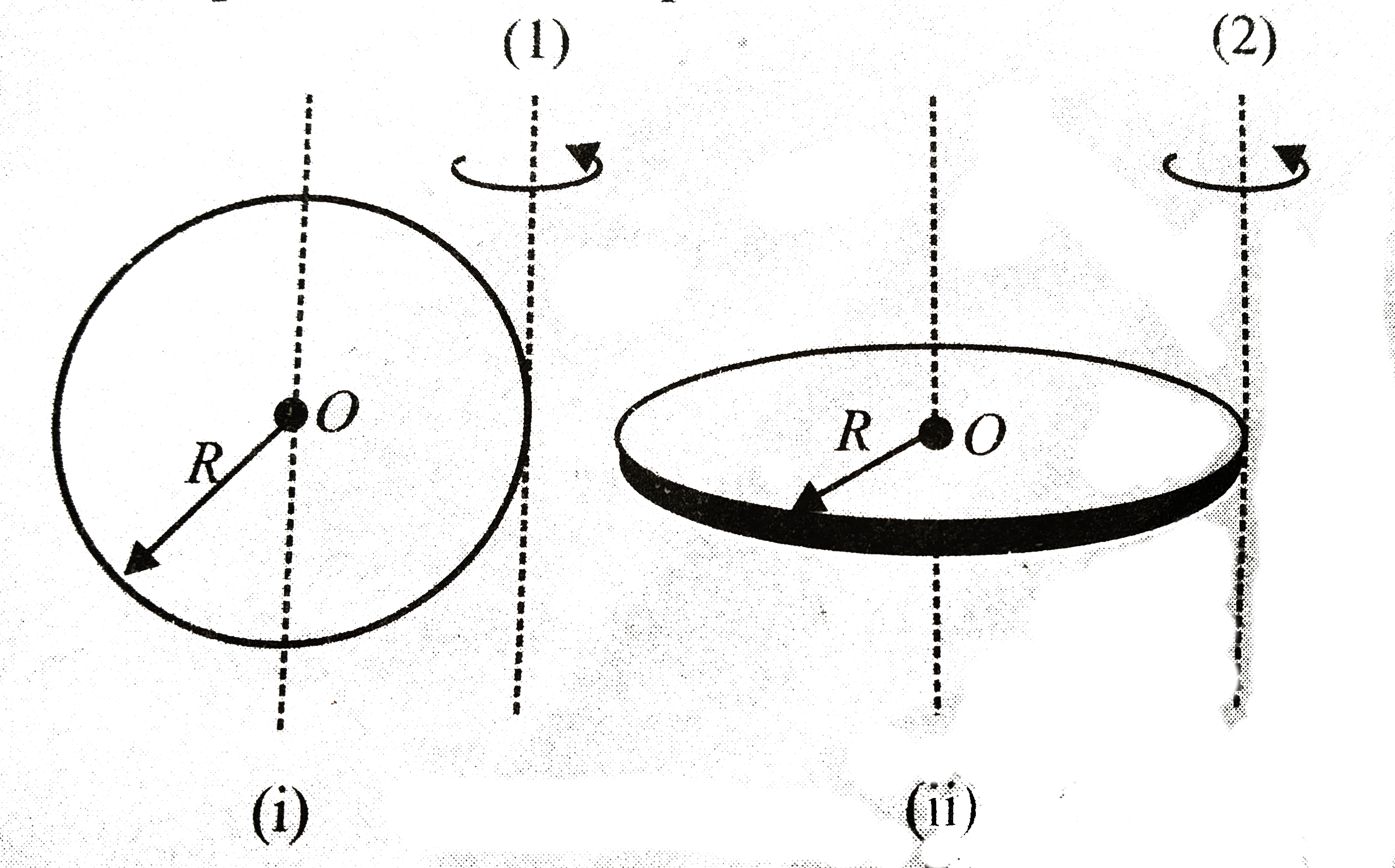
View SolutionFind the out the moment of inertia of a ring having uniform mass distribution of mass M and radius R about an axis which is tangent ot the ring and a in the plane of the ring b . perpendicular to the plane of the ring.
View SolutionCalculate the moment of inertia of a ring having mass , radius and having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
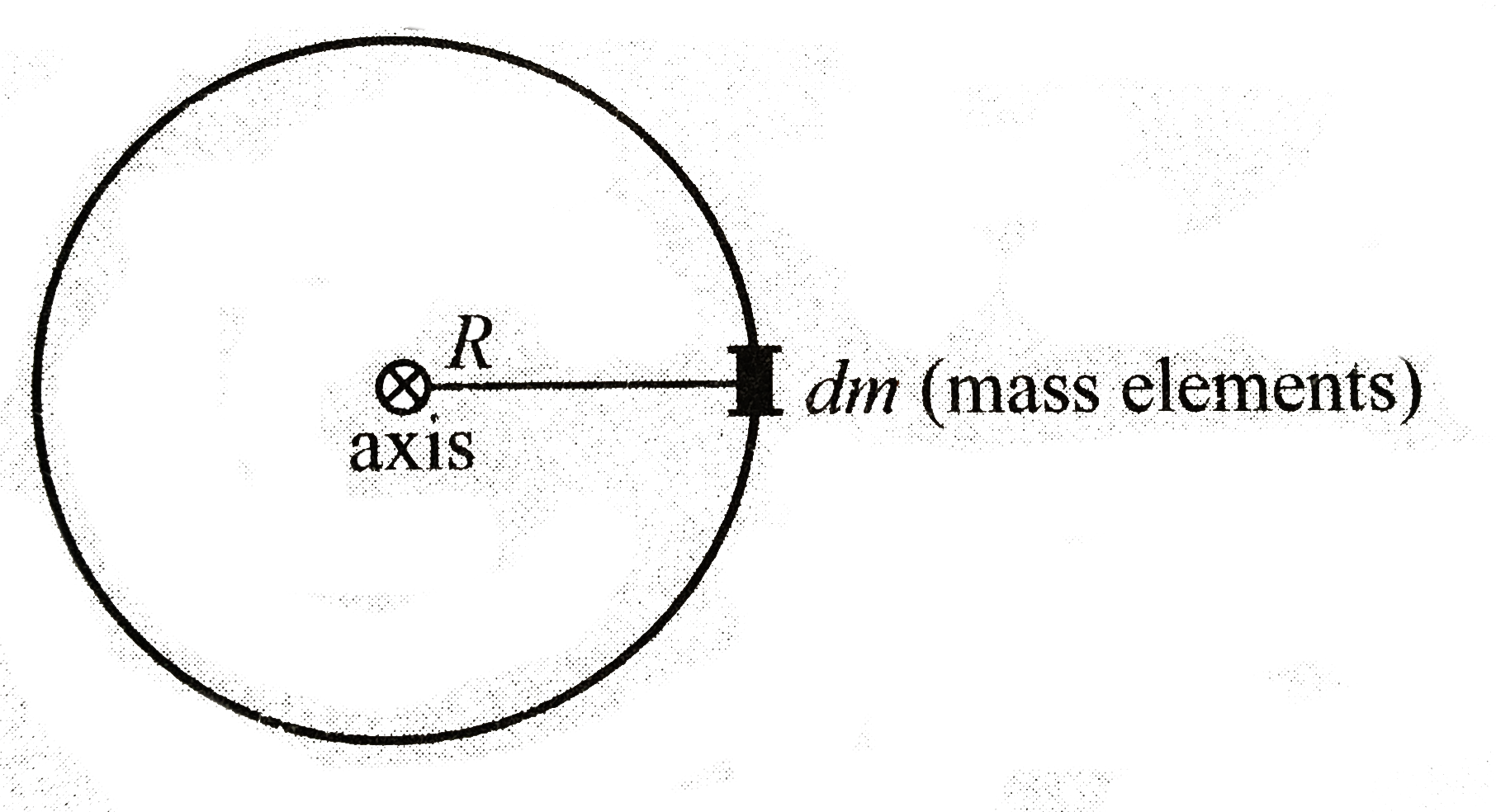
View SolutionCalculate the moment of inertia of a ring having mass M , radius R and having uniform mass distribution about an axis passing through the centre of the ring and perpendicular to the plane of the ring?
View SolutionThe moment of inertia of a uniform circular ring, having a mass M and a radius R, about an axis tangential to the ring and perpendicular to its plane, is
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be :-
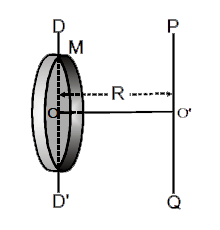
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be
View SolutionFrom a complete ring of mass M and radius R, an are of making 30^(0) at centre is removed. What is the moment of inertia of the incomplete ring about an axis passing through the centre of the ring and bot^(er) to the plane of the ring
View SolutionFrom a complete ring of mass M and radius R, an arc of making 30^(@) at centre is removed. What is the moment of inertia of the incomplete ring about an axis passing through the centre of the ring and bot^(er) to the plane of the ring
View SolutionFrom a complete ring of mass M and radius R, an are of making 30^(@) at centre is removed. What is the moment of inertia of the incomplete ring about an axis passing through the centre of the ring and _|_^(et) to the plane of the ring .
View Solutionत्रिज्या R तथा द्रव्यमान, M की वृत्तीय वलय में से द्रव्यमान M तथा त्रिज्या सूक्ष्म वलय को निकाल दिया जाता है वलय के लम्बवत् तथा उसकी अक्ष से गुजरने वाली अक्ष के परित: बचे हुये भाग का जड़त्व आघूर्ण है।
View SolutionThe centre of mass of a ring of uniform mass distribution lies ………….
View SolutionThe mass of a circular ring is and its radius is . Its moment of inertia about an axis in the plane of ring at perpendicular distance from centre of ring is
View SolutionMoment of inertia of a uniform circular ring of mass and radius about a diameter of ring is………………. .
View SolutionFind the moment of inertia of a ring of mass m and radius r about an axis passing through the tangent to the circle of the ring.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionFrom a complete ring of mass and radius , a sector is removed. The moment of inertia of the incomplete ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is
 ,
,
View Solution