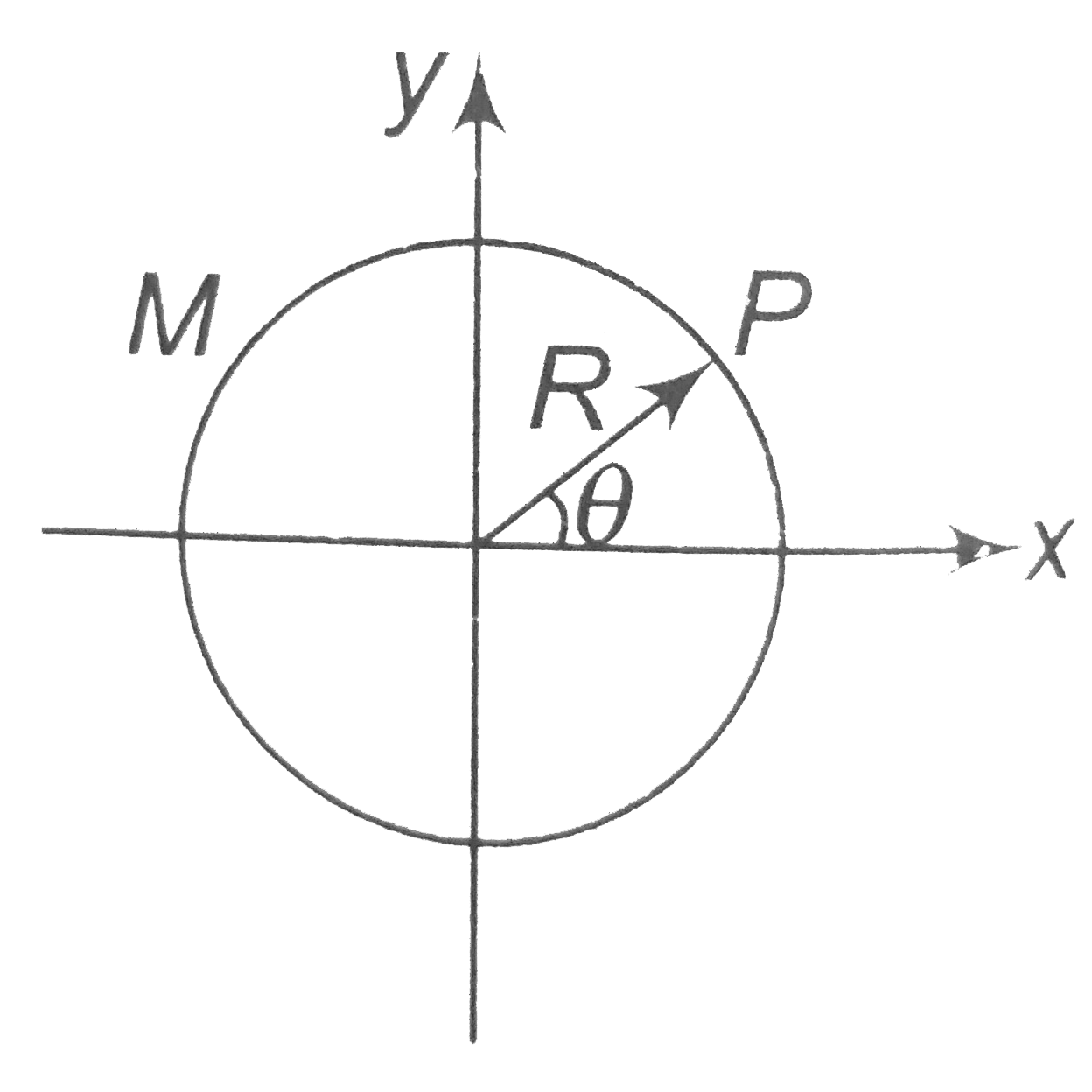
A ring of mass M and radius R lies in x−y plane with its centre at origin as shown. The mass distribution of ring is non uniform such that, at any point P on the ring, the mass per unit length is given by λ=λ0cos2θ (where λ0 is a positive constant). Then the moment of inertia of the ring about z-axis is :
 .
.
MR2
12MR2
12Mλ0R
1πMλ0R
The correct Answer is:A
(a) Divide the ring into infinitely small lengths of mass dmi. Even through mass distribution is non-uniform, each mass dmi is at same distance R from origin.
:. MI of ring about z-axis is
=dm2R+dm2R2+…+dmnR2=MR2.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotational Kinematics
Explore 19 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Torque , Torque Equation And Equilibrium Of A Rigid Body
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Displacement , Velocity And Acceleration Of Centre Of Mass
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A circular ring of mass M and radius R is placed in YZ plane with centre at origin. A particle of mass m is released from rest at a point x = 2R. Find the speed with which it will pass the centre of ring .
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View Solution
Knowledge Check
A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
AMl4π2BMl2πCMl4πDMl24π2A wire of mass m and length l is bent in the form of circular ring. The moment of inertia of the ring about its axis is
Aml2Bml24π2Cml22π2Dml28π2A wire of mass 'm' and length 'l' is bent in the form of a circular ring. The moment of inertia of the ring about its axis is-
Aml2B1ml22π2Cml24πDml28π2
The moment of inertia of a ring of mass M and radius R about PQ axis will be :-

View SolutionA ring of mass m and radius R is being rotated about its axis with angular velocity ω. If a increases then tension in ring
View SolutionA thin wire of mass M and length L is turned into a ring. The moment of inertia about its axis will be:
View SolutionA ring of mass M and radius R is at rest at the top of an incline as shown. The ring rolls down the plane without slipping. When the ring reaches bottom, its angular momentum about its centre of mass is:
View SolutionFor a uniform ring of mass M and radius R at its centre
View Solution

