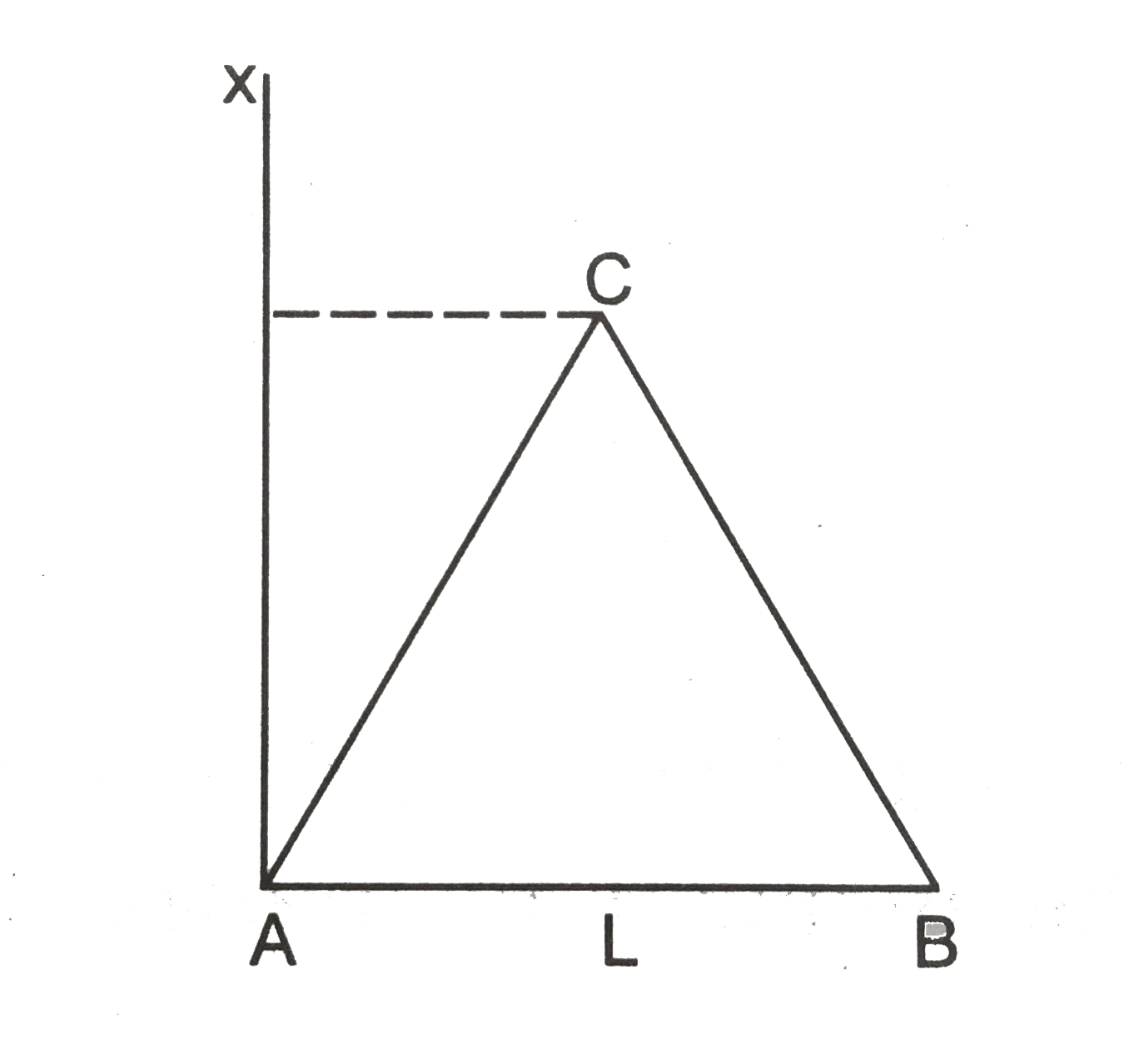
Figure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
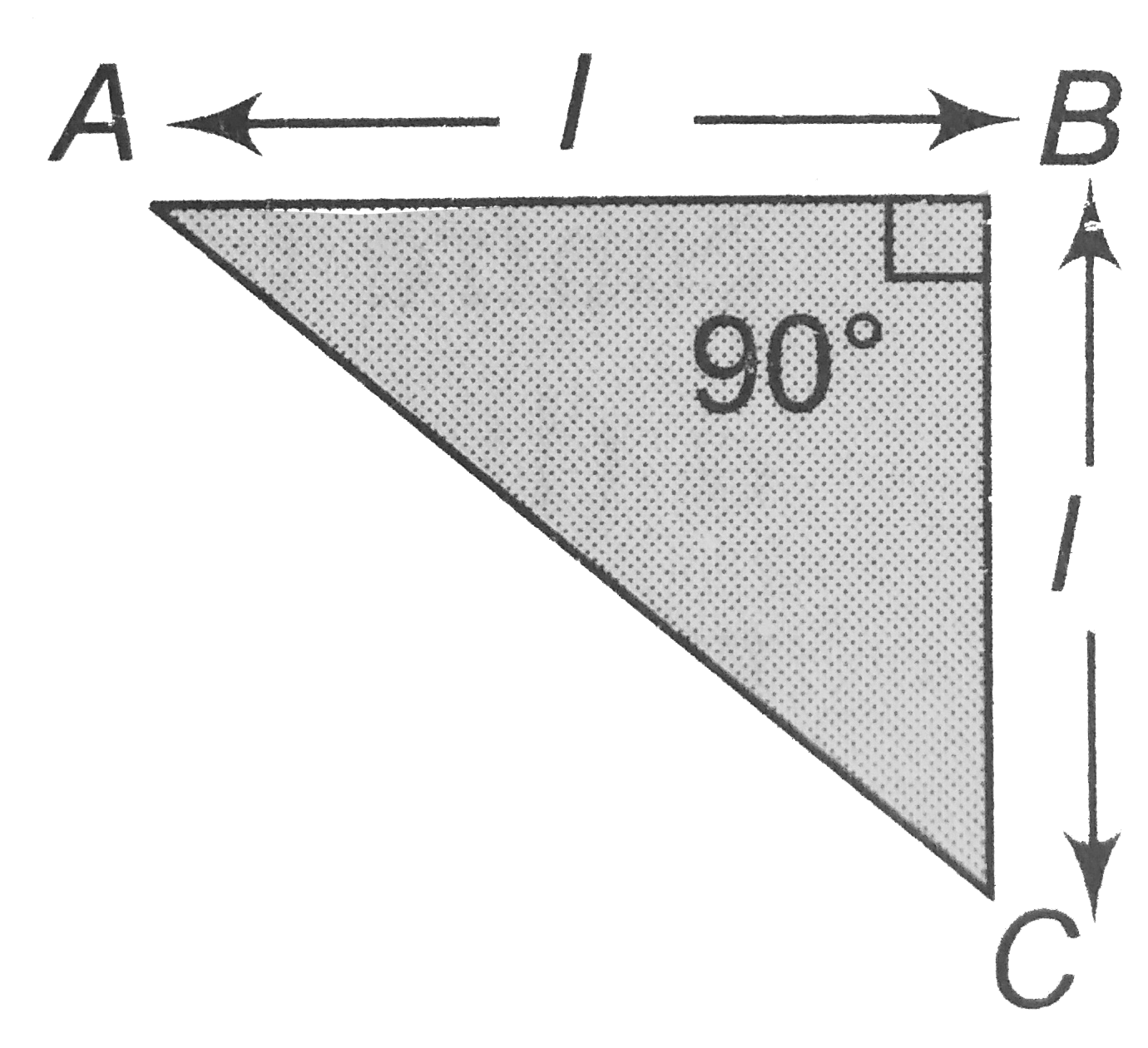 .
.
Ml218
Ml212
Ml26
Ml24
The correct Answer is:B
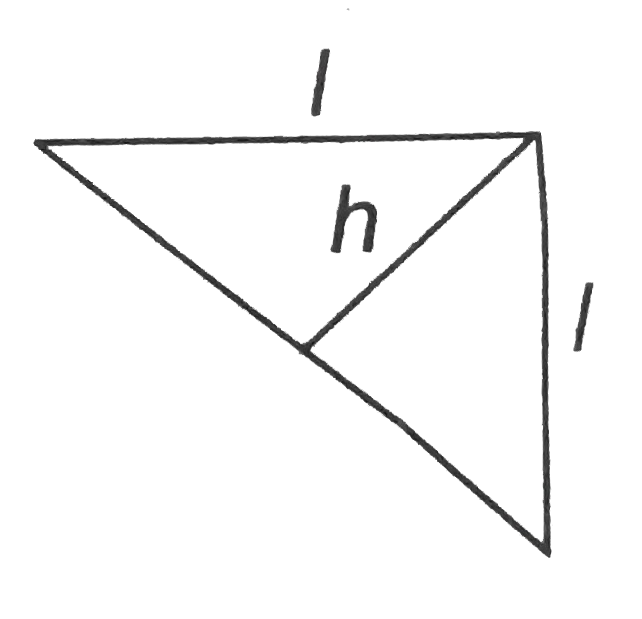
(b) h=l√2
IAC=16Mh2=Ml212.
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Rotational Kinematics
Explore 19 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Torque , Torque Equation And Equilibrium Of A Rigid Body
Explore 29 Videos
- ROTATIONAL DYNAMICSBook:A2ZChapter:ROTATIONAL DYNAMICSExercise:Displacement , Velocity And Acceleration Of Centre Of Mass
Explore 30 Videos
- PROPERTIES OF MATTERBook:A2ZChapter:PROPERTIES OF MATTERExercise:Chapter Test
Explore 29 Videos
- THERMAL PROPERTIES OF MATTERBook:A2ZChapter:THERMAL PROPERTIES OF MATTERExercise:Chapter Test
Explore 30 Videos
Similar Questions
A thin uniform metallic triangular sheet of mass M has sides AB=BC=L. What is its moment of inertia about axis AC lying in plane of sheet ?

View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
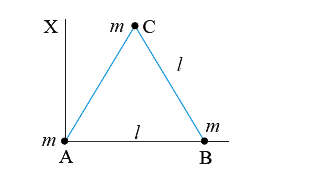
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution
Knowledge Check
In a metallic triangular sheet ABC, AB=BC=l. If M is mass of sheet, what is the moment of inertia about AC?
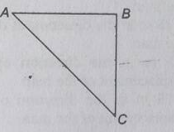 AMl24BMl212CMl26DMl218
AMl24BMl212CMl26DMl218In a metallic triangular sheet ABC, AB=BC=l. If M is mass of sheet, what is the moment of inertia about AC?
 AMl24BMl212CMl26DMl218
AMl24BMl212CMl26DMl218The circumference of a circular sheet is 154 m. The area of the sheet is equal to
A1886.5m2B1806.5m2C1886.5m2D1688.5m2
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
View SolutionThe moment of inertia of a triangular lamina of mass M about edge AB is equal to?
View SolutionAn equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I0 If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

View SolutionA uniform plane sheet of metal in the form of a triangle ABC has BC>AB>AC. Its moment of inertia will be smallest
View SolutionThe moment of inertia of a thin sheet of mass M of the given shape about the specified axis is

View Solution

