Consider figure shown a hemispherical cavity of radius R is curved out from a sphere μ = 1.5 of radius 2R such that the principal axis of the cavity coincides with that of the sphere. One side of the sphere is silvered as shown. Find the value of x for which the image of an object at O is formed at O itself
Related Solutions
A hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R ) as shown in the figure. Then
View SolutionA hemi-spherical cavity is created in solid sphere (of radius ) as shown in the figure. Then

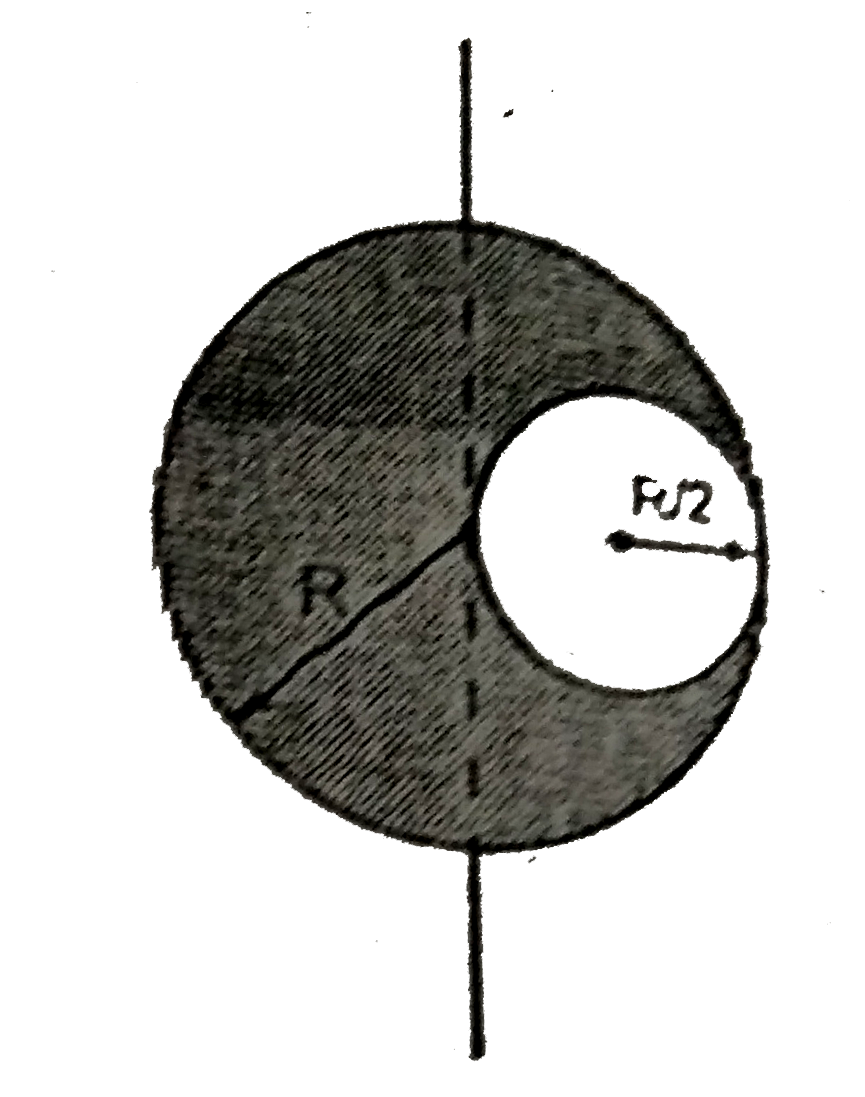
View SolutionA spherical cavity is formed a solid sphere by removing mass from it. The resultant configuration is shown in figure. Find out the moment of inertia this configuration about the axis through centre of the solid sphere as shown . Take mass uniform for the configuration and radius for solid sphere and radius for cavity.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution- A glass sphere of refractive index mu 2.4 has one half silvered. A point object O is placed in front of the sphere at a distance d as shown in the figure. The value of d for which image of O is coinciding with the object O itself is given by d = kR then value of K will be? Consider paraxial rays approximation to be valid.
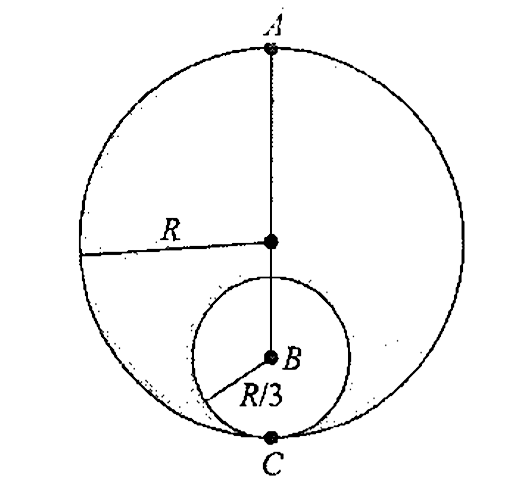
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius , is made in the sphere as shown :
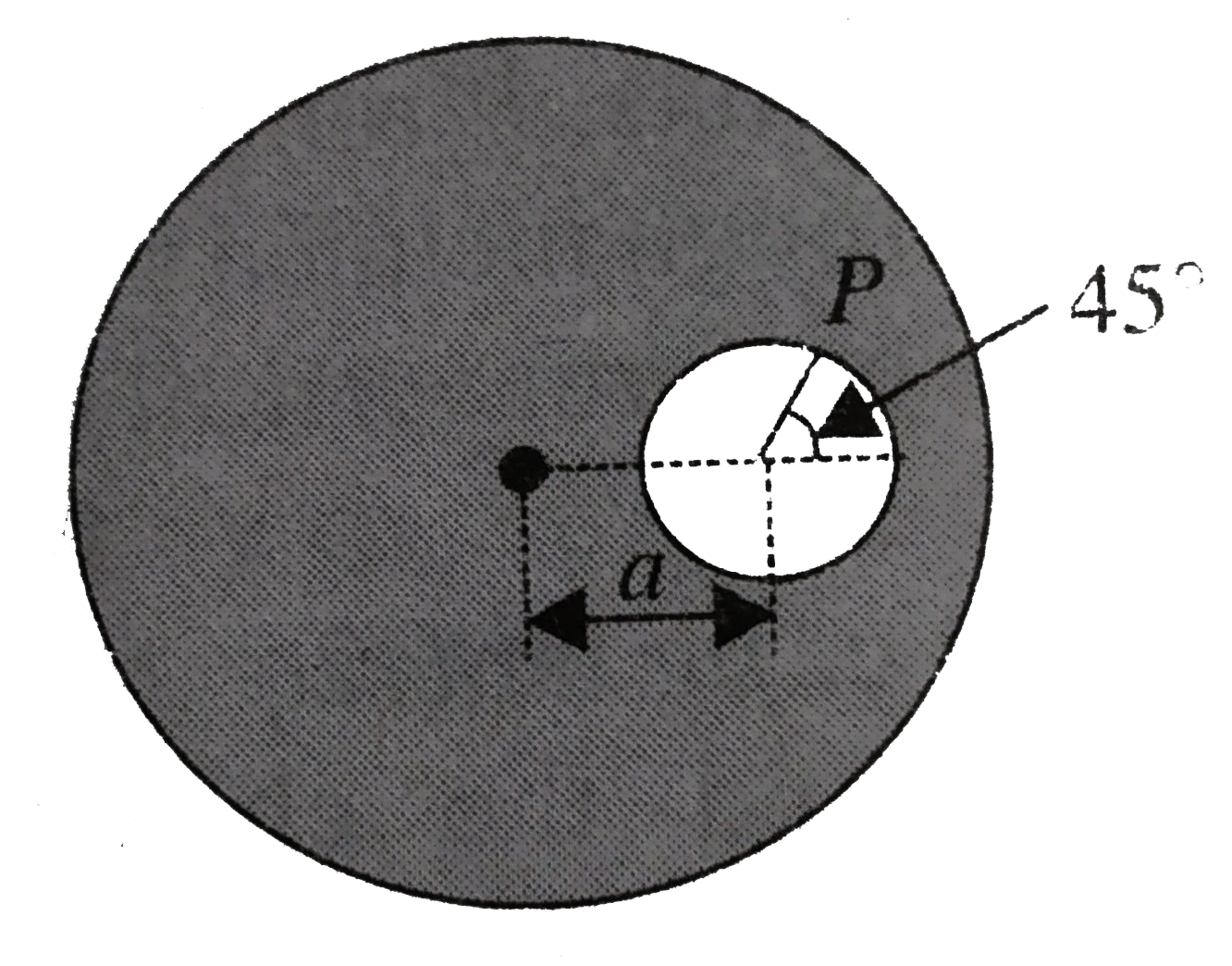
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is p. An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and centre of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is rho . An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View SolutionA cavity of radius r is made inside a solid sphere. The volume charge density of the remaining sphere is . An electron (charge e, mass m) is released inside the cavity from point P as shown in figure. The centre of sphere and center of cavity are separated by a distance a. The time after which the electron again touches the sphere is
View Solutionद्रव्यमान M और त्रिज्या R के एक ठोस गोले में, त्रिज्या की एक गोलीय गुहिका इस प्रकार बनाई गई है कि गुहिका का केंद्र गोले के केंद्र से से दूरी पर है। एक बिंदु द्रव्यमान m को गोले के केंद्र से की दूरी पर गुहिका के अंदर रखा जाता है। गोले और बिंदु द्रव्यमान m के बीच गुरुत्वाकर्षण खिंचाव है
View Solution
consider a neutral conducting sphere of radius with a spherical cavity of radius . A charged conducting sphere of radius is placed in cavity . Centre of this sphere coincide with centre of cavity charge on the inner sphere is total self energy of this arrangement is:
View Solutionconsider a neutral conducting sphere of radius a with a spherical cavity of radius b . A charged conducting sphere of radius c is placed in cavity . Centre of this sphere coincide with centre of cavity charge on the inner sphere is q total self energy of this arrangement is:
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
View SolutionAs shown in figure, when a spherical cavity (centered at O) of radius 2 is cut out of a uniform sphere of radius R (centered at C), the centre of mass of remaining (shaded) part of sphere is at G, i.e, on the surface of the cavity. R can be determined by the equation:
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density sigma is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
View SolutionA solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density sigma is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
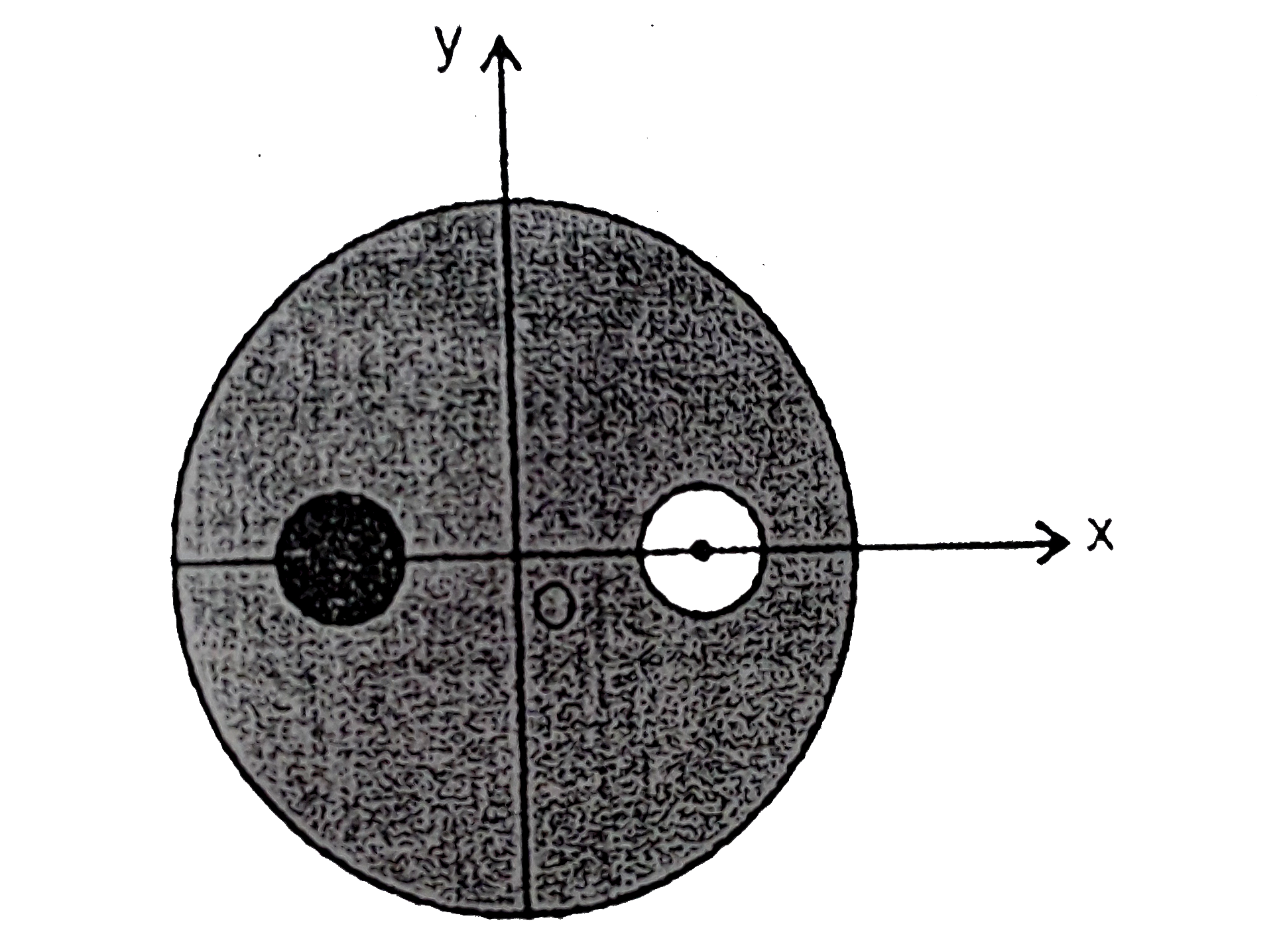
View SolutionConsider a solid sphere of density and radius . Centre of the sphere is at origin. Two spherical cavities centred at and are created in sphere. Radii of both cavities is . In left cavity material of density is filled while second cavity is kept empty. What is gravitational field at origin.
View Solution