A uniform disc of radius R and mass M is attached to the end of a uniform rigid rod of length L and mass m. When the disc is suspended from a pivot as shown in Fig. 1.32 what will be the period of motion?
The equation of motion is Γ = Iα where Γ is the external torque I is the moment of inertia α is the angular acceleration and both Γ and I are about the pivot point. Let θ be a small angular displacement from the vertical. Now external torque comes both from the rod and the disc:
Related Solutions
A thin rod of length l and mass m has a disc attached to one of its end such that rod and disc are coplanar. Mass of the disc is M and radius is r. C.M. from the cenre of disc is
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA uniform circular disc of mass M and radius R is pivoted at distance x above the centre of mass of the disc, such that the time period of the disc in the vertical plane is infinite. What is the distance between the pivoted point and centre of mass of the disc ?
View SolutionA metal rod of length 'L' and maws 'm' is pivoted at one end A thin disc of mass 'M' and radius 'R' ( Which of the folowing statement (s) is (are) true ?
View SolutionFind the time period of small oscillations of the following systems.
(a) A uniform rod of mass m and length L is suspended through a pin hole at distance from top as shown.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform disc of mass m and radius r suspended through a point away from centre.
(d) A uniform square plate of edge a suspended through a corner.
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
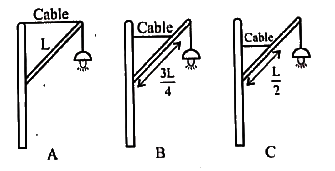
View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then

View SolutionIf a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then:
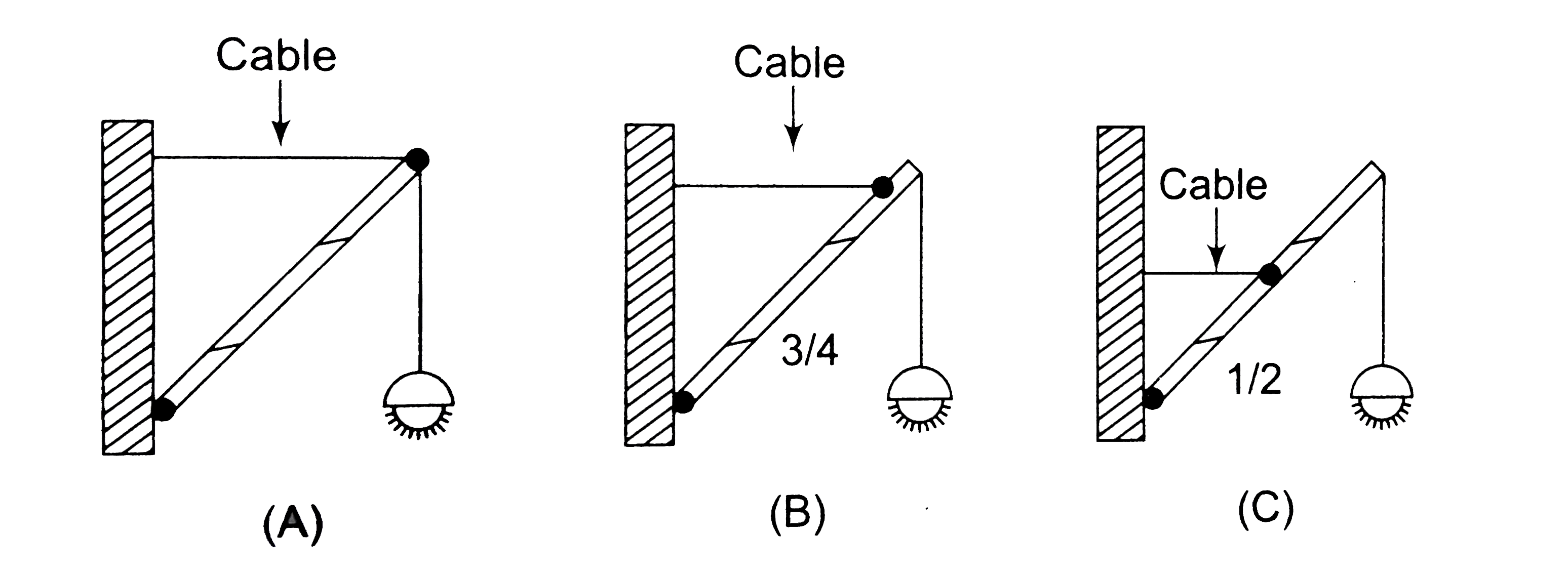
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :
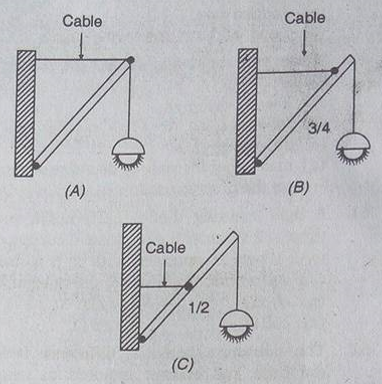
View SolutionIn a street light of mass M is suspended from the end of a uniform rod of length L in different possible patterns as shown in figure, then :

View SolutionA system of uniform rod of mass m and length 2R and a uniform disc of m and radius R are as shown in the figure. The moment of inertia of the system about the axis (perpendicular to plane of disc) will be
View Solution
A uniform disc of mass m and radius m is pivoted smoothly at . If a uniform disc of mass and radius is welded at the lowest point of the disc, find the period of of the system (disc ring). (in seconds)
View Solution
A uniform dics of mass m and radius m is pivoted smoothly at . If a uniform disc of mass and radius is welded at the lowest point of the disc, find the period of of the system (disc ring). (in seconds)
View SolutionA uniform disc of mass m and radius R has an additional rim of mass m as well as four symmetrically placed masses, each of mass m//4 tied at positions R//2 from the centre as shown in Fig. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?
View SolutionA uniform disc of mass and radius has an additional rim of mass as well as four symmetrically placed masses, each of mass tied at positions from the centre as shown in Fig. What is the total moment of inertia of the disc about an axis perpendicular to the disc through its centre?

View SolutionA disc of radius a is ridigly attached at its circumference to a rod of length 3a and the combination suspeded vertically from the other end of the rod. It is swinging in the plane of the disc such that the centre of disc has velocity v . If mass of disc and rod is m
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius (R)/(2) is removed from it. Then choose the correct option(s)
View SolutionA uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius (R)/(2) is removed from it. Then choose the correct option(s)
View Solution