A bead of mass m slides on a frictionless wire of nearly parabolic shape Fig. 1.31. Let the point P be the point at the bottom of the wire. Show that the bead will oscillate about P if displaced slightly from P and released.
Since the shape of the wire near P is a parabola the potential energy of the bead is given by V = cx2 in the neighbourhood of P where x is measured from P and c is a constant. Now and directed opposite to the direction of increasing x. So the bead executes SHM and its time period is given by Note that this line of reasoning leads to a general result: Any conservative system will oscillate with SHM about a minimum in its potential energy curve provided the oscillation amplitude is small enough.
Related Solutions
A bead of mass m can side on a frictionless wire as shown in figure Bacause of the given shape of the wire near p the bottom point , it can be approximatedd as abola near p the potential energy of the bead is given U = cx^(2) where c is a constant and x is measured from p The bead if displacvement slighly from point p will oscillate about p The period of oscillation is
View SolutionA wire which is bent in the shape of a curve given by, . A bead of mass m is located at point P(x,y). If the wire is smooth, find with which wire needs to be rotated for bead to be static.
View SolutionA wire which is bent in the shape of a curve given by, . A bead of mass m is located at point P(x,y). If the wire is smooth, find with which wire needs to be rotated for bead to be static.
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is . The wire frame is fixed and the bead is released from the point on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is . The wire frame is fixed and the bead is released from the point on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x^(2) =4ay . The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View SolutionA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the vertical line is
View SolutionA bead of mass m slides down a frictionless thin fixed wire held on the vertical plane and then performs small oscillations at the lowest point O of the wire. The wire takes the shape of a parabola near O and potential energy is given by U (x)= cx^(2) , where c is a constant. The period of the small oscillations will be :
View SolutionA bead of mass m slides down a frictionless thin fixed wire held on the vertical plane and then performs small oscillations at the lowest point O of the wire. The wire takes the shape of a parabola near O and potential energy is given by U (x)= cx^(2) , where c is a constant. The period of the small oscillations will be :
View SolutionA small bead of mass m can moves on a smooth circular wire (radiusR) under the action of a force directed (r=position of bead from P&K=constant) towards a point P with in the circle at a distance from the centre what should be the minimum velocity of bead at the point of the wire nearest the centre of force (P) so that bead will complete the circle

View SolutionA bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass then when the string makes an angle with the wire, the bead will have slipped a dsitance.

View SolutionA bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a dsitance.
View SolutionA bead can slide on a smooth straight wire and a particle of mass m attached to the bead by a light string of length L . The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a distance.
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equations is . The wire frame is fixed and the bead can slide on it without friction . The bead is released from the point y = 4a on the wire frame from rest . The tangential acceleration of the bead when it reaches the position given by y = a is :

View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the verticle line is
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the verticle line is
View SolutionThe Fig. shows a string of equally placed beads of mass , separated by distance . The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,
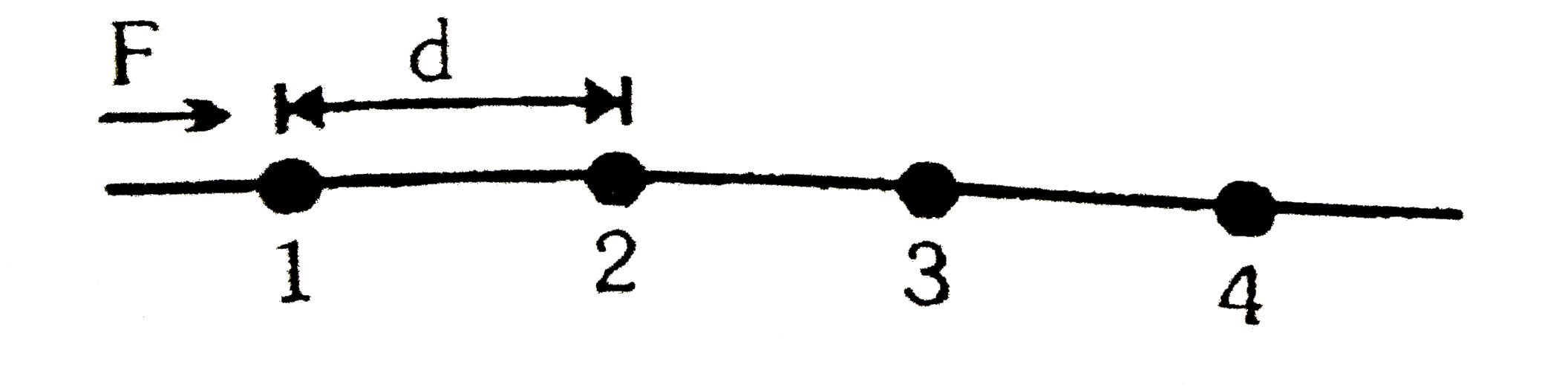
View SolutionThe Fig. shows a string of equally placed beads of mass , separated by distance . The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,

View Solution