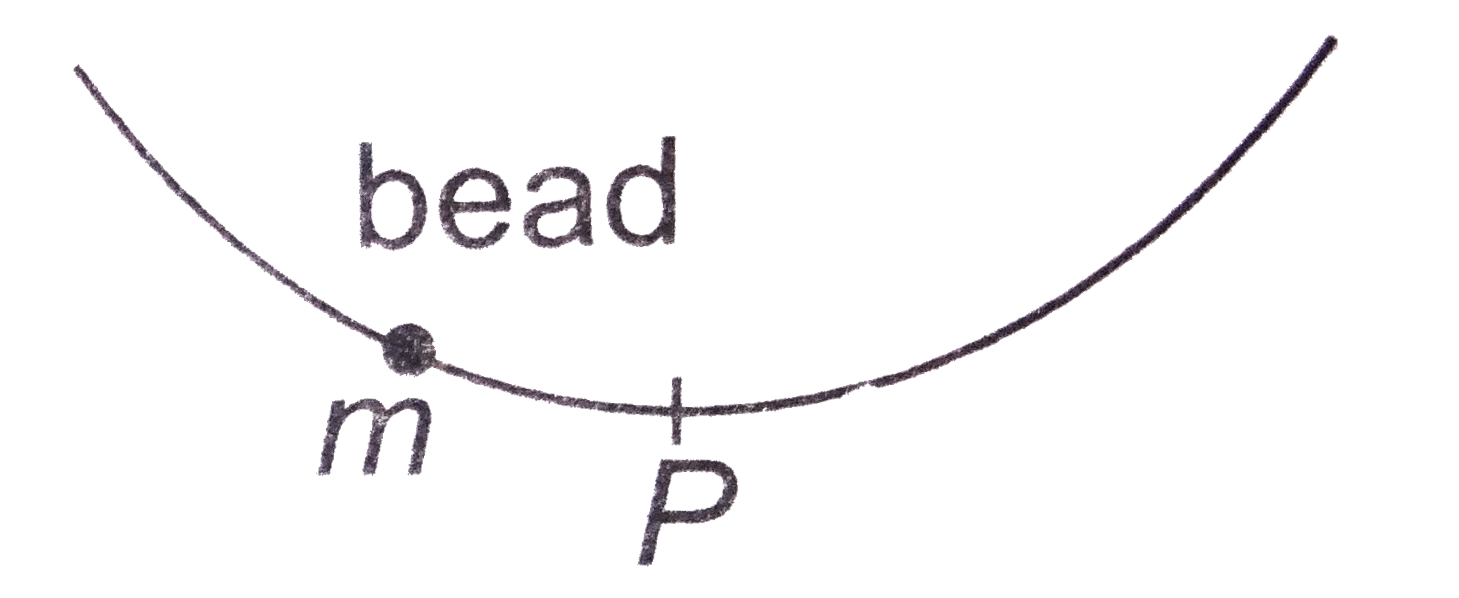
A bead of mass m can slide on a frictionless wire as shown in figure Because of the given shape of the wire near p the bottom point , it can be approximated as near p the potential energy of the bead is given U=cx2 where c is a constant and x is measured from p The bead if displacement slightly from point p will oscillate about p The period of oscillation is
2π√c/m
2π√m/2c
2π√m/c
2π√2c/m
The correct Answer is:B
U=Cx2
F=−dUdx⇒ma=−2cx⇒a=−2cmx
⇒ω=√2cm⇒T=2πω=2π√m2c
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
22 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - NEET Questions
39 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum
19 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
The potential energy of a particle of mass m is given by U(x)=U0(1−coscx) where U0 and c are constants. Find the time period of small oscillations of the particle.
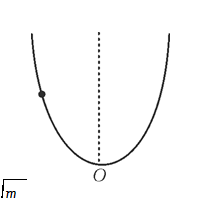
View SolutionA bead of mass m slides down a frictionless thin fixed wire held on the vertical plane and then performs small oscillations at the lowest point O of the wire. The wire takes the shape of a parabola near O and potential energy is given by U (x)=cx2, where c is a constant. The period of the small oscillations will be :
View Solution
Knowledge Check
A bead of mass m can slide on a frictionless wire as shown in figure Because of the given shape of the wire near p the bottom point , it can be approximated as near p the potential energy of the bead is given U=cx2 where c is a constant and x is measured from p The bead if displacement slightly from point p will oscillate about p The period of oscillation is
 A2π√c/mB2π√m/2cC2π√m/cD2π√2c/m
A2π√c/mB2π√m/2cC2π√m/cD2π√2c/mBorax bead test is given by
ACo2+BZn2+CCu2+DNi2+Borax bead test is given by :
ACo2+BZn2+CCu2+DNi2+
Borax bead test is given by:
View SolutionA particle of mass m oscillates with a potential energy U=U0+αx2, where U0 and α are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View SolutionBorax bead test is not given by
View SolutionBorax bead test is not given by
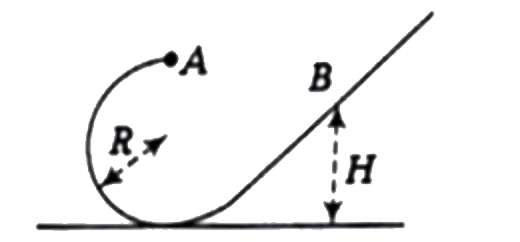
View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
View Solution
