Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
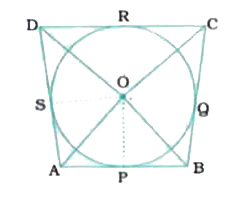
Solution: Let ABCD be a quadrilateral circumscribing a circle with O such that it touches the circle at point P Q R S. Join the vertices of the quadrilateral ABCD to the center of the circle.In ΔOAP and ΔOAS AP = AS Tangents from the same pointOP = OS Radii of the circleOA = OA Common sideΔOAP ≅ ΔOAS SSS congruence condition∴ ∠POA = ∠AOS⇒∠1 = ∠8Similarly we get ∠2 = ∠3∠4 = ∠5∠6 = ∠7Adding all these angles ∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 +∠8 = 360º⇒ ∠1 + ∠8 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 = 360º⇒ 2 ∠1 + 2 ∠2 + 2 ∠5 + 2 ∠6 = 360º⇒ 2∠1 + ∠2 + 2∠5 + ∠6 = 360º⇒ ∠1 + ∠2 + ∠5 + ∠6 = 180º⇒ ∠AOB + ∠COD = 180ºSimilarly we can prove that ∠ BOC + ∠ DOA = 180ºHence opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Related Solutions
Prove that the opposite sides of a quadrilateral circumscribing a
circle subtend supplementary angles at the centres of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle .
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposites of a quadrilaterial circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that opposites of a quadrilaterial circumscribing a circle subtend supplementary angles at the centre of the circle.
View SolutionProve that for a quadrilateral circumscribed about a circle, the angles subtended by any two opposite sides at the centres are supplementary to each other.
View SolutionProve that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
View SolutionProve that opposite side of a quadrilateral circumscribing a circle subtend supple. Mentary angle at the center of the circle.
View SolutionA circle touches the sides of a quadrilateral at respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
View SolutionA circle touches the sides of a quadrilateral at respectively. Show that the angles subtended at the centre by a pair of opposite sides are supplementary.
View Solutionएक वृत्त एक चतुर्भुज की सभी भुजाओ को स्पर्श करता है। सिद्ध कीजिए कि केंद्र पर सम्मुख भुजाओ द्वारा अन्तरित कोण सम्पूरक होते है।
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View SolutionIf bisectors of opposite angles of a cyclic quadrilateral ABCD intersect the circle, circumscribing it at the points P and Q, prove that PQ is a diameter of the circle.
View Solution