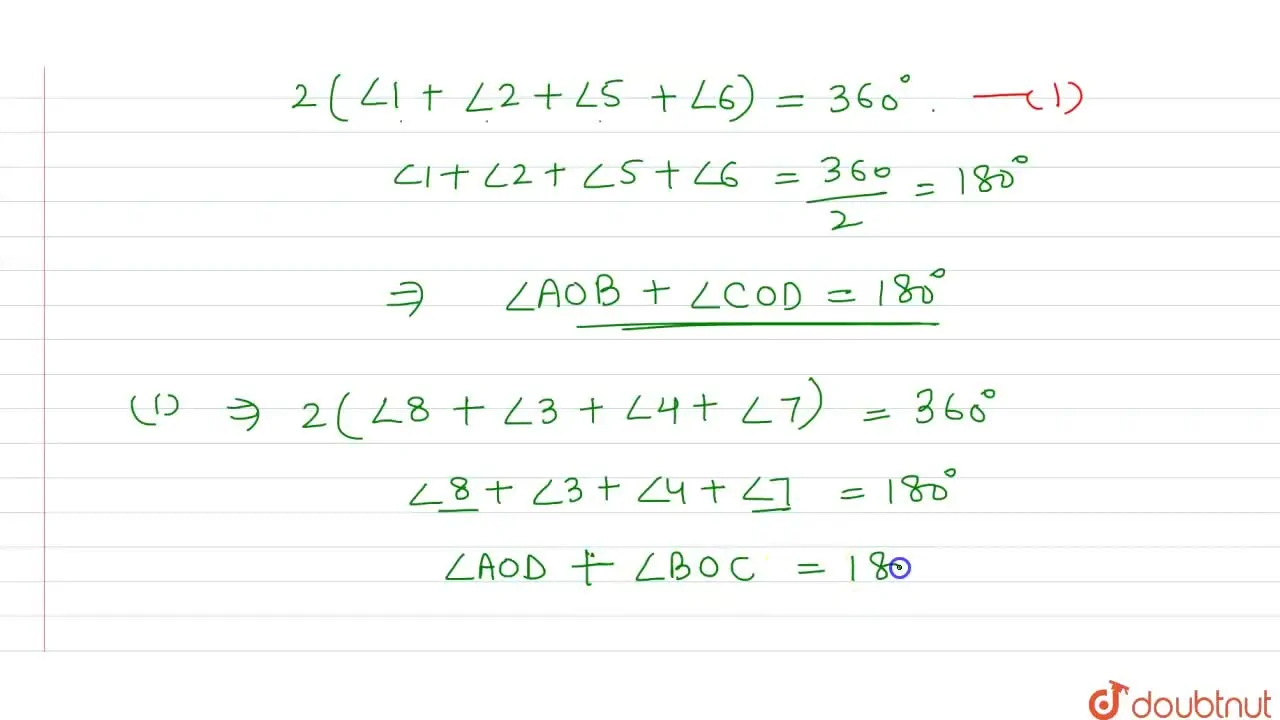Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Let ABCD be a quadrilateral circumscribing a circle with center O such that it touches the circle at point P,Q,R,S.
Join the vertices to the center of the circle.
In △OAP and △OAS,
AP=AS(Tangents from the same point)
OP=OS (Radii of the circle)
OA=OA (Common side)
△OAP≅△OAS
(SSS congruence condition)
∠POA=∠AOS
∠1=∠8
Similarly we get,
∠2=∠3
∠4=∠5
∠6=∠7
Adding all these angles,
∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=360∘
(∠1+∠8)+(∠2+∠3)+(∠4+∠5)+(∠6+∠7)=360∘
2∠1+2∠2+2∠5+2∠6=360∘
2(∠1+∠2)+2(∠5+∠6)=360∘
(∠1+∠2)+(∠5+∠6)=180∘
∠AOB+∠COD=180∘
Similarly, we can prove that
∠BOC+∠DOA=180∘
Hence, opposite sides of quadrilateral subtend supplementary angles at the center of the circle.
Similar Questions
Prove that opposite sides of a quadrilateral circumscribing a circle, subtend supplementary angles at the centre of a circle.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionState and prove that :
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centreView SolutionIf a Quardlateral is circumscribed of a circle and ∠AOB is 135∘ find angle COD . O is the centre of circle
View SolutionProve that the rectangle circumscribing a circle is a square
View SolutionConsider the following statements
1. the opposite angles of a cyclic quadrilateral are supplementary.
2. Angle subtended by an arc at the centre is doubled the angle subtended by it any point on the remaining part of the circle.
Which one of the following is correct in respect of the above statementsView SolutionEqual chord of circle subtends equal angle on centre.
View Solution