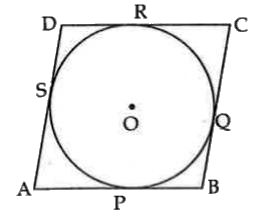
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:ABCD is a parallelogram ∴ AB = CD ... i∴ BC = AD ... iiFrom the figure we observe that DR = DS Tangents to the circle at DCR = CQ Tangents to the circle at CBP = BQ Tangents to the circle at BAP = AS Tangents to the circle at AAdding all these DR + CR + BP + AP = DS + CQ + BQ + AS⇒ DR + CR + BP + AP = DS + AS + CQ + BQ⇒ CD + AB = AD + BC ... iiiPutting the value of i and ii in equation iii we get 2AB = 2BC⇒ AB = BC ... ivBy Comparing equations i ii and iv we get AB = BC = CD = DA∴ ABCD is a rhombus.
Related Solutions
Prove that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a rhombus.
View SolutionProve that the parallelogram circumscribing a circle is a Rhombus.
View SolutionProve that parallelogram circumscribing a circle is a rhombus.
View SolutionIf a parallelogram circumscribes a circle then prove that it must be a rhombus.

View SolutionIf a parallelogram circumscribes a circle then prove that it must be a rhombus.

View SolutionProve that the parallelogram circumscribed about a circle is only a rhombus.
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View SolutionIf all the side of a parallelogram touch a circle, show that the parallelogram is a rhombus. OR Prove that a parallelogram circumscribing a circle is a rhombus.
View Solutionसिद्ध कीजिए किसी वृत्त के परिगत समांतर चतुर्भुज समचतुर्भुज होता है।
View SolutionIf the sides of a parallelogram touch a circle prove that the parallelogram is a rhombus.
View SolutionIf the sides of a parallelogram touch a circle, prove that parallelogram is a rhombus.
View Solution