Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Solution:Consider a circle with centre O. Let P be an external point from which two tangents PA and PB are drawn to the circle which are touching the circle at point A and B respectively and AB is the line segment joining point of contacts A and B together such that it subtends ∠AOB at center O of the circle.It can be observed thatOA ⊥ PA∴ ∠OAP = 90°Similarly OB ⊥ PB∴ ∠OBP = 90°In quadrilateral OAPB Sum of all interior angles = 360º∠OAP +∠APB +∠PBO +∠BOA = 360º⇒ 90º + ∠APB + 90º + ∠BOA = 360º⇒ ∠APB + ∠BOA = 180º∴ The angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Related Solutions
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve tht the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
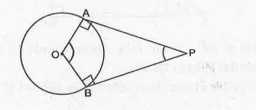
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line - segment joining the points of contact at the centre.
View SolutionProve that the angle between the two tangents drawn from an external point are supplementary to the angle subtended by the line segment joining the centre.
View SolutionProve that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line -segment joinig the point of contact at the centre.
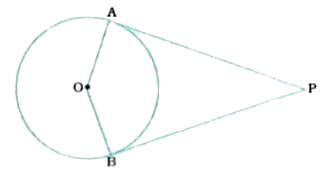
View SolutionWhat is the angle between the two tangents drawn from an external point to a circle and the angle subtended by the line-segment joining the points of the contact at the centre.
View SolutionProve that if two tangents are drawn to a circle from a point outside it, then the line segments joining the point of contact and the exterior point are equal and they subtend equal angles at the centre.
View Solutionसिद्ध कीजिये की किसी बाह्म बिंदु से वृत्त पर खींची गई दो स्पर्श रेखाओं के बीच का कोण स्पर्श बिंदुओं को मिलाने वाली रेखाखंड के केंद्र पर अंतरित (बनने वाला) कोण का सम्पूरक होता हैं|
View Solution