A ball of mass M attached to a string of length L moves in a circle in a vertical plane as shown. At the top of the circular path the tension in the string is twice the weight of the ball. At the bottom the ball just clears the ground. Air resistance is negligible. Express all answers in terms of M L and g. a. Determine the magnitude and direction of the net force on the ball when it is at the top. b. Determine the speed vo of the ball at the top. The string is then cut when the ball is at the top. c. Determine the time it takes the ball to reach the ground. d. Determine the horizontal distance the ball travels before hitting the ground.
a. At the top of the path tension and gravity apply forces downward toward the center of the circle.ΣF = T + mg = 2Mg + Mg = 3Mg
Related Solutions
A small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in the string at the highest point is twice the weight of the ball then (assume that the ball completes the vertical circle)
View SolutionA ball of mass m is fastened to a string. The ball swings in a vertical circle of radius R with the other end of the string held fixed. Neglecting the air resistance, the difference between the string's tension at the bottom of the circle and at the quarter of the cirlce is
View SolutionA ball of mass m is fastened to a string. The ball swings in a vertical circle of radius R with the other end of the string held fixed. Neglecting the air resistance, the difference between the string's tension at the bottom of the circle and at the quarter of the cirlce is
View SolutionA ball of mass m is attached to a light string of length L and suspended vertically. A constant horizontal force, whose magnitude F equals the weight of the ball, is applied Determine the speed of the ball as it reaches the level.
View SolutionA ball attached to one end of a string is rotated on a horizontal circular path about a vertical axis. Given that the maximum angular velocity of the ball is 42rads^(-1) a mass (m) of the ball is 0.8 kg, and length (l) of the string is 0.4m. String can bear maximum tension is Kxx10^(2) then K is
View SolutionA small spherical ball is suspended through a string of length l . The whole arrangement is placed in a vehicle which is moving with velocity v . Now, suddenly the vehicle stops and ball starts moving along a circular path. If tension in ht estring at the highest pointn is twice the weight of the ball then (assume that the ball completes the vertical circle)
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in radian/s) is:
View SolutionA ball of mass is attached to the end of a string having length . The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is . The maximum possible value of angular velocity of ball (in radian//s) is -
 .
.
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m . The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N . The maximum possible value of angular velocity of ball ( radian//s) is - .
View SolutionA ball of mass (m) 0.5 kg is attached to the. end of a string having length (L) 0.5 m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N. The maximum possible value of angular velocity of ball (in radian/s) is
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m . The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N . The maximum possible value of angular velocity of ball (in radian//s) is - .
View SolutionA ball of mass (m) 0.5 kg is attached to the end of a string having length (L) 0.5 m . The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324 N . The maximum possible value of angular velocity of ball (in radian//s) is - .
View SolutionA ball of mass 0.25 kg attached to the ends of a string of length 1.96 m is rotating in a horizontal circle . The string will break ,l if tension is more than 25 N . What is the maximum velocity with which the ball can be rotated ?
View SolutionA ball of mass (m) 0.5g is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
View SolutionA ball of mass (m) 0.5kg is attached to the end of a string having length (L) 0.5m. The ball is rotated on a horizontal circular path about vertical axis. The maximum tension that the string can bear is 324N. The maximum possible value of anguar velocity of ball(in radian/s) is
View SolutionA ball of mass .m. is rotated in a vertical by a string. The difference in tension at the top and bottom would be
View SolutionA ball of mass 'm' is rotated in a vertical by a string. The difference in tension at the top and bottom would be
View SolutionA ball of mass M is rotating in a conical pendulum by a string of length L . If radius of circular path is L/sqrt(2) , find the velocity of mass
View SolutionA vertical force of magnitude Facts at the top of a string of mass 'm' and length 'l'. A body of mass M hangs at the bottom of the string.
View SolutionA ball of mass attached to a string of length is released when the string is horizontal. It strikes another ball of mass suspended to another string of length at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
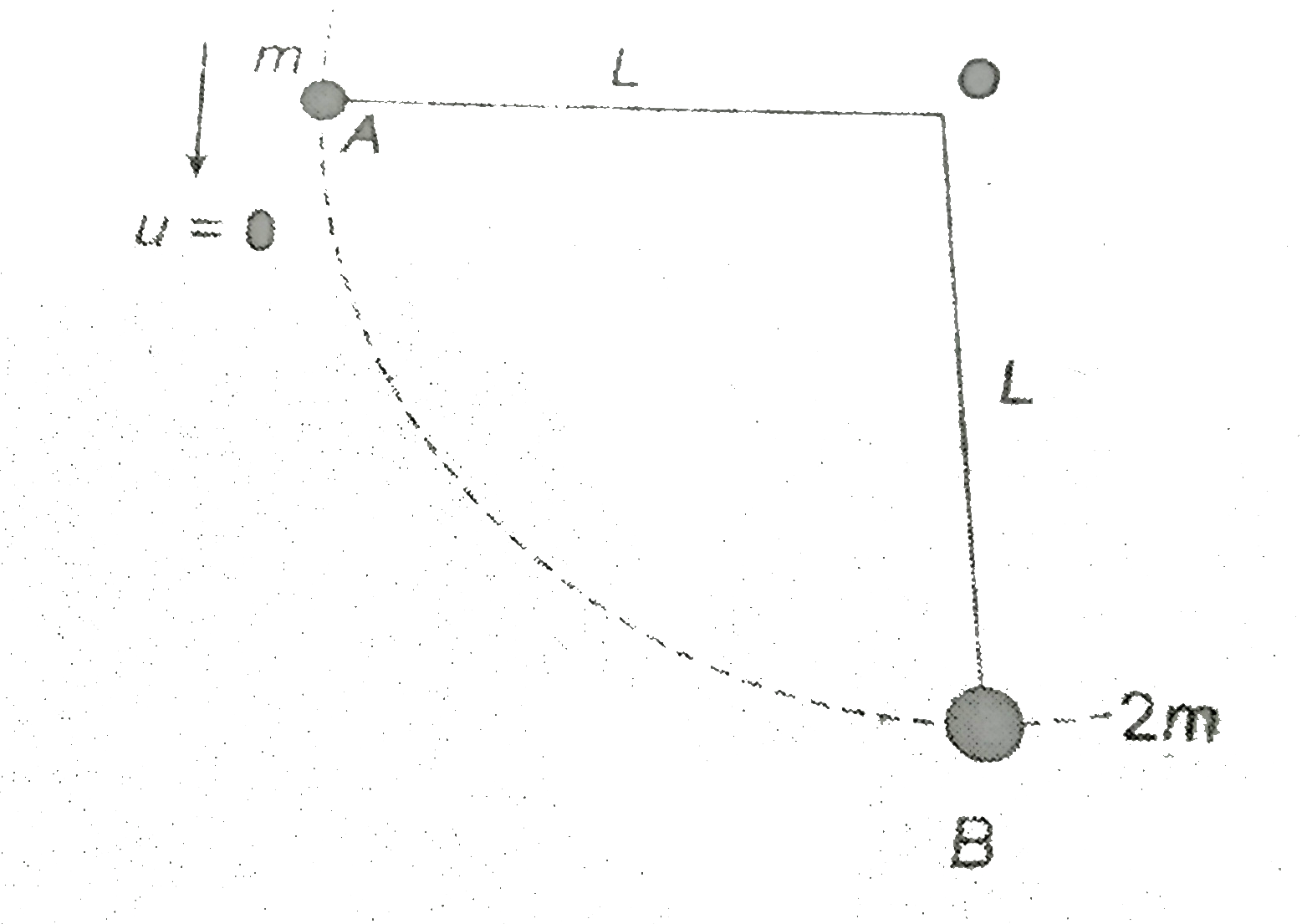
View Solution