A ball of mass m is fastened to a string. The ball swings in a vertical circle of radius R with the other end of the string held fixed. Neglecting the air resistance, the difference between the string's tension at the bottom of the circle and at the quarter of the cirlce is
mg
3mg
4 mg
6 mg
The correct Answer is:B
From energy conservation
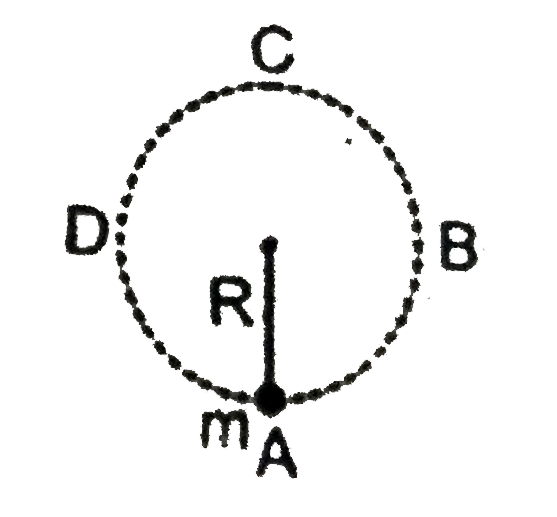
12mV2A=12mV3B+mgR
V2A−V2B=2gR
TA−mg=mV2AR
TB=mV2BR
TA−TB=mg+mR(V2A−V2B)=mg+mR.2gR=3mg
Topper's Solved these Questions
Similar Questions
A particle is fastened at the end of a string adis whirled in a verticle circle with the other end of het string being fixed. The motion of the particle is
View SolutionA small body of mass m is tried to a string and revolved in a vertical circle of radius r. If the tension in the string at the highest point is mg, what is its speed there?
View Solution
Knowledge Check
A body of mass m tied to a string is moved in a vertical circle of radius r. The difference in tensions at the lowest point and the highest point is
A2mgB6mgC4mgD8mgA body of mass m is tied to free end of dtring and whiled in a circle about the other end .If the string suddenly breaks , then
Acentripetal force will vanishBthe body will move along tangent to circleCthe body will move towards or away the centreDboth 'a' and 'b'A stone is fastened to one end of a string and is whirled in a verticla circle of radius R. Find the minimum speed the stone can have at the highest point of the circle.
Av=√3RgBv=√RgCv=√4RgDv=√7Rg
A partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
View SolutionA point mass m is moved in vertical circle of radius r with help of string. Velocity of mass is 7gr√ at lowest point. Tension in string at lowest point is
View SolutionA stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA stone of a mass m tied to a string of length /is rotated in a circle with the other end of the string as the centre. The speed of the stone is V. If the string breaks, the stone will
View SolutionA particle of mass m is rotating by means of a string in a vertical circle. The difference in the tension at the bottom and top would be-
View Solution
