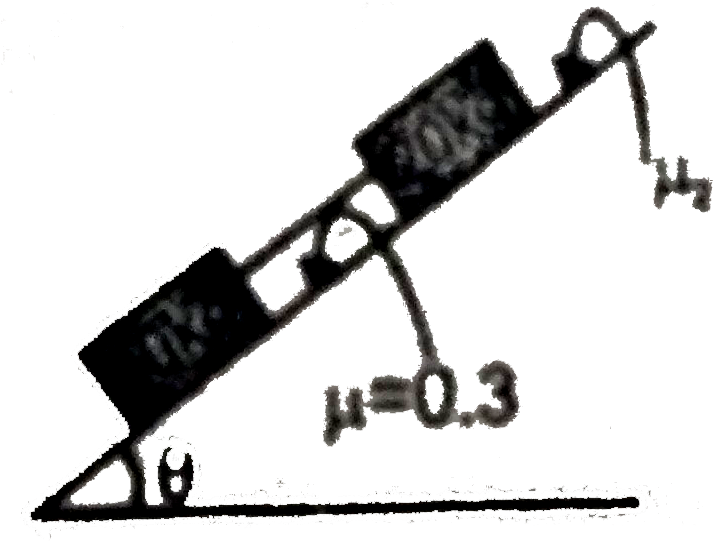
Value of θ is increased gradually from θ=0. At θ=tan−1(12) both the blocks just start slipping. Than value of μ2 is : (g=10m/s2)
A
0.5
B
0.4
C
0.6
D
0.3
Video Solution
Text Solution
The correct Answer is:C
At limiting case (10+20) g sinθ=[(10)(0.3)+20μ2]gcosθ⇒μ2=0.6
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If θ is an acute angle and tanθ+cotθ=2, then the value of tan5θ+cot10θ is:
A1B2C3D4If θ be acute and tanθ+cotθ=2, then the value of tan5θ+cot10θis
A1B2C3D4If cos θ=35 , then the value of sinθ.tanθ+12tan2θ is
A88160B91160C92160D93160
If 2tan−1(cosθ)=tan−1(2cosecθ),(θ≠0) , then find the value of θ.
View SolutionFind the value of θ if
sec2θ+tan2θ=1
View SolutionIf tan2θ.tan4θ=1, then the value of 3θ is
View SolutionIf tan2θ=1, then the general value of θ is
View SolutionIf cosθ=35 , then the value of sinθ−tanθ+12tan2θ is
View Solution

