The switch is closed at t = 0. The time after which the rate of dissipation of energy in the resistor is equal to rate at which energy is being stored in the inductor is:
Related Solutions
The switch is closed at . The time after which the rate of dissipation for energy in the resistor is equal to rate at which energy is being stored in the inductor is : (A) (B) (C) (D)
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionConsider the circuit in Fig. When the switch is closed in position and opens in position , electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio as a function of time.
c. If the time constant of circuit is , what is the time at which ?
View SolutionAn ideal inductor, (having initial current zero) a resistor and an ideal battery are connected in series at time t = 0 . At any time t , the battery supplies energy at the rate P_(B) , the resistor dissipates energy at the rate P_(R ) and the inductor stores enegy at the rate P_(L) .
View Solution5A 50 mH inductor is in series with a 10 2 resistor and a battery with an emf oj 25 V. At t = 0 the switch is closed. Find Q(c) the rate at which energy is stored in the inductor,
View SolutionA Henry inductor coil is connected to a resistance in series as shown in figure. The time at which rate of dissipation of energy (Joule's heat) across resistance is equal to the rate at which magnetic energy is stored in the inductor, is:
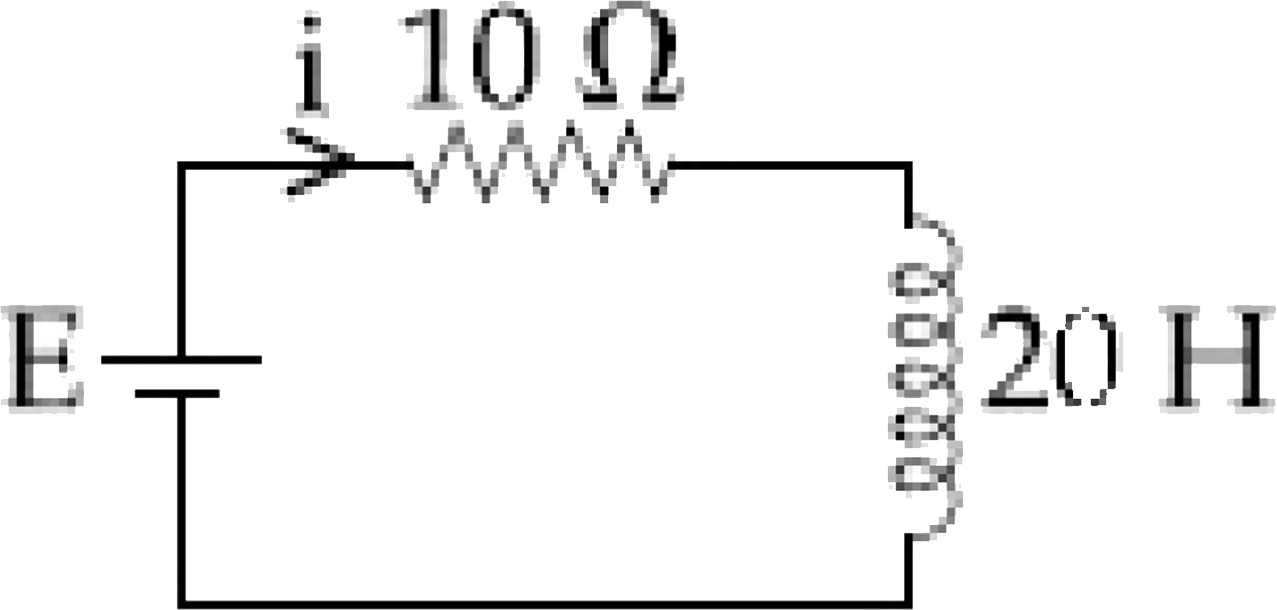
View SolutionAt , switch closed. Find the ratio of the rate at which magnetic energy stored in the coil to the rate at which energy is supplied by the battery at time .
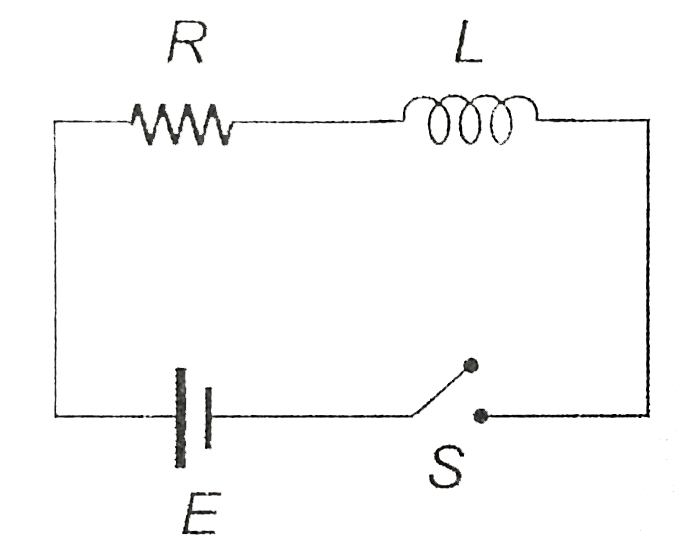
View SolutionIn the given at t = 0 , switch S is closed. The energy stored in the inductor at any instant t (0 lt t oo) will be
View SolutionIn the given at t = 0 , switch S is closed. The energy stored in the inductor at any instant t (0 lt t oo) will be
View SolutionIn the given circuit at , switch S is closed
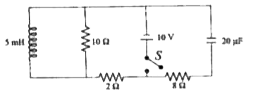
The energy stored in the inductor at any instant will be
View SolutionA resistor and inductor are connected in series through a battery. The switch is closed at time t=0 . Then what is the magnitude of current flowing when rate of increases of magnetic energy in the inductor is maximum
View SolutionIn the given at , switch is closed.
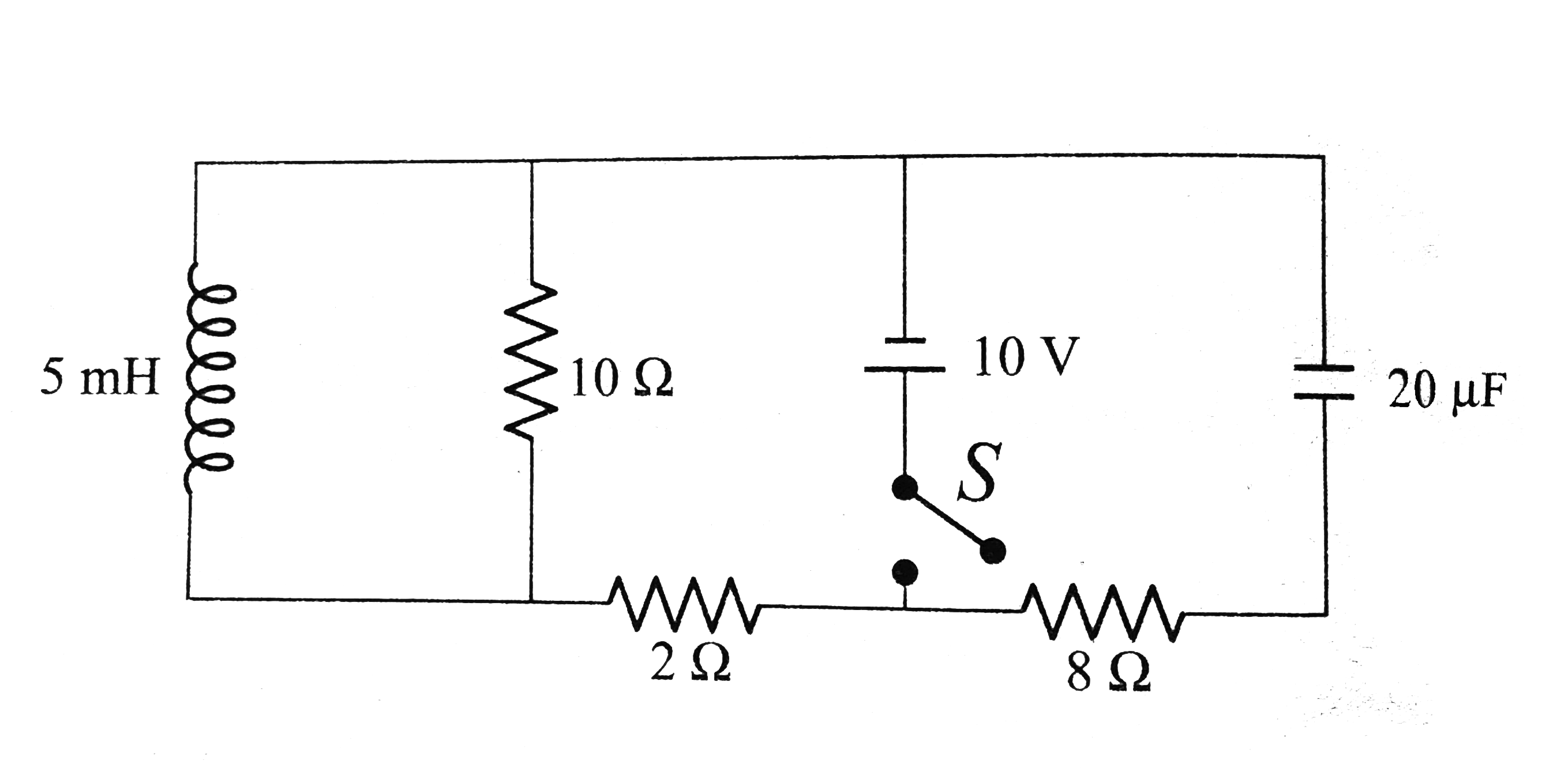
The energy stored in the capacitor and inductor, respectively, at will be
View SolutionIn the given circuit at , switch S is closed

The energy stored in the capacitor and inductor respectively, at will be
View SolutionIn the given at t = 0 , switch S is closed. The energy stored in the capacitor and inductor, respectively, at t rarr oo will be
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
View SolutionThe capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
View SolutionThe capacitor shown in the figure is initially uncharged, the battery is ideal. The switch S is closed at time t = 0, then the time after which the energy stored in the capacitor becomes one-fourth of the energy stored in it in steady state, is:
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View Solution