A long straight wire carries a current i. A particle having a positive charge q and mass m kept at a distance x0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
At minimum separation the x-component of velocity of the particle will be zero. Find the acceleration of the particle due to the magnetic force and solve to get the expression for velocity and displacement.Let the particle be initially at P. Take the wire as the y-axis and the foot of perpendicular from P to the wire as the origin. Take the line OP as the x-axis. We have OP= X0. The magnetic field B at any point to the right of the wire is along the negative z-axis. The magnetic force on the particle is therefore in the x-y plane. As there is no initial velocity along the z-axis the motion will be in the x-y plane. Also its speed remains unchanged. As the magnetic field is not uniform the particle does not go along a circle.Initially x = x0 and vy = 0. At minimum separation from the wire vx = so that vy=-v.
Related Solutions
A long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.

View SolutionA long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.

View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance from the wire is projected towards it with a speed v, as shown in Fig. Find the minimum separation between the wire and the particle.
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
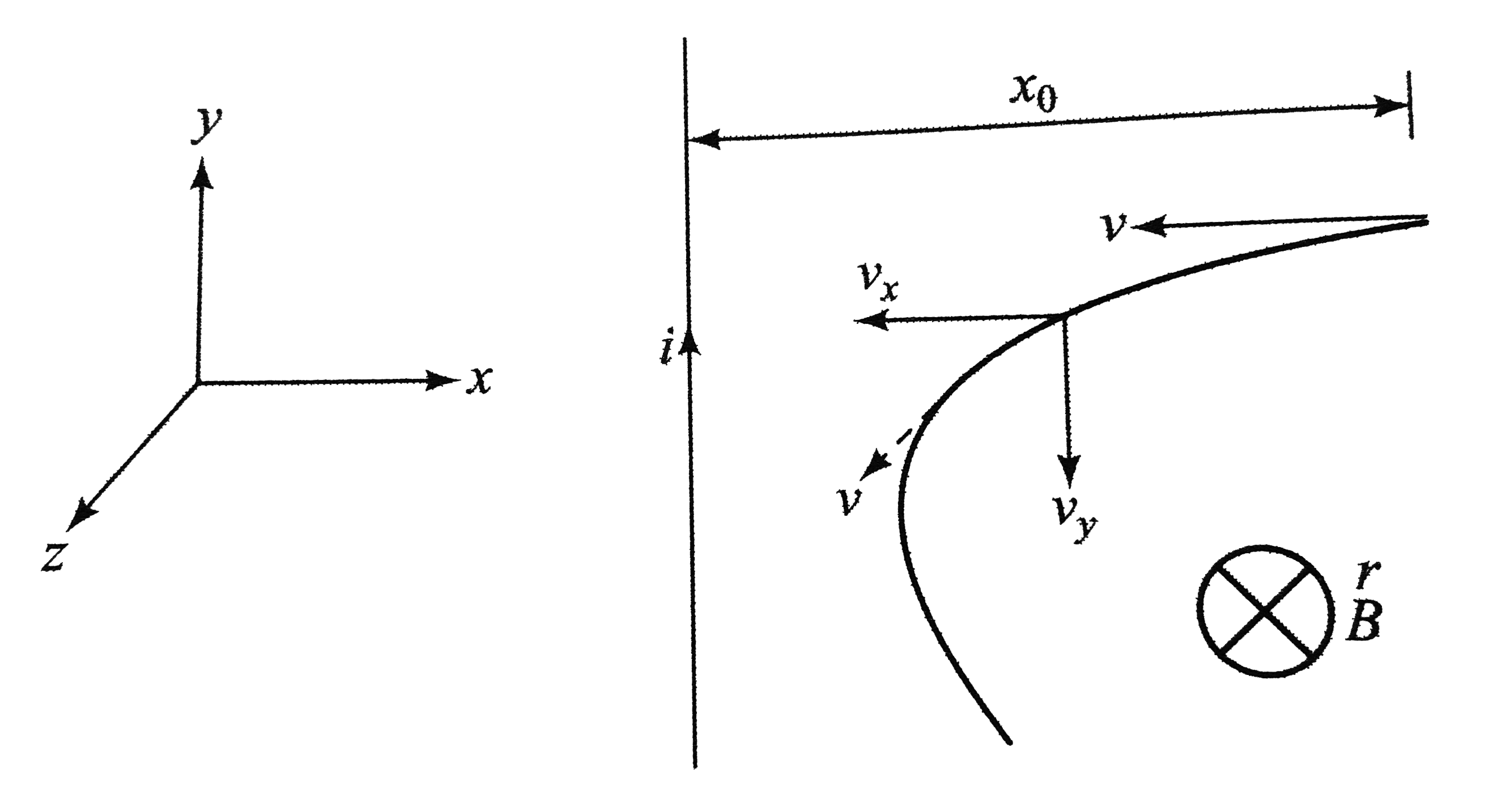

View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x_0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
View SolutionA long straight wire carries a charge with linear density lambda . A particle of mass m and charge q is released at a distance r from the wire. The speed of the particle as it crosses a point at distance 2r from the wire is
View SolutionAn infinitely long current carrying wire carries current i. A particle of mass m and charge q is projected with speed v parallel to the direction of current at a distance r from it. Then, the radius of curvature at the point of projection is:
View SolutionA long straight wire carries a charge with linear density . A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA long straight wire carries a charge with linear density lamda . A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View SolutionA positive point charge q of mass m , kept at a distance x_(0) (in the same plane) from a fixed very long straight current is projected normally away from it with speed v .Find the maximum separation between the wire and the particle.
View SolutionA positive point charge q of mass m , kept at a distance x_(0) (in the same plane) from a fixed very long straight current is projected normally away from it with speed v .Find the maximum separation between the wire and the particle.
View SolutionTwo infinitely long straight current carrying wires are placed parallel to y-axis in xy plane. Each wire carries current I in opposite directions as shown. A charged particle of charge and mass m is project from position P(0,0,0a) with initial velocity v=i. Then
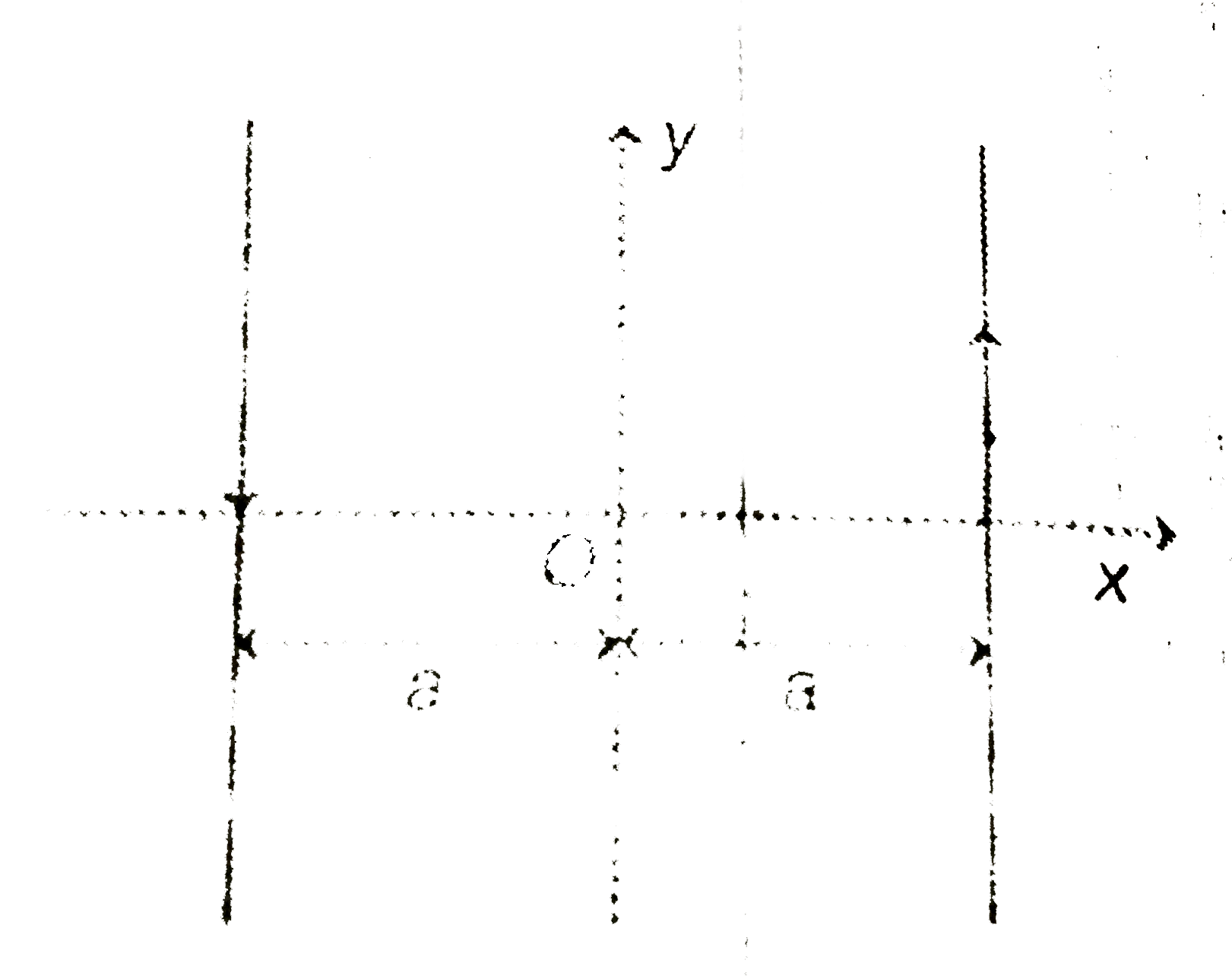
View SolutionTwo infinitely long straight current carrying wires are placed parallel to y-axis in xy plane. Each wire carries current I in opposite directions as shown. A charged particle of charge and mass m is project from position P(0,0,0a) with initial velocity v=i. Then

View SolutionA long straight wire carries a current , a particle having a positive charge and mass is kept at a distance from the axis of the wire is projected away from it with a speed . Find the maximum separation between particle and wire is found to be Find .
View SolutionAn infinitely long current carrying wire carries current i. A charge of mass m and charge q is projected with speed v parallel to the direction of current at a diatance r from it. Then, the radius of curvature at the point of projection is
View SolutionTwo infinite long straight current carrying wires are placed parallel to y-axis in x-y plane. Each wire carries current I in opposite direction as shown. A charged particle of charge +q and mass m is projected from position P (0,0,a) with initial velocity vecv=vechatj . Then
View SolutionA rod of length is kept parallel to a long wire carrying constant current . It is moving away from the wire with a velocity . Find the emf induced in the wire when its distance from the long wire is .
View SolutionA straight wire 5m long is placed parallel to an infinitely long straight wire carrying current 5A. The distance between the two wires is 10 cm and the 5m long wire is carrying current 2A. The force on the shorter wire is :
View SolutionTwo long straight wires, each carrying a current in opposite directions are separated by a distance . The magnetic induction at a point mid way between the wire is
View Solution