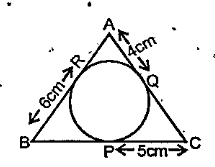
Using the figure given below prove that AR = 1/2 perimeter of triangle ABC
Perimeter of ∆ABC= AB BC CA = AB+[ BP+CP]+CA= AB+BQ+CR+CA Tangents from an external point are equal = AQ+AR= AR+AR Tangents from an external point are equal =2AR
Related Solutions
In the given figure ar . AC is the median of . If ar (ACE) = ?
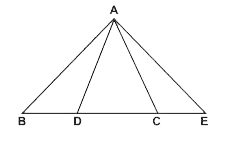
View SolutionIn the given figure, ABC and DBC are two triangles on the same base BC. Prove that .
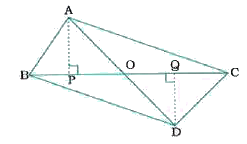
View SolutionIf the medians of a triangle ABC meet at G, prove that ar (AGB) = ar (AGC) = ar (BGC) = (1)/(3) is ar (ABC).
View SolutionThe base BC of Delta ABC is divided at D, so that BD=(1)/(2)DC. Prove that ar(Delta ABD)=(1)/(3)ar(Delta ABC)
View SolutionIn Figure 1, PQ || BC and AP : PB = 1 : 2.find the ratio of
View SolutionGiven if then find
View SolutionIt is given that Delta ABC - Delta PQR , with (BC)/(QR) = (1)/(4) . Then (ar Delta PQR)/(ar Delta ABC) is equal to:
View SolutionIn the given figure,Delta ABC and Delta DBC are on the same base BC.If AD intersects BC at O , prove that (ar(Delta ABC))/(ar(Delta DBC))=(AO)/(DO)
View SolutionIn figure the perimeter of is
View SolutionIt is given that
View SolutionUsing the figure given of prove that
View Solutionand are on the same base BC. Prove that
View SolutionIf D, E, f are the mid-point of the sides of triangle ABC, prove that : .
View Solutionयह दिया है कि के साथ है I तब बराबर है :
View SolutionIn the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta ABE) = ar (DeltaACE)
View SolutionIn the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta BED) = ar (DeltaCDE)
View SolutionIn the figure given below, ABC and DBC are two triangles on the same base BC. If AD intersects BC at , show that .
View SolutionIn the given figure, AD is the median and E is any point on AC, such that ar( Delta MDE) : ar( Delta ABD) = 2 : 3, then find the ratio of ar( Delta EDC): ar( Delta ABC).
View SolutionIn the figure, …………..
View SolutionFind the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View Solution