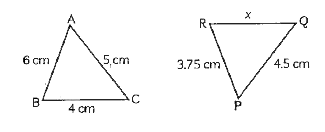
It is given that ΔABC−ΔPQR, with BCQR=14. Then arΔPQRarΔABC is equal to:
16
3
13
19
The correct Answer is:A
To solve the problem, we need to find the ratio of the areas of triangles PQR and ABC given that the triangles are similar and the ratio of the lengths of one pair of corresponding sides is given.
1. Understand the Given Information:
We know that triangles ABC and PQR are similar. The ratio of the lengths of the sides BC and QR is given as:
BCQR=14
2. Use the Property of Similar Triangles:
For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides. Therefore:
arΔPQRarΔABC=(QRBC)2
3. Substitute the Given Ratio:
We know that:
BCQR=14
This implies:
QRBC=4(by taking the reciprocal)
4. Calculate the Area Ratio:
Now, substituting this into the area ratio formula:
arΔPQRarΔABC=(4)2=16
5. Final Answer:
Thus, the ratio of the areas of triangle PQR to triangle ABC is:
arΔPQRarΔABC=16
We know that triangles ABC and PQR are similar. The ratio of the lengths of the sides BC and QR is given as:
BCQR=14
For similar triangles, the ratio of their areas is equal to the square of the ratio of their corresponding sides. Therefore:
arΔPQRarΔABC=(QRBC)2
We know that:
BCQR=14
This implies:
QRBC=4(by taking the reciprocal)
Now, substituting this into the area ratio formula:
arΔPQRarΔABC=(4)2=16
Thus, the ratio of the areas of triangle PQR to triangle ABC is:
arΔPQRarΔABC=16
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - ASSERTION AND REASON BASED MCQs
4 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - CASE - BASED MCQs
15 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
Knowledge Check
It is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
A23B32C49D94If △ABC - △PQR and BCQR = 14 then ar(△PQR)ar(△ABC) =
A14B41C116D161In ΔABCandΔDEF, we have ABDE=BCEF=ACDF=57, then ar(ΔABC):ar(ΔDFR)=?
A5:7B25:49C49:25D125:343
The base BC of ΔABC is divided at D, so that BD=12DC.Prove that ar(ΔABD)=13ar(ΔABC)
View SolutionGiven △ABC~△PQR if ABPQ=13 then find ar△ABCar△PQR
View SolutionIf ΔABC~ΔPQR and 4A(ΔABC)=25A(ΔPQR) then AB : PQ = ?
View SolutionGiven that : ΔABC~ΔPQR , If area (ΔPQR)area (ΔABC)=256441 and PR = 12 cm, then AC is equal to
View SolutionIf PS is median of the triangle PQR, then ar(ΔPQS): ar(ΔQRP) is

View Solution