If PS is median of the triangle PQR, then ar(ΔPQS): ar(ΔQRP) is

1 : 1
2 : 1
1 : 2
Can't be determined
The correct Answer is:C
Step by step video, text & image solution for If PS is median of the triangle PQR, then ar(DeltaPQS): ar(DeltaQRP) is by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE (Match the Following )
Explore 2 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:EXERCISE (Assertion & Reason Type )
Explore 5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBook:MTG IIT JEE FOUNDATIONChapter:AREAS OF PARALLELOGRAMS AND TRIANGLESExercise:NCERT SECTION ( EXERCISE 9.4)
Explore 19 Videos
- CIRCLES Book:MTG IIT JEE FOUNDATIONChapter:CIRCLES Exercise:OLYMPIAD/HOTS CORNER
Explore 6 Videos
Similar Questions
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that ΔABC~ΔPQR.
View SolutionSides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Prove that ΔABC~DetlaPQR
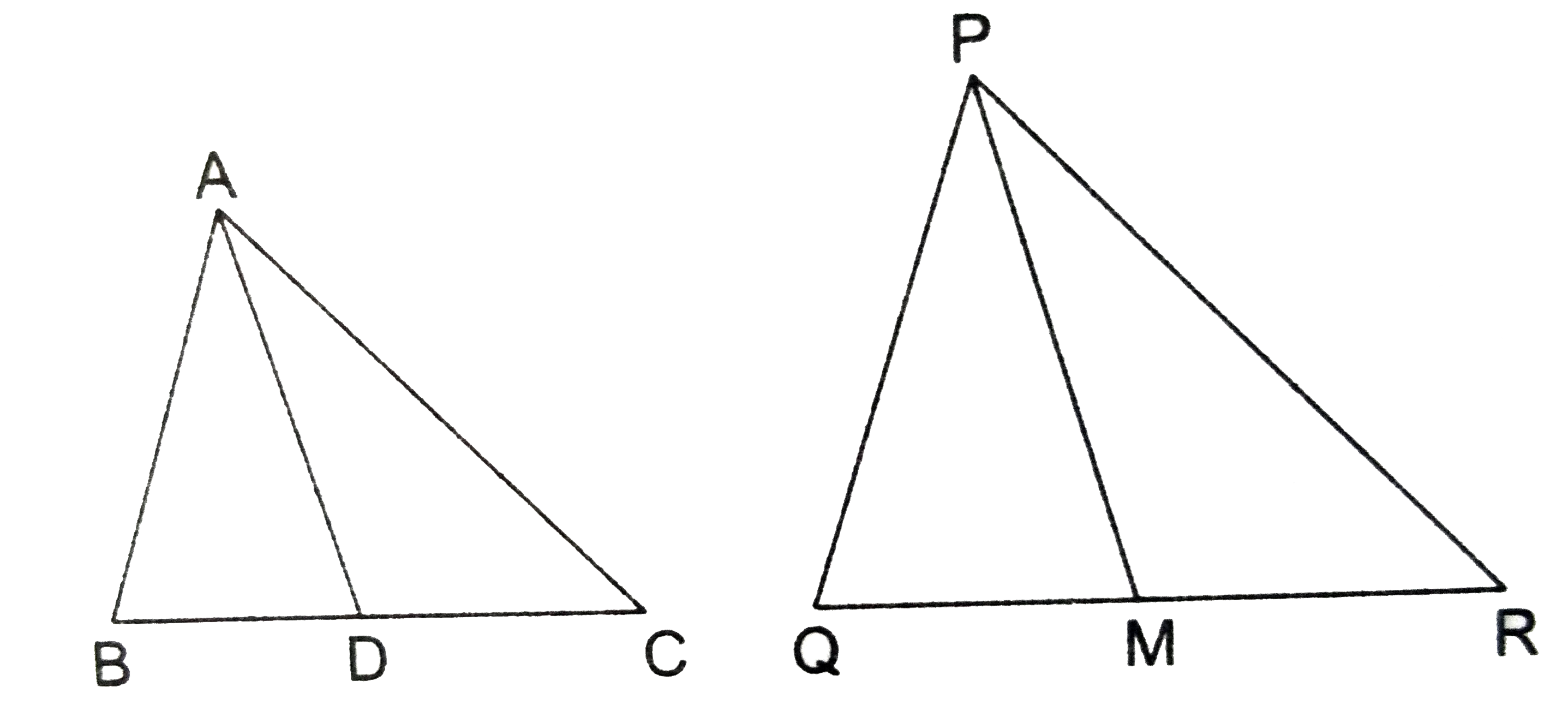
View Solution
Knowledge Check
Assertion : In a parallelogram PQRS, QS is one of the diagonals then ar(ΔPQS) = ar(ΔQRS)
Reason : If a planar region formed by a figure R is made up of two no noverlapping planar regions formed by figures R1 and R2, then ar(R) = ar(R1) + ar(R2).AIf both assertion and reason are tme and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is trne.Triangle ABC is similar to triangle PQR and AB : PQ = 2 : 3. AD is the median to the side BC in triangle ABC and PS is the median to the side QR in triangle PQR. What is the value of (BD/QS)2?
A3/5B4/9C23D4/7triangle ABC is similar to triangle PQR and AB: PQ = 2: 3. AD is the median to the side BC in triangle ABC and PS is the median to the side QR in triangle PQR. What is the value of (BD/QS)2?
A35B49C23D47
D is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionAD and PM are medians of triangles ABC and PQR respectively where ΔABC~ΔPQR. Prove that: ABPQ=ADPM.
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)
View SolutionDiagonal PR and QS of quadrilateral PQRS intersects at T such that PT= TR and PS= QR, show that ar (ΔPTS)= ar (ΔRTQ)
View Solutiontriangle ABC is similar to triangle PQR and AB: PQ = 2: 3. AD is the median to the side BC in triangle ABC and PS is the median to the side QR in triangle PQR. What is the value of (BD/QS)2?
View Solution
