In a square PQRS, X and Y are mid points of sides PS and QR respectively. XY and QS intersect a t O. Find the area of ΔXOS, if PQ = 8 cm.
6 cm2
12 cm2
4 cm2
8 cm2
The correct Answer is:D
To find the area of triangle XOS in square PQRS where PQ = 8 cm, we can follow these steps:
Step 1: Draw the Square
Draw square PQRS with vertices P, Q, R, and S. Since PQ = 8 cm, each side of the square is also 8 cm.
Step 2: Identify Midpoints
Identify the midpoints X and Y of sides PS and QR respectively. Since PS and QR are both 8 cm, the coordinates of the midpoints will be:
- X (midpoint of PS) = (0, 4)
- Y (midpoint of QR) = (8, 4)
Step 3: Determine Coordinates of Vertices
Assign coordinates to the vertices of the square:
- P = (0, 0)
- Q = (8, 0)
- R = (8, 8)
- S = (0, 8)
Step 4: Find the Equation of Line XY
The line segment XY is horizontal at y = 4, as both X and Y have the same y-coordinate. Therefore, the equation of line XY is:
y=4
Step 5: Find the Equation of Line QS
The line segment QS connects points Q and S. The slope of line QS can be calculated as:
slope=8−00−8=−1
Using point-slope form, the equation of line QS is:
y−0=−1(x−8)
Simplifying this gives:
y=−x+8
Step 6: Find the Intersection Point O
To find the intersection point O of lines XY and QS, set their equations equal:
4=−x+8
Solving for x gives:
x=4
Thus, the coordinates of point O are:
O=(4,4)
Step 7: Determine the Area of Triangle XOS
Triangle XOS has vertices at X(0, 4), O(4, 4), and S(0, 8). The base of triangle XOS can be taken as segment XO, which is 4 cm (from (0, 4) to (4, 4)), and the height from point S to line XO, which is 4 cm (from y = 4 to y = 8).
Step 8: Calculate the Area
The area of triangle XOS can be calculated using the formula:
Area=12×base×height
Substituting the values:
Area=12×4×4=162=8cm2
Thus, the area of triangle XOS is 8 cm².
---
Draw square PQRS with vertices P, Q, R, and S. Since PQ = 8 cm, each side of the square is also 8 cm.
Identify the midpoints X and Y of sides PS and QR respectively. Since PS and QR are both 8 cm, the coordinates of the midpoints will be:
- X (midpoint of PS) = (0, 4)
- Y (midpoint of QR) = (8, 4)
Assign coordinates to the vertices of the square:
- P = (0, 0)
- Q = (8, 0)
- R = (8, 8)
- S = (0, 8)
The line segment XY is horizontal at y = 4, as both X and Y have the same y-coordinate. Therefore, the equation of line XY is:
y=4
The line segment QS connects points Q and S. The slope of line QS can be calculated as:
slope=8−00−8=−1
Using point-slope form, the equation of line QS is:
y−0=−1(x−8)
Simplifying this gives:
y=−x+8
To find the intersection point O of lines XY and QS, set their equations equal:
4=−x+8
Solving for x gives:
x=4
Thus, the coordinates of point O are:
O=(4,4)
Triangle XOS has vertices at X(0, 4), O(4, 4), and S(0, 8). The base of triangle XOS can be taken as segment XO, which is 4 cm (from (0, 4) to (4, 4)), and the height from point S to line XO, which is 4 cm (from y = 4 to y = 8).
The area of triangle XOS can be calculated using the formula:
Area=12×base×height
Substituting the values:
Area=12×4×4=162=8cm2
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )
2 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Assertion & Reason Type )
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19 Videos
- CIRCLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6 Videos
Similar Questions
In the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
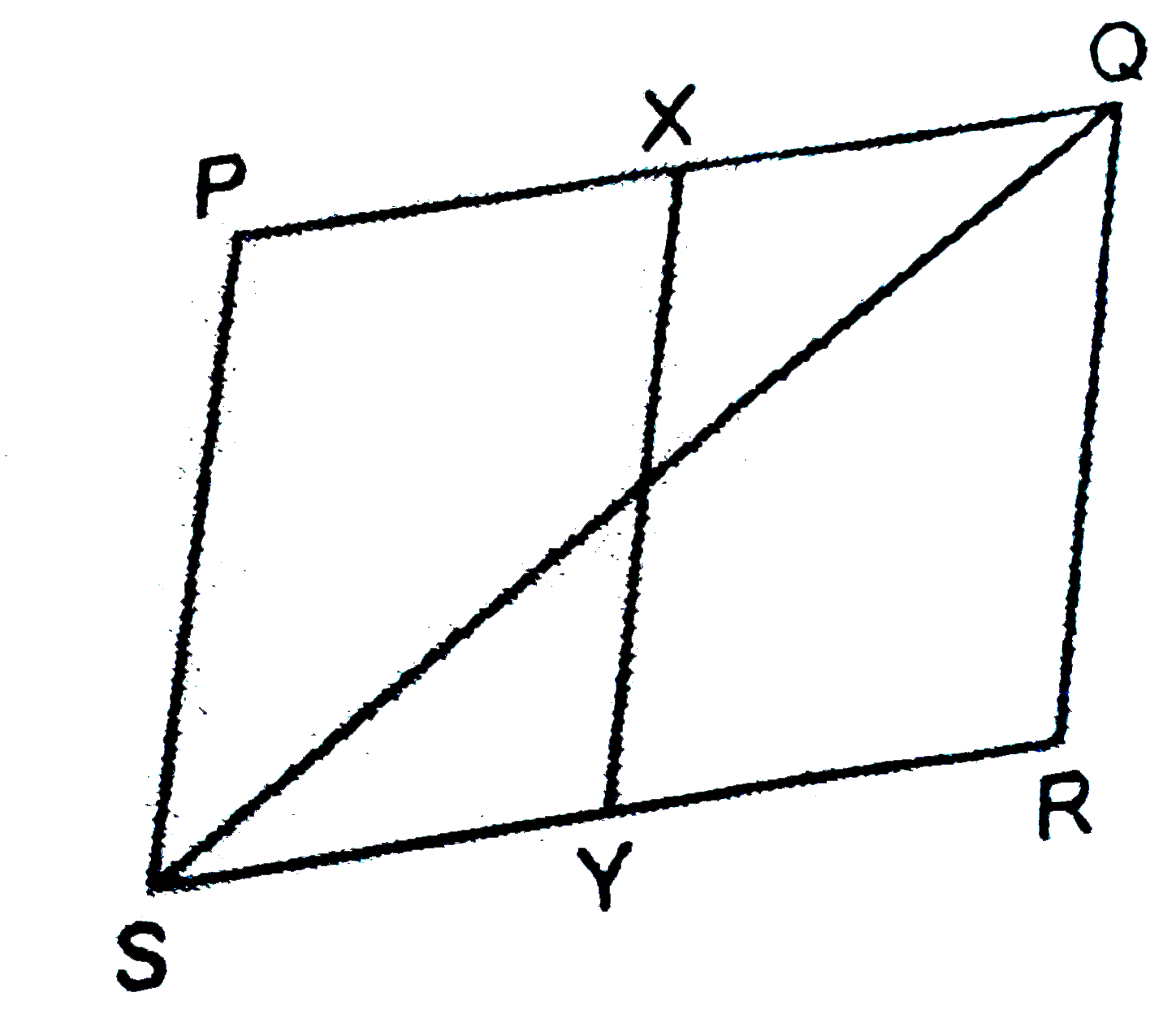
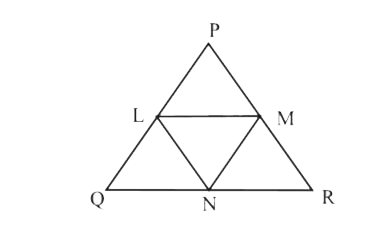
View SolutionIn the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View Solution
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3PQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
A24B6C16D12
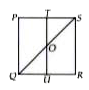
In the given figure, PQRS is a square and T and U are respectively, the mid-points of PS and QR. Then what is the area of ∆OTS if PQ = 8 cm?
View SolutionPQR is a triangle right-angled at Q. If X and Y are the mid-points of the sides PQ and QR respectively, then which one of the following is not correct?
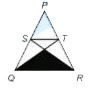
View SolutionIn the given figure , PQR is an equilateral triangle with side as 12 cm . S and T are the mid points of the sides PQ and PR respectively . What ist he area (in cm2) of the shaded region ?
View SolutionPQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
View SolutionLet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
View Solution
