In the following figure, AB II CD. Diagonals AC and BD intersect at point O. If BO : OD = 1 : 3, then (area of $Δ$ AOB)/(area of $Δ$ ABD) =

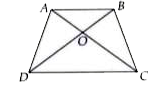
1/4

1/9

116

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Answer

Step by step video, text & image solution for In the following figure, AB II CD. Diagonals AC and BD intersect at point O. If BO : OD = 1 : 3, then (area of DeltaAOB)/(area of DeltaABD) = by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Match the Following )
2videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE (Assertion & Reason Type )
5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - NCERT SECTION ( EXERCISE 9.4)
19videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CIRCLES EXERCISE - OLYMPIAD/HOTS CORNER
6videos
CIRCLES

Knowledge Check

Question 1 - Select One
In a trapezium ABCD, the diagonals AC and BD interserted other at O such that $O B : O D = 3 : 1$ then the ratio of area of $Δ A O B : Δ C O D$ is :
A $3 : 1$
B $1 : 4$
C $9 : 1$
Dcan't be determined

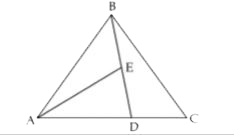
In the given figure ABC is a triangle in which 3AD = CD and E lies on BD, DE = 2BE. What is the ratio of area of $Δ A B C$ and area of $Δ A B E$ ?

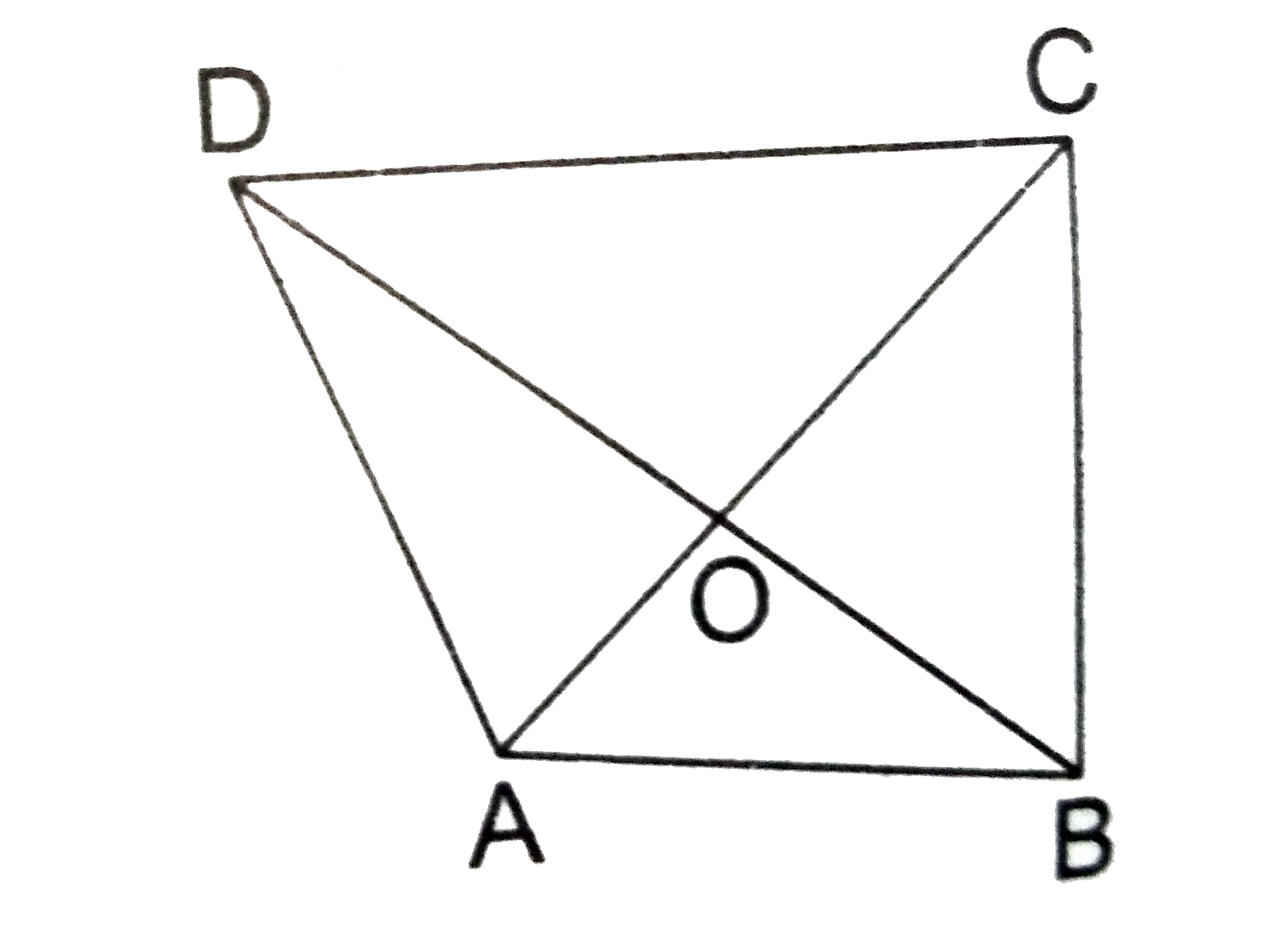
View Solution
In the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If $B O = O D$ , prove that
$a r (△ A B C) = a r (△ A D C)$ .

View Solution
ABC is a triangle median CD and BE intersects at point O then find the ratio of area $(Δ O D E) : (Δ A B C)$ .
View Solution
In the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar( $Δ$ DOC) = ar( $Δ$ AOB)
View Solution
In the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar( $Δ$ DCB) = ar( $Δ$ ACB)
View Solution
In the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) $A B + B C + C D + D A < 2 (A C + B D)$
(b) $A B + B C + C D + D A > (A C + B D)$

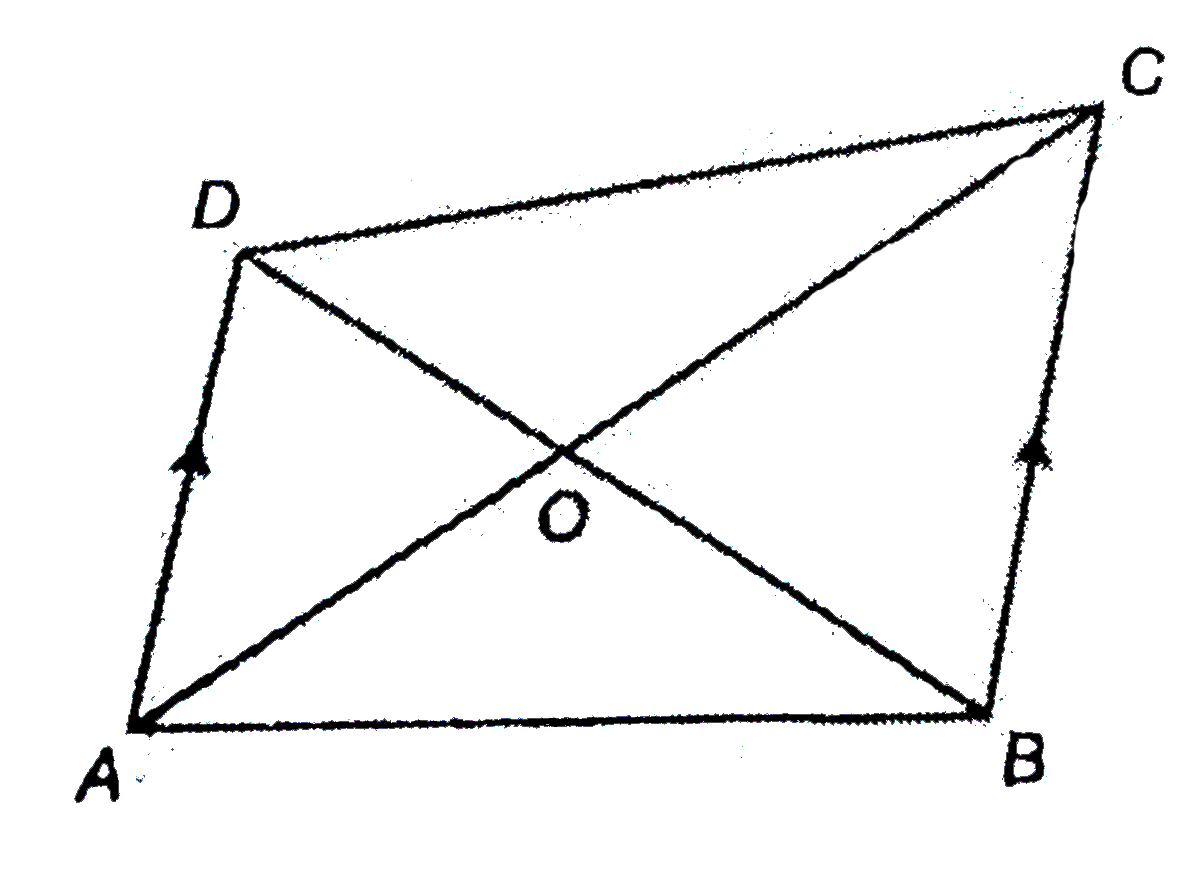
View Solution
In the adjoining figure, ABCD is a quadrilateral in which $A D ∣ ∣ B C$ . AC and BD intersect each other at point 'O'. Prove that:
area of $Δ C O D = area of Δ A B O$

View Solution

MTG IIT JEE FOUNDATION-AREAS OF PARALLELOGRAMS AND TRIANGLES-EXERCISE ( Multiple Choice Questions )

In a trapezium ABCD, AB || DC, AB = a cm, and DC = b cm. If M and N ar...
02:16
In a class, teacher gave two cardboard pieces having equal area which ...
01:59
In the figure, ABCD is a square. E and Fare midpoints of AD and BC res...
03:03
In the given figure, PQRS is parallelogram, then find the area of Delt...
Text Solution
If the area, base and corresponding altitude of a parallelogram are x^...
Text Solution
In the given figure, AD is the median and E is any point on AC, such t...
Text Solution
The figure formed by joining the midpoints of the adjacent sides of a ...
04:39
PQRS is a rhombus in which angleR = 60°. Then PR : QS =
Text Solution
The lengths of the diagonals of a rhombus are 12 cm and 16 cm. The are...
Text Solution
In a quadrilateral ABCD, it is given that BD = 16 cm. If AL bot BD and...
Text Solution
In. the figure the angles BAD and ADC are right angles and AE I I BC, ...
03:47
ABCD is a parallelogram in which BC is produced to E such that CE = BC...
06:01
A swimming pool, 30 m long has a depth of water of 80 cm at one end an...
02:25
In a square PQRS, X and Y are mid points of sides PS and QR respective...
05:54
In figure, if ar(DeltaABC) = 28 cm^(2), then find ar( I I^(gm) AEDF).
02:53
Which of the following statements is false?
Text Solution
The medians of Delta ABC intersect at point G. Prove that: area of D...
03:59
The perimeter of an isosceles right triangle is 2p, its area is
06:53
In the figure, the semicirce centered at O has a diam.eter 6 cm. The c...
03:04
In the following figure, AB II CD. Diagonals AC and BD intersect at po...
02:28

Home
Ask Doubt
Profile

In the following figure, AB II CD. Diagonals AC and BD intersect at point O. If BO : OD = 1 : 3, then (area of ΔAOB)/(area of ΔABD) =

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a trapezium ABCD, the diagonals AC and BD interserted other at O such that OB:OD=3:1 then the ratio of area of ΔAOB:ΔCOD is :

MTG IIT JEE FOUNDATION-AREAS OF PARALLELOGRAMS AND TRIANGLES-EXERCISE ( Multiple Choice Questions )

In the following figure, AB II CD. Diagonals AC and BD intersect at point O. If BO : OD = 1 : 3, then (area of $Δ$ AOB)/(area of $Δ$ ABD) =

In a trapezium ABCD, the diagonals AC and BD interserted other at O such that $O B : O D = 3 : 1$ then the ratio of area of $Δ A O B : Δ C O D$ is :