PQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
24
6
16
12
The correct Answer is:A
To solve the problem, we need to find the area of triangle BCD given that the area of triangle PQR is 48 cm².
1. Understanding the Rectangle and Triangles:
- PQRS is a rectangle.
- A, B, C, and D are the midpoints of sides PQ, QR, RS, and PS respectively.
2. Area of Triangle PQR:
- The area of triangle PQR is given as 48 cm².
3. Identifying the Relationship:
- Since A, B, C, and D are midpoints, triangles PAB, QBC, RCD, and SDA are formed within the rectangle.
- Triangle BCD is formed by connecting the midpoints of the sides of triangle PQR.
4. Area of Triangle BCD:
- Triangle BCD is similar to triangle PQR, and its area can be derived from the area of triangle PQR.
- The area of triangle BCD is one-fourth of the area of triangle PQR because the midpoints divide the triangle into smaller triangles of equal area.
5. Calculating the Area:
- Area of triangle BCD = (1/4) * Area of triangle PQR
- Area of triangle BCD = (1/4) * 48 cm²
- Area of triangle BCD = 12 cm².
Final Answer:
The area of triangle BCD is 12 cm².
- PQRS is a rectangle.
- A, B, C, and D are the midpoints of sides PQ, QR, RS, and PS respectively.
- The area of triangle PQR is given as 48 cm².
- Since A, B, C, and D are midpoints, triangles PAB, QBC, RCD, and SDA are formed within the rectangle.
- Triangle BCD is formed by connecting the midpoints of the sides of triangle PQR.
- Triangle BCD is similar to triangle PQR, and its area can be derived from the area of triangle PQR.
- The area of triangle BCD is one-fourth of the area of triangle PQR because the midpoints divide the triangle into smaller triangles of equal area.
- Area of triangle BCD = (1/4) * Area of triangle PQR
- Area of triangle BCD = (1/4) * 48 cm²
- Area of triangle BCD = 12 cm².
The area of triangle BCD is 12 cm².
Similar Questions
PQR is a triangle right-angled at Q. If X and Y are the mid-points of the sides PQ and QR respectively, then which one of the following is not correct?
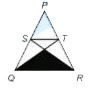
View SolutionIn the given figure , PQR is an equilateral triangle with side as 12 cm . S and T are the mid points of the sides PQ and PR respectively . What ist he area (in cm2) of the shaded region ?
View Solution
Knowledge Check
PQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
A24B6C16D12PQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
A10√2cmB20√2cmC25√2cmD15√2cmLet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM
PQRS is a rectangle. The ratio of the sides PQ and QR is 3:1. If the length of the diagonal PR is 10cm, then what is the area (in cm2) of the rectangle?
View SolutionPQR is a triangle such that PQ = PR. RS and QT are the median to the sides PQ and PR respectively. If the medians RS and QT intersect at right angle, then what is the value of (PQ/QR)2?
View SolutionPQR is a triangle, whose area is 180 cm2. S is a point on side QR, such that PS is the angle bisector of ∠QPR. If PQ: PR = 2: 3, then what is the area (in cm2) triangle PSR?
View SolutionPQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
View SolutionPQR is a triangle, whose are is 180cm2 . S is a point on side QR, such that PS is the angle bisector of ∠QPR . If PQ : PR = 2 : 3 , then what is the area (in cm2) triangle PSR ?
View Solution