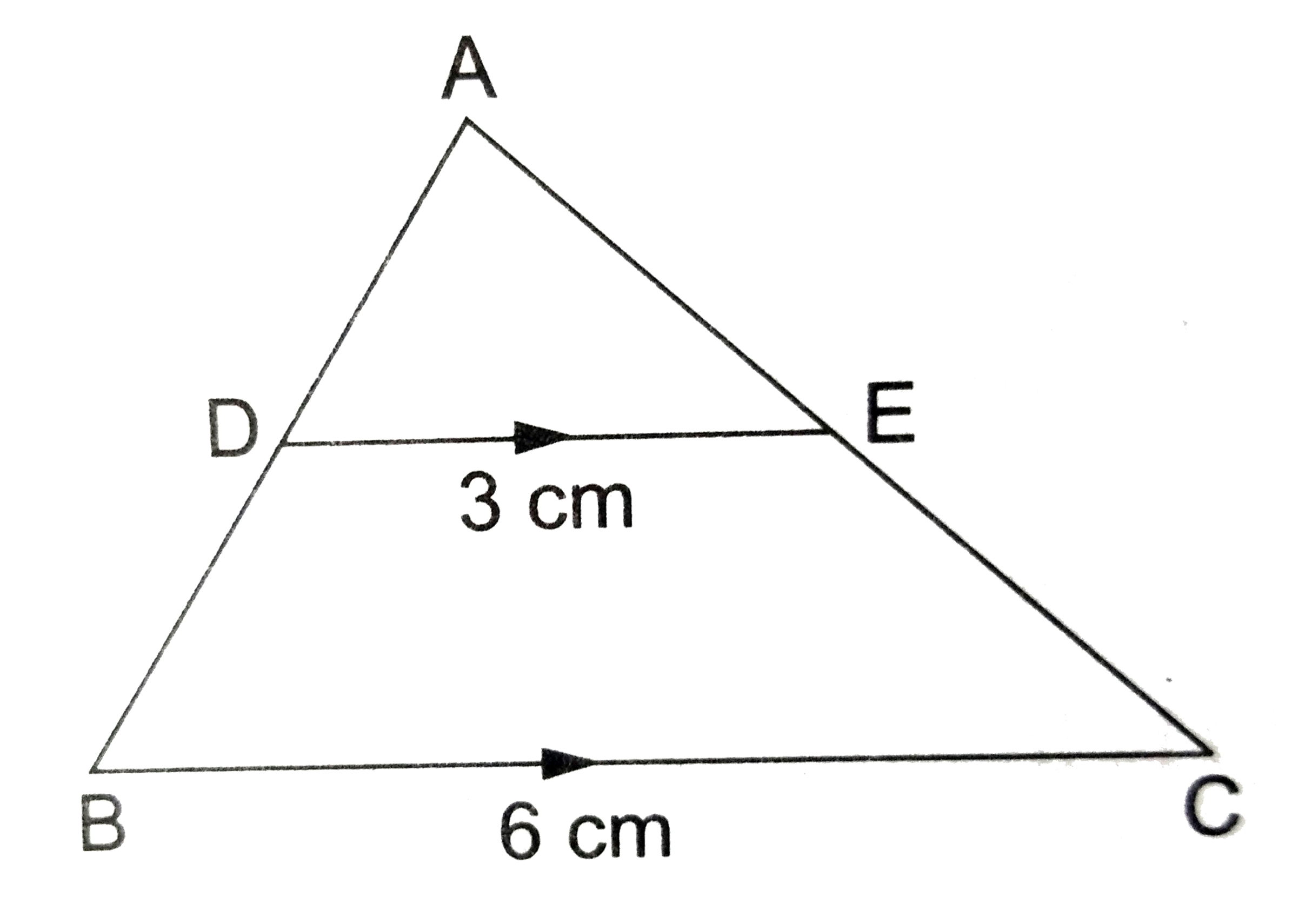
In the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
14cm2
7cm2
21cm2
28cm2
The correct Answer is:B
Step by step video, text & image solution for In the given figure ar (Delta ABC)=" ar "(Delta ADE). AC is the median of Delta ADE. If ar (ACE) =14 cm^(2)" then ar "(Delta ABC) = ? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PART-A (Fill in blanks :)
18 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Part-B
5 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE TEST
3 Videos
Similar Questions
Knowledge Check
In a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
A10B12C14D√221
In given figure. If area of parallelogram ABCD is 30cm2 then find ar (ΔADE)+ ar (ΔBCE)
View SolutionIn the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
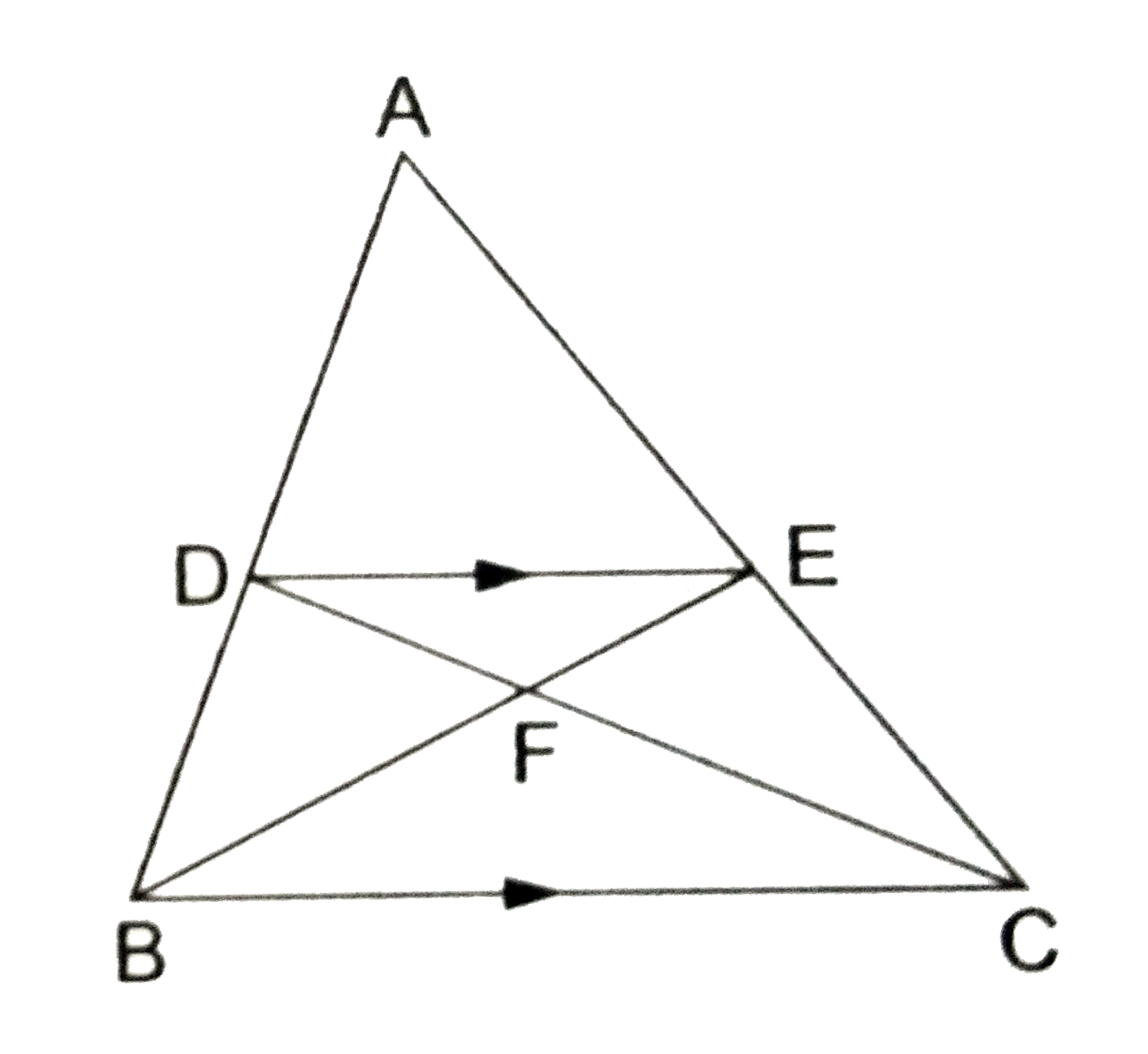
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
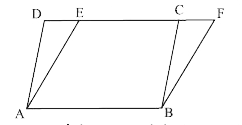
View SolutionIn the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
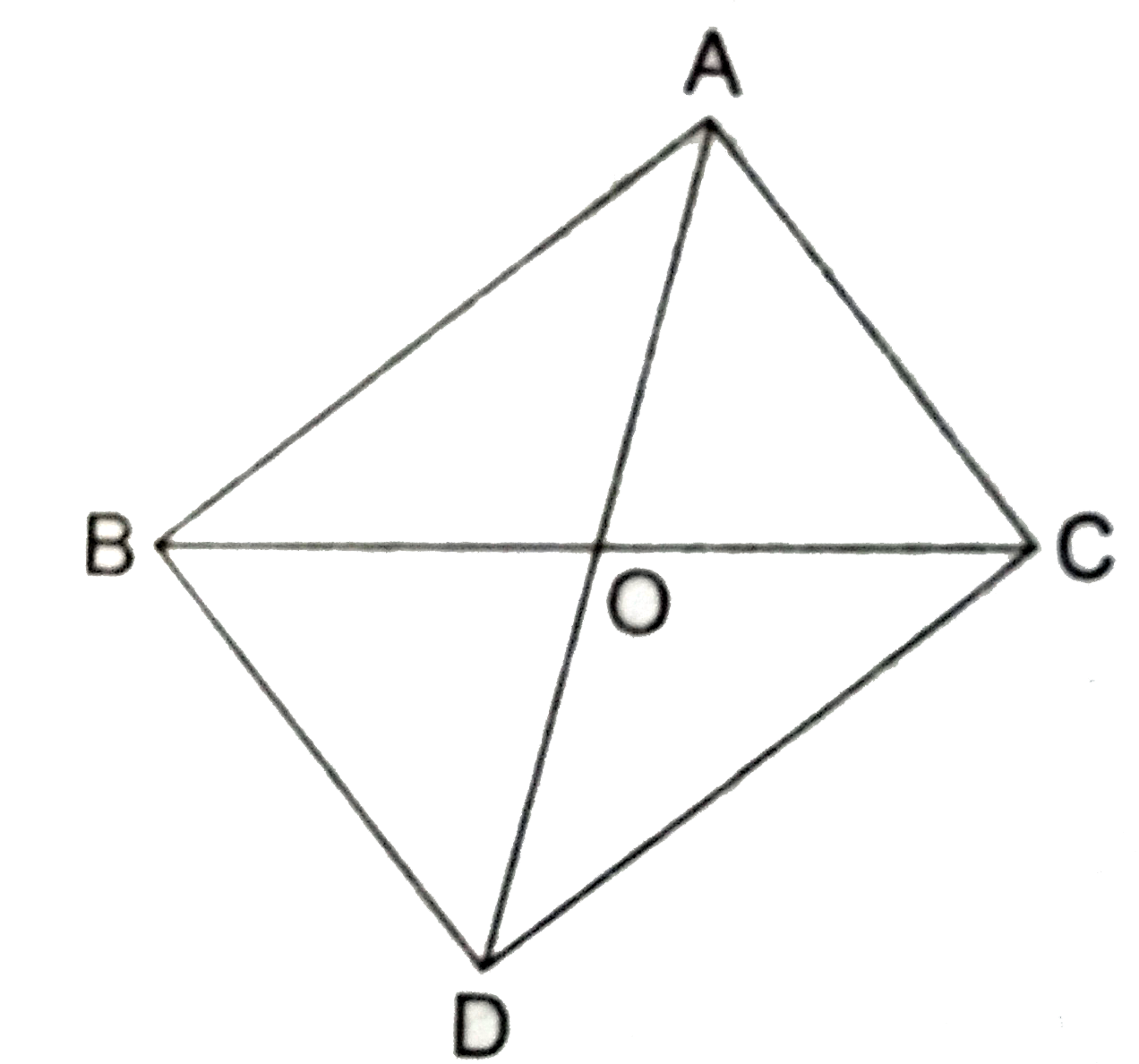
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View Solution