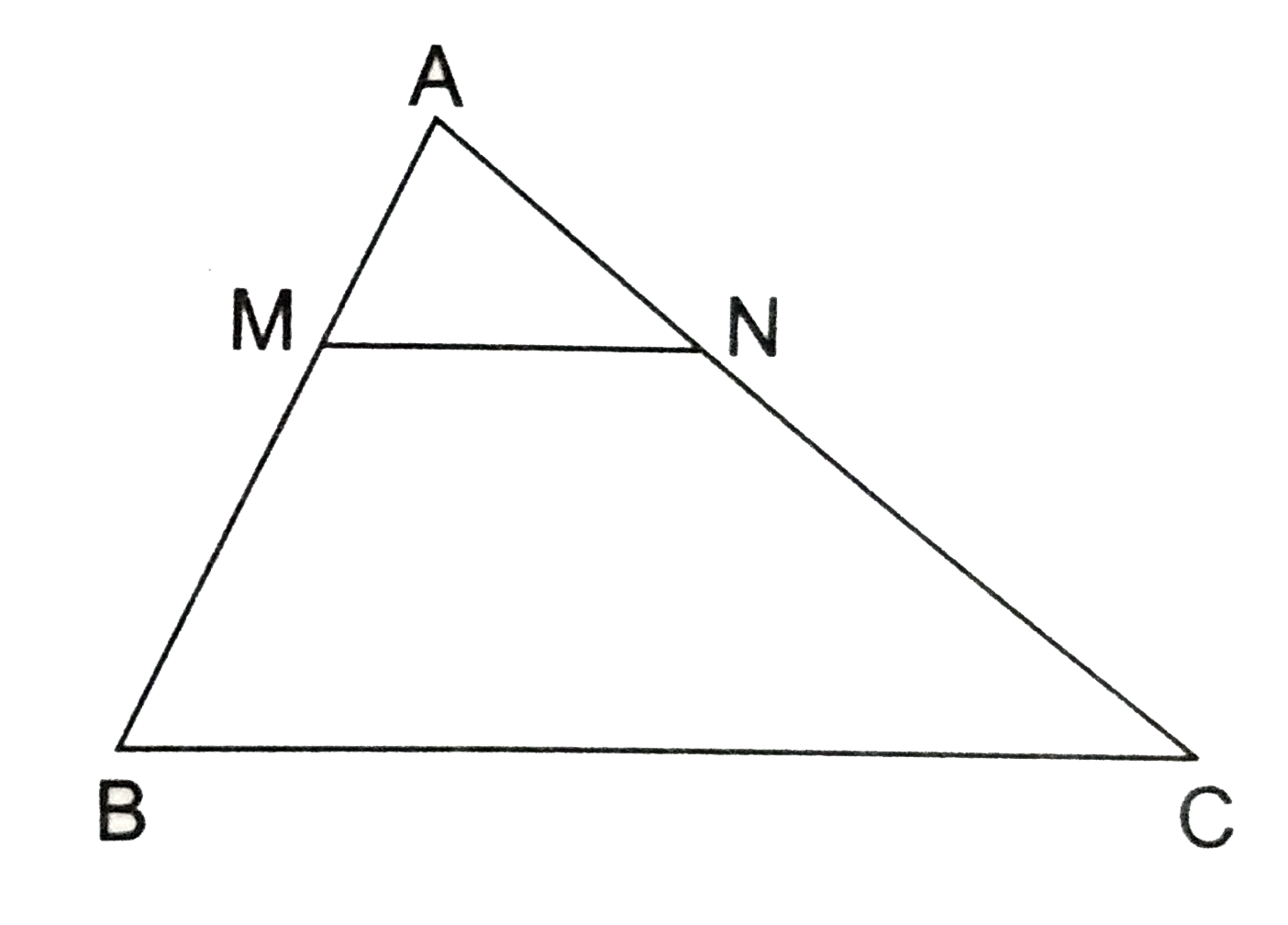
In the figure, MN∣∣BC and AM:MB=1:3, then ar(△AMN)ar(△ABC)=…………..
The correct Answer is:116
Step by step video, text & image solution for In the figure, MN |\| BC " and " AM : MB = 1 : 3, " then " (ar(triangle AMN))/(ar(triangle ABC)) = ………….. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:VERY SHORT QUESTIONS
Explore 10 Videos
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:SHORT ANSWER (SA-I) TYPE QUESTIONS
Explore 30 Videos
- TRIANGLESBook:EDUCART PUBLICATIONChapter:TRIANGLESExercise:LONG ANSWER TYPE QUESTIONS
Explore 10 Videos
- SURFACE AREAS AND VOLUMESBook:EDUCART PUBLICATIONChapter:SURFACE AREAS AND VOLUMESExercise:LONG ANSWER TYPE QUESTIONS
Explore 30 Videos
Similar Questions
Knowledge Check
If △ABC - △PQR and BCQR = 14 then ar(△PQR)ar(△ABC) =
A14B41C116D161
In △ABC, AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(△APB):ar(△ABC) is equal to :
त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(△APB):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn (ΔABC) , MN∣∣BC and AM:AB=13. Then find the ratio of ar(ΔAMN)ar(ΔABC)
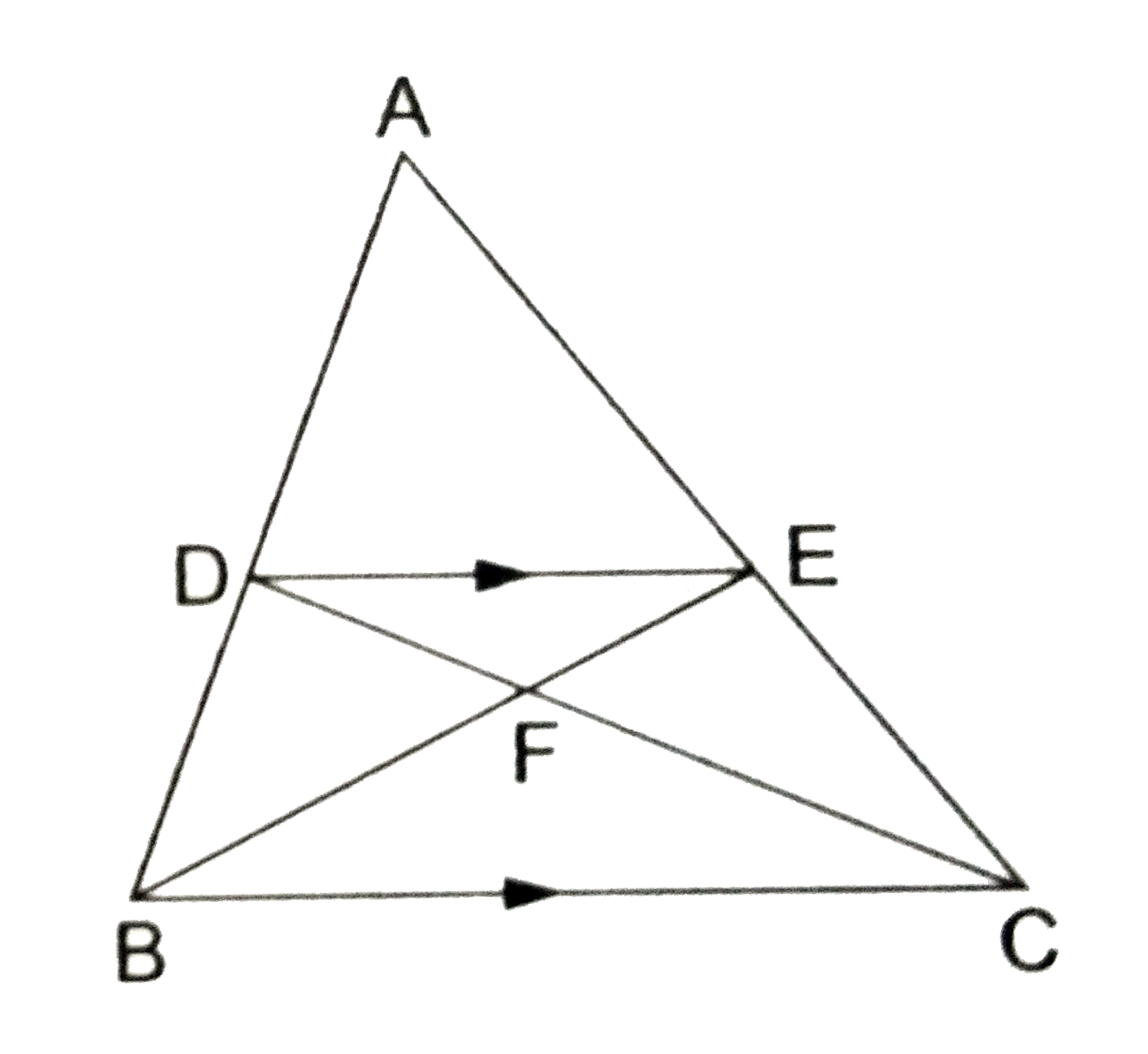
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
View SolutionIn △ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar(△BPD):ar(△ABC) is equal to:
त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar(△BPD):ar(△ABC) ज्ञात करें |
View SolutionIn △ABC, AD is median and G is the point on AD such that AG: GD = 2: 1, then ar(△ABG):ar(△ABC) is equal to :
त्रिभुज ABC में, AD मध्यिका है तथा G, AD पर स्थित ऐसा बिंदु है कि AG: GD = 2 : 1 है, तो ar(△ABG):ar(△ABC) का मान किसके बराबर होगा ?
View SolutionIn the adjoining figure, △ABCand△DBC are on the same base BC with A and D on opposite sides of BC such that ar(△ABC)=ar(△DBC). Show that BC bisect AD.
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
View Solution