A weightless rod of length l with a small load of mass m at the end is hinged at point A Fig. 20 and occupies a strictly vertical position touching a body of mass M. A light jerk sets the system in motion.For what mass ratio M/m will the rod form an angle α = pi/6 with the horizontal at the moment of the separation from the body? What will be the Velocity u of the body at this moment? Friction should be neglected.
As long as the load touches the body the velocity of the latter is equal to the horizontal component of the velocity of the load and the acceleration of the body is equal to the horizontal component of the acceleration of the load.Let a be the total acceleration of the load. Then we can write a = at + ac where ac is the centripetal acceleration of the load moving in the circle of radius l i.e. ac = v2/l where v is the velocity of the load Fig. 154. The horizontal component of the acceleration isThe body also has the same acceleration. We can write the equation of motion for the body:where N is the force of normal pressure exertedby the load on the body. At the moment of separation of the load N = 0 and The acceleration component at at the moment of separation of the load is only due to the force of gravity:Thus the velocity of the load at the moment of separation isand the velocity of the body at the same moment isAccording to the energy conservation law we haveSubstituting the obtained expression for v at the moment of separation and the value of sin α = sin pi/6 = 1/2 into this equation we obtain the ratio:The velocity of the body at the moment of separation is
Related Solutions
A weightless rod of length l with a small load of mass m at the end is hinged at point A (Fig.) and occupies a strictly vertical position, touching a body of mass M. A light jerk sets the system in motion . For what mass ratio M//m will the rod form an angle alpha = pi//6 with the horizontal at the moment of the separation from the body ? What will be the velocity u of the body at this moment ? Friction should be neglected.
View SolutionA weightless rod of length l with a small load of mass m at the end is hinged at point A as shown and occupies a strictly vertical position, touching a body of mass M . A light jerk sets the system in motion. a. For what mass ratio M//m will the rod form an angle alpha=pi//6 with the horizontal at the moment of the separation from the body? b. What will he the velocity u of the body at this moment? Friction should be neglected.
View SolutionA weightless rod of length with a small load of mass at the end is hinged at point as shown and occupies a strictly vertical position, touching a body of mass . A light jerk sets the system in motion.
a. For what mass ratio will the rod form an angle with the horizontal at the moment of the separation from the body?
b. What will he the velocity of the body at this moment? Friction should be neglected.
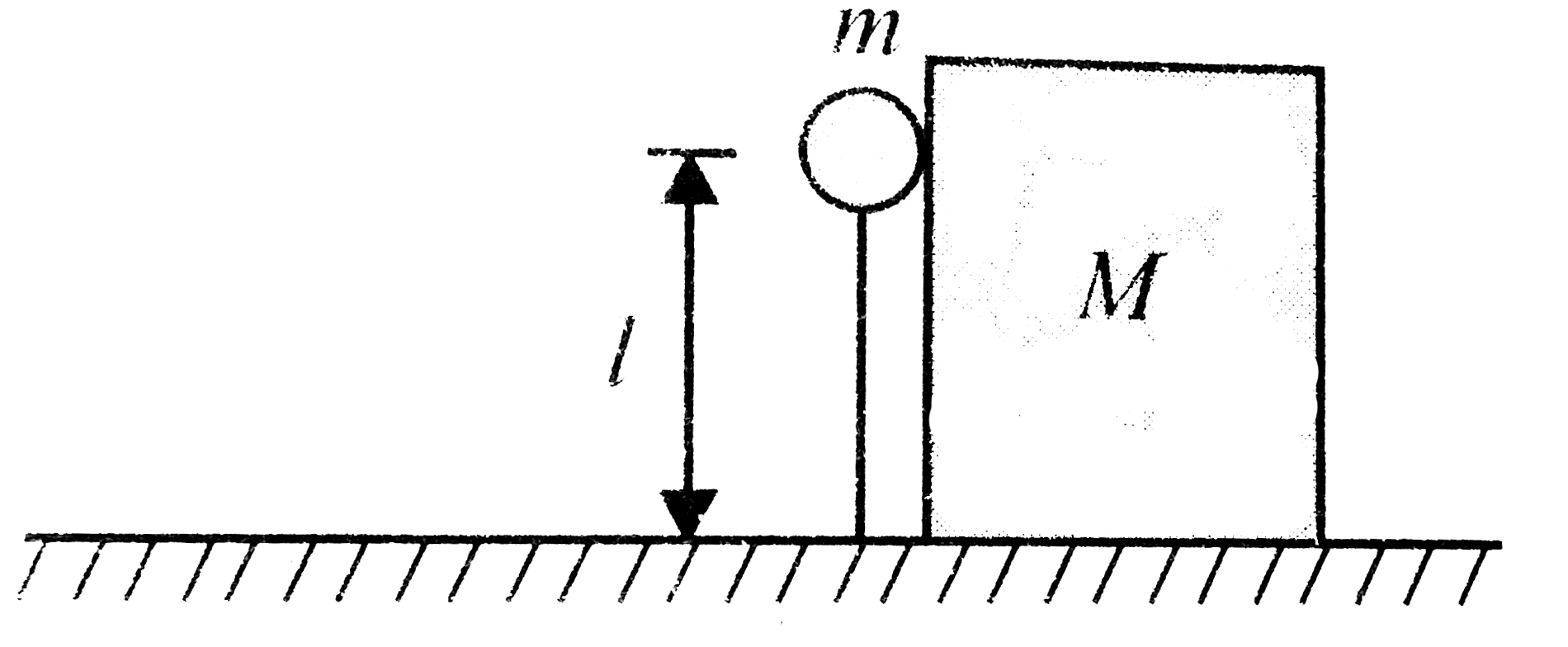
View SolutionA weightless rod of length l with a small load of mass m at one of its end is held vertical with its lower end hinged on a horizontal surface. The load touches a wedge of mass M in this position. A slight jerk towards right sets the system in motion (see figure), with rod rotating freely in vertical plane about its lower end. There is no friction. (a) For what mass ratio M/m will the rod form an angle theta=pi//3 with the vertical at the moment the load separates from the wedge? (b) What is speed of the wedge at that moment? Neglect friction.
View Solutionm और 2m द्रव्यमान के दो कण एक भारहीन छड़ के सिरों पर लगे हुए हैं । छड़ के परितः इस निकाय का जड़त्व - आघूर्ण कितना होगा ?
View SolutionA uniform thin rod of length and mass is hinged at a distance from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l//4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionL लम्बाई तथा M द्रव्यमान की एक छड़ के बिंदु O पर कब्जा लगा है। एक छोटी m द्रव्यमान की गोली चित्रानुसार छड़ पर दागी जाती है गोली छड़ के भीतर धंस जाती है। टकराने के ठीक बार निकाय का कोणीय वेग ज्ञात कीजिए।
View SolutionA thin uniform rod of mass M and length L is hinged at end released from rest in the horizontal position. The tention at a point located at a distance L/3 from the hinge point, when the rod becomes vertical, will be
View SolutionA mass m is connected to a massless rod of length l( and is free to rotate in vertical plane about hinged end of rod. If rod is released from horizontal position and mass "m" collides inelastically at lowest position with identical mass m, as shown in the figure, then the maximum height attained by combined mass will be
View SolutionA uniform thin rod of length and mass is hinged at a distance from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA uniform rod of length and mass 2 m rests on a smooth horizontal table. A point mass moving horizontally at right angles to the rod with velocity collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionFind the frequency of small oscillations of thin uniform vertical rod of mass m and length l hinged at the point O.

View Solutionl लम्बाई की एक भारहीन छड़ पर दो समान द्रव्यमान m चित्रनुसार लगाए गए हैं ,छड़ बिंदु C के पारित : ऊर्ध्वाधर तल मे घूर्णन कर सकती है। छड़ के सिरे A पर कितना क्षैतिज वेग दिया जाना चाइए की यह क्षैतिज दिशा मे मुड़ जाए ?

View SolutionA small bead of mass M is launched from the end of a horizontal rod at a speed u along rod having same mass M. The rod is free to rotate in a vertical plane about a end. Simultaneously the rod is given a angular velocity omega as shown in the figure. Find the angular acceleration of the rod. [The rod is hinged at an end]
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
View Solution