Complete Solutions to PROBLEM of chapter MOTION IN A STRAIGHT LINE of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | MOTION IN A STRAIGHT LINE |
| AAKASH SERIES | PROBLEM |
| Number Of Questions | 59 |
| Academic Year | 2023-24 |
A particle is at x =+ 5 m at t =0,x =- 7 m at t = 6 s and x = + 2 at t = 10s. Find the average velocity of the particle during the intervals
(a)t=0 to t=6s
(b)t=6s to 6=10s
(c ) t=0 to t=10s .
View SolutionA particle traversed half of the distance with a velocity of `V_0`. The remaining parts of the distance was covered with velocity `V_1` for half of the time and with `V_2` for other half of the time. Find the mean velocity of the particle averaged and the whole time of motion
View SolutionTwo parallel rail tracks run north-south. Train A moves north with a speed of `54 km h^(-1)`, and train B moves south with a speed of `90 km h^(-1)`. What is the
(a) velocity of B with respect to A ?,
(b) velocity of ground with respect to B ?, and
(c) velocity of a monkey running on the roof of the train A against its motion (with a velocity of `18 km h^(-1)` with respect to the train A) as observed by a man standing on the ground ?
View SolutionThe displacement x of a particle at the instant when its velocity v is given by `v = sqrt(3x +16)`. Find its acceleration and initial velocity
View SolutionIf `S_n`=2+0.4n find initial velocity and acceleration
View SolutionA body starts from rest and moves with uniform acceleration of `5 ms^(-2)` for 8 seconds. From that time the acceleration ceases. Find the distance covered in 12s starting from rest.
View SolutionThe two ends of a train moving with uniform acceleration pass a certain point with velocity u and v. Find the velocity with which the middle point of the train passes the same point.
View SolutionA scooter can produce a maximum acceleration of `5m s^(-2)`. Its brakes can produce a maximum retardation of `10 "ms"^(-2)`. The minimum time in which it can cover a distance of 1.5 km is ?
View SolutionThe speed of a train is reduced from 60 km/h, to 15 km/h, while it travels a distance of 450 m. If the retardation is uniform, find how much further it will travel before coming to rest ?
View SolutionA rifle bullet loses 1/20th of its velocity in passing through a plank. What will be the least number of such planks required to just stop the bullet ?
View SolutionA body covers 100 cm in first 2 seconds and 128 cm in the next four seconds moving with constant acceleration. Find the velocity of the body at the end of 8 sec ?
View SolutionA car is moving with a velocity of 20 m/s. The driver sees a stationary truck ahead at a distance of 100 m. After some reaction time `Deltat` the brakes are applied producing a retardation of `4 m//s^2`? What is the maximum reaction time to avoid collision ?
View SolutionA car starting from rest, accelerates at the rate of f through a distance S, then continues at constant speed for time t and declerates at the rate f/2 to come to rest. If the total distance travelled is 15 S then S =
View SolutionA driver can stop his car from the red signal at a distance of 20 m when he is driving at 36 kmph and 41.25 m when he is driving at 54 kmph. Find his reaction time.
View SolutionA car starts from rest and moves with uniform acceleration 'a', At the same instant from the same point a bike crosses with a uniform velocity 'u'. When and where will they meet ? What is the velocity of car with respect to the bike at the time of meeting?
View SolutionTwo bodies start moving in the same straight line at the same instant of time from the same origin. The first body moves with a constant velocity of 40 m/s, and the second starts from rest with a constant acceleration of `4 "m/s"^2`. Find the time that elapses before the second catches the first body. Find also the greatest distance between then prior to it and the time at which this occurs.
View SolutionTwo trains one travelling at 54 kmph and the other at 72 kmph are headed towards one an other along a straight track. When they are `1/2` km apart, both drivers simultaneously see the other train and apply their brakes. If each train is decelerated at the rate of `1 ms^(-2)` , will there be collision ?
View SolutionIn a car race, car A takes time t less than car B and passes the finishing point with a velocity v more than the velocity with which car B passes the point. Assuming that the cars start from rest and travel with constant accelerations `a_1` and `a_2` show that `v/t=sqrt(a_1a_2)` .
View SolutionA particle moving along a straight line with initial velocity u and acceleration a continues its motion for n seconds. What is the distance covered by it in the last `n^(th)` second ?
View SolutionA bus accelerates from rest at a constant rate `alpha` for some time, after which it decelerates at a constant rate `beta` to come to rest. If the total time elapsed is t seconds then, evaluate.
(a)the maximum velocity achieved and (b)the total distance travelled graphically.
View SolutionFigure shows the motion of a particle along a straight line. Find the average velocity of the particle during the intervals
(a)A to E , (b) B to E, (c ) C to E , (d) D to E , (e) C to D .
View SolutionVelocity-time graph for the motion of a certain body is shown in Fig. Explain the nature of this motion. Find the initial velocity and acceleration and write the equation for the variation of displacement with time. What happens to the moving body at point B? How does the body move after this moment ?
View SolutionThe graphs in (i) and (ii) show the S-t graph and V -t graph of a body. Are the motions shown in the graphs represented by OAB the same ?
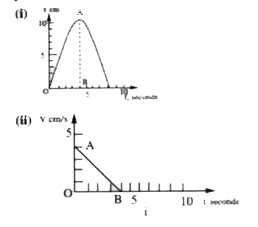
View SolutionA body starts from rest and travels a distance S with uniform acceleration, then moves uniformly a distance 2S and finally comes to rest after moving further 5S under uniform retardation. Find the ratio of average velocity to maximum velocity :
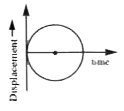
View SolutionFigure given here shows the displacement time graph for a particle. Is it practically possible ? Explain.
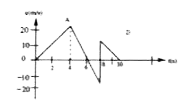
View SolutionFigure given here shows the variation of velocity of a particle with time.
Find the following:
(i) Displacement during the time intervals.
(a) 0 to 2 sec., (b) 2 to 4 sec. and (c) 4 to 7 sec
(ii) Accelerations at
(a)t = 1 sec, (b) t = 3 sec. and (c)t = 6 sec.
(iii) Average acceleration
(a) between t = 0 to t = 4 sec.
(b) between t = 0 to t = 7 sec.
(iv) Average velocity during the motion.
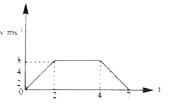
View SolutionThe velocity-time graph of a body moving in a straight line is shown in Fig. Find the displacement and distance travelled by the body in 10 sec.
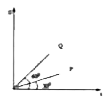
View SolutionThe displacement-time graphs of two particles P and Q are as shown in the figure. The ratio of their velocities `V_P` and `V_Q` will be
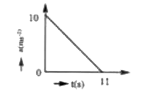
View SolutionThe a -t graph is shown in the figure. The maximum velocity attained by the body from rest will be
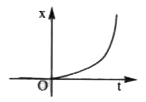
View SolutionFigure shows the x-t plot of one dimensional motion of a particle. Is it correct to say from the graph that the particle moves in a straight line for t `lt` 0 and on a parabolic path for t `gt` 0 ? If not, suggest a suitable physical context for this graph.
View SolutionA car travels starting form rest with constant acceleration `alpha` and reaches a maximum velocity V. It travels with maximum velocity for some time and retards uniformly at the rate of `beta` and comes to rest. If s is the total distance and t is the total time of journey then t=
View SolutionThe motion of a particle along a straight line is described by the function `s = 6 + 4t^2 - t^4` in SI units. Find the velocity, acceleration, at t = 2s, and the average velocity during `3^(rd)` second.
View SolutionA particle moves according to the equation `t= sqrtx +3`, where will be the particle come to the rest for the first time
View SolutionThe velocity of a particle moving in the positive direction of the X-axis varies as `V = KsqrtS` where K is a positive constant. Draw V-t graph.
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as `alpha=ksqrtv`, where k is a positive constant. At the initial moment the velocity of the point is equal to `V_0`. What distance will it take to cover that distance?
View SolutionA body is projected vertically up with velocity u from a tower. It reaches the ground with velocity nu. The height of the tower is `H=u^2/(2g)(n^2-1)`
View SolutionTwo bodies begin to fall freely from the same height. The second body begins to fall `'tau'` s after the first. After what time from the beginning of first body dose the distance between the bodies equals to l?
View SolutionFor a freely falling body, Find the ratio of the times taken to fall successive equal distances.
View SolutionIf a freely falling body covers half of its total distance in the last second of its journey, Find its time of fall.
View SolutionA balloon starts from rest, moves vertically upwards with an acceleration `g/8 "ms"^(-2)`. A stone falls from the balloon after 8s from the start. Find the time taken by the stone to reach the ground `(g=9.8 ms^(-2))`
View SolutionA rocket is fired upwards vertically with a net acceleration of `4"m/s"^2` and initial velocity zero. After 5 seconds its fuel is finished and it decelerates with g. At the highest point its velocity becomes zero. There after it accelerates downwards with acceleration g and return back to ground.
(i) Plot velocity – time graph for complete journey
(ii) Displacement-time graph for the complete journey. (Take `g = 10 m//s^2`.)
View SolutionA ball is thrown upward with an ini tial velocity of `100 "ms"^(-1)`. After how much time will it return ? Draw velocity - time graph for the ball and find from the graph (i) the maximum height attained by the ball and (ii) height of the ball after 15 s. Take `g=10 ms^(-2)` .
View SolutionA stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity `100 ms^(-1)` . Find when and where the two stones meet ?
View SolutionA ball A is dropped from the top of a building and at the same time an identical ball B is thrown vertically upward from the ground. When the balls collide the speed of A is twice that of B. At what fraction of the height of the building did the collison occur?
View SolutionAn object falls from a bridge which is 45 m above the water. It falls directly into a small row - boat moving with constant velocity that was 12m from the point of impact when the object was released. What was the speed of the boat ?
View SolutionTwo balls are dropped to the ground from different heights. One ball is dropped 2s after the other, but both strike the ground at the same time 5s after the Ist is dropped.
(a) What is the difference in the heights from which they were dropped ?
(b) From what height was the first ball dropped?
View SolutionDrops of water fall at regular intervals from the roof of a building of height 16 m. The first drop strikes the ground at the same moment as the fifth drop leaves the roof. Find the distances between successive drops.
View SolutionIf an object reaches a maximum vertical height of 23.0 m when thrown vertically upward on earth how high would it travel on the moon where the acceleration due to gravity is about one sixth that on the earth ? Assume that initial velocity is the same.
View SolutionAn elevator ascends an upward acceleration of 0.2 m/s2. At the instant it upwards speed in 3m/sec a loose bolt 5 m high form the floor drops from the ceiling of the elevator.Find the time until the bolt strikes the floor and the displacement it has fallen .
View SolutionA body falls freely from a height of 125m `(g = 10 m//s^2)` after 2 sec gravity ceases to act Find the time taken by it to reach the ground?
View SolutionA parachutist drops freely from an aeroplane for 10 seconds before the parachute opens out.Then he descends with a net retardation of `2m//sec^(2)`.
His velocity whe he reaches the ground is 8m/sec.Find the height at which he get out of the aeroplane?
View SolutionA stone is dropped into a well and the sound of splash is heard after 5.3 sec. If the water is at a depth of 122.5 m from the ground, the velocity of sound in air is
View SolutionA body is thrown vertically up with a velocity of 100 m/s and another one is thrown 4 sec after the first one. How long after the first one is thrown will they meet?
View SolutionA ball is thrown vertically upward with a velocity 'u' from the balloon descending with velocity v. After what time, the ball will pass by the balloon ?
View SolutionA ball dropped from the 9th story of a multi - storeyed building reaches the ground in 3 second. In the first second of its free fall, it passes through storeys, where n is equal to ( Take `g=10 m s^(-2)`)
View SolutionA stone is dropped into water from a bridge 44.1 m above the water. Another stone is thrown vertically downward 1 s later. Both strike the water simultaneously. What was the initial speed of the second stone?
View SolutionA ball is dropped from the top of a building .It takes 0.5 s to fall past the 3m length of a window some distance from the top of the building .If the velocity of the ball at the top and at the bottom of the window are `V_(T)` and `V_(B)` respectively then `V_(T)+V_(B)=?`
View SolutionA ball is thrown vertically upwards with a velocity of `20 ms^(-1)` from the top of a multistorey building. The height of the point from where the ball is thrown is 25.0 m from the ground. (a) How high will the ball rise ? and (b) how long will it be before the ball hits the ground ? Take `g = 10 ms^(-2)`.
View SolutionA balloon starts from rest from the ground and moves with uniform acceleration g/8. When it reaches a height h a ball is dropped from it. Find the time taken by the ball to reach the ground.
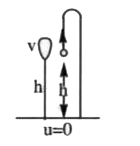
View Solution
PROBLEM questions and complete solutions for chapter MOTION IN A STRAIGHT LINE of JEE (MAIN AND ADVANCED) PHYSICS of Class 12