The motion of a particle along a straight line is described by the function s=6+4t2−t4 in SI units. Find the velocity, acceleration, at t = 2s, and the average velocity during 3rd second. Solution in Telugu
s=6+4t2−t4
Velocity =dsdt=8t−4t3 when t=2
Velocity =8×2−4×23
Velocity =-16 m/s
Acceleration a=d2sdt2=8−12t2 when t=2
acc=8−12×22=-40
acc=−40m/s2
displacement in 2 seconds
s1=6+4.22−24=6 m
displacement in 3 seconds
s2=6+4.32−34=-39 m
displacement during 3rd second
=s2−s1=−39−6=−45 m
∴ Average velocity during 3rd second
=±451=−45 m/s
-ve sign indicates that the body is moving in opposite direction to the initial direction of motion.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
45 Videos
Similar Questions
The ratio of the numerical values of the average velocity and average speed of a body is always
View SolutionA person travels along a straight road for half the distance with velocity V1 and the remaining half distance with velocity V2 the average velocity is given by
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View SolutionThe velocity function of an object moving along a straight line is given by v(t)=At^(2)+Bt . If at t=2s, the velocity is 3 m/s and acceleration is 0.500 m//s^(2) , find the value of the constant A.
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
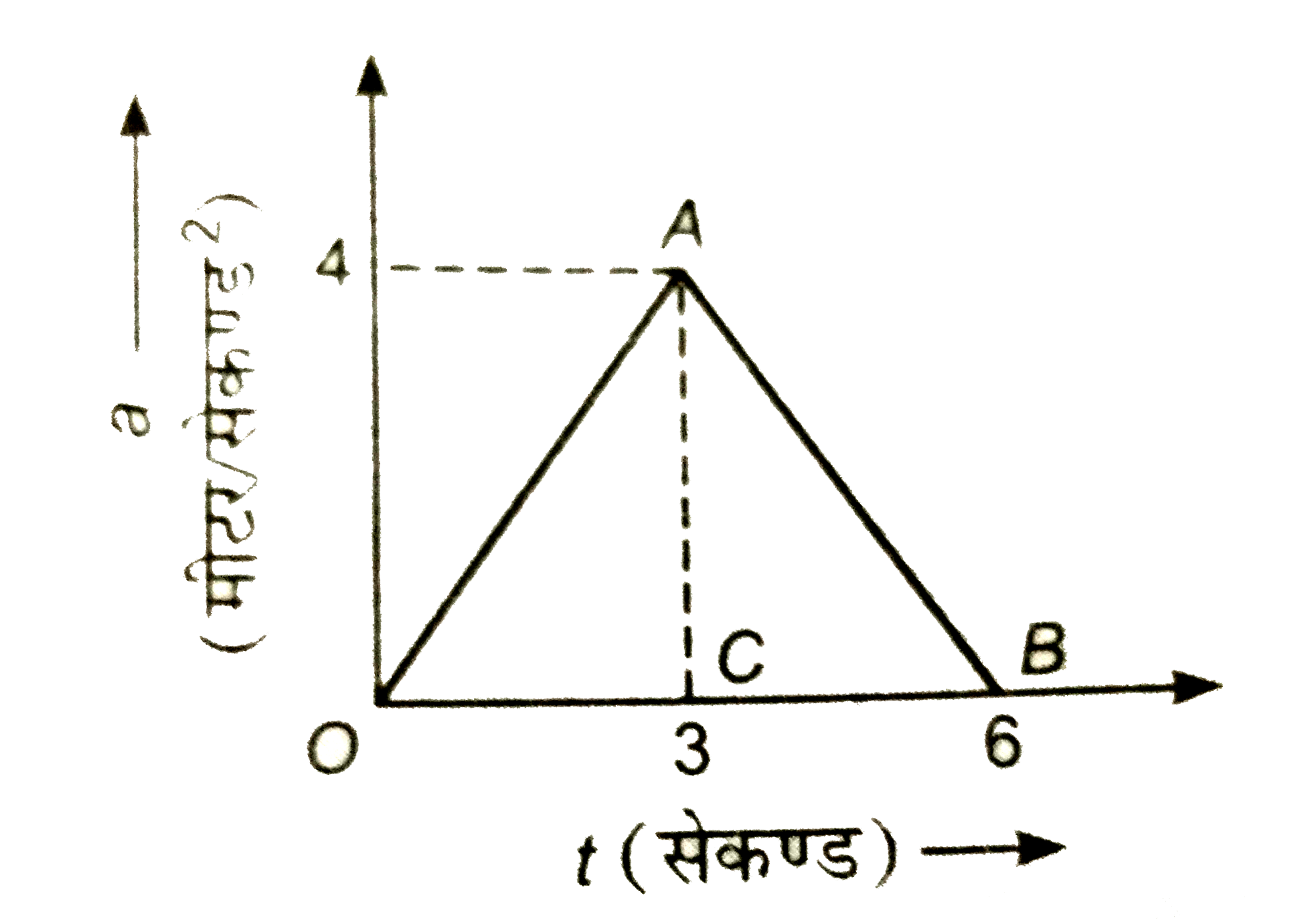
View Solutionसरल रेखा में गतिमान कण का क्षण t=0 सेकण्ड पर वेग 10 मीटर/सेकण्ड हैं कण एकसमान त्वरण 4मीटर/सेकण्ड2 के अन्तर्गत गतिमान है।
(i) t=3 से t=5 सेकण्ड के बीच कण का औसत वेग क्या है?
(ii) दूसरे सेकण्ड में कण का औसत वेग क्या है?
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View SolutionA particle moving along a straight line has the relation s=t3+2t+3, connecting the distance s describe by the particle in time t. Find the velocity and acceleration of the particle at t=4 sec.
View SolutionThe motion of a particle along a straight line is described by the function x = (2t-3)^(2) where x is in metres and t is in seconds . The acceleration of the particle at =2s is
View SolutionThe motion of a particle along a straight line is described by the function s=6+4t^(2)-t^(4) in SI units.Find the velocity ,acceleration ,at t=2s,and the average velocity during 3rd second.
View SolutionThe motion of a particle along a straight line is described by the function s=6+4t2−t4
in SI units.Find the velocity ,acceleration ,at t=2s,and the average velocity during 3rd second.
View SolutionThe motion of a particle along a straight line is described by the function s=6+4^(2)-t^(4) in SI units. Find the velocity, acceleration, at t=2s , and the average velocity during 3^(rd) seconds.
View Solution
