The motion of a particle along a straight line is described by the function s=6+4t2−t4
in SI units.Find the velocity ,acceleration ,at t=2s,and the average velocity during 3rd second.Solution in Telugu
s=6+4t2−t4
Velocity =dxdt=8t−4t3 when t-2
Velocity =8×2−4×23 Velocity =-16m/s
Acceleration a=d2sdt2=8 12t2 when t-2
acc =8−12×22=−40 a=−40m/s2
displacement in 3 seconds s2=6+4,32−34=−39m
displacment during 3rd second
Average velocity during 3rd second =+451=−45m/s
-ve sign indicates that the body is moving in opposite direction to the initial direction of motion.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise 1A
62 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Exercise 2A
30 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Questions for Descriptive Answers
7 Videos
- MOTION IN A PLANE BOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANE EXERCISE - Practice Exercise
84 Videos
- NEWTONS LAWS OF MOTION BOOK - AAKASH SERIESCHAPTER - NEWTONS LAWS OF MOTION EXERCISE - ADDITIONAL PRACTICE EXERCISE PRACTICE SHEET (ADVANECED) (Matrix Matching Type Questions)
1 Videos
Similar Questions
A particle starts from the origin ,goes along the x-axis to the point (20m,0) and then returns along the same line to the point (-20 m,0).The distance and displacement of the particle during the trip are
View Solution(A): Displacement of a body may be zero when distance travelled by it is not zero.
(R) : The displacement is the longest distance between initial and final positions..
View SolutionThree tortoises are located at the vertices of an equilateral triangle whose side equals a They all start moving simultaneously with velocity v constant in modulus with the first tortoise heading continually for the second , the second for the third and the third for the first . They will meet after time
View SolutionA person runs along a circular path of radius 5m. Find the magnitude of the displacement if he runs all the way around the circle ?
View SolutionThe system shown in the figure is given an acceleration 'a' towards left. Assume all contact surfaces to be smooth (m: mass of the sphere) The magnitude of the contact force between wedge and sphere between wedge and sphere at A is xmg√3 then 'x' is

View SolutionThe motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .
View SolutionThe velocity-time graph of a particle moving along a straight line is shown is . The rate of acceleration and deceleration is constant and it is equal to 5ms−2. If the a average velocity during the motion is 20ms−1, Then
 .
.
The value of t is.
View SolutionThe position of a particle moving on the x-axis is given by x=t^(3)+4t^(2)-2t+5 where x is in meter and t is in seconds (i) the velocity of the particle at t=4 s is 78 m//s (ii) the acceleration of the particle at t=4 s is 32 m//s^(2) (iii) the average velocity during the interval t=0 to t=4 s is 30 m//s (iv) the average acceleration during the interval t=0 to t=4 s is 20 m//s^(2)
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
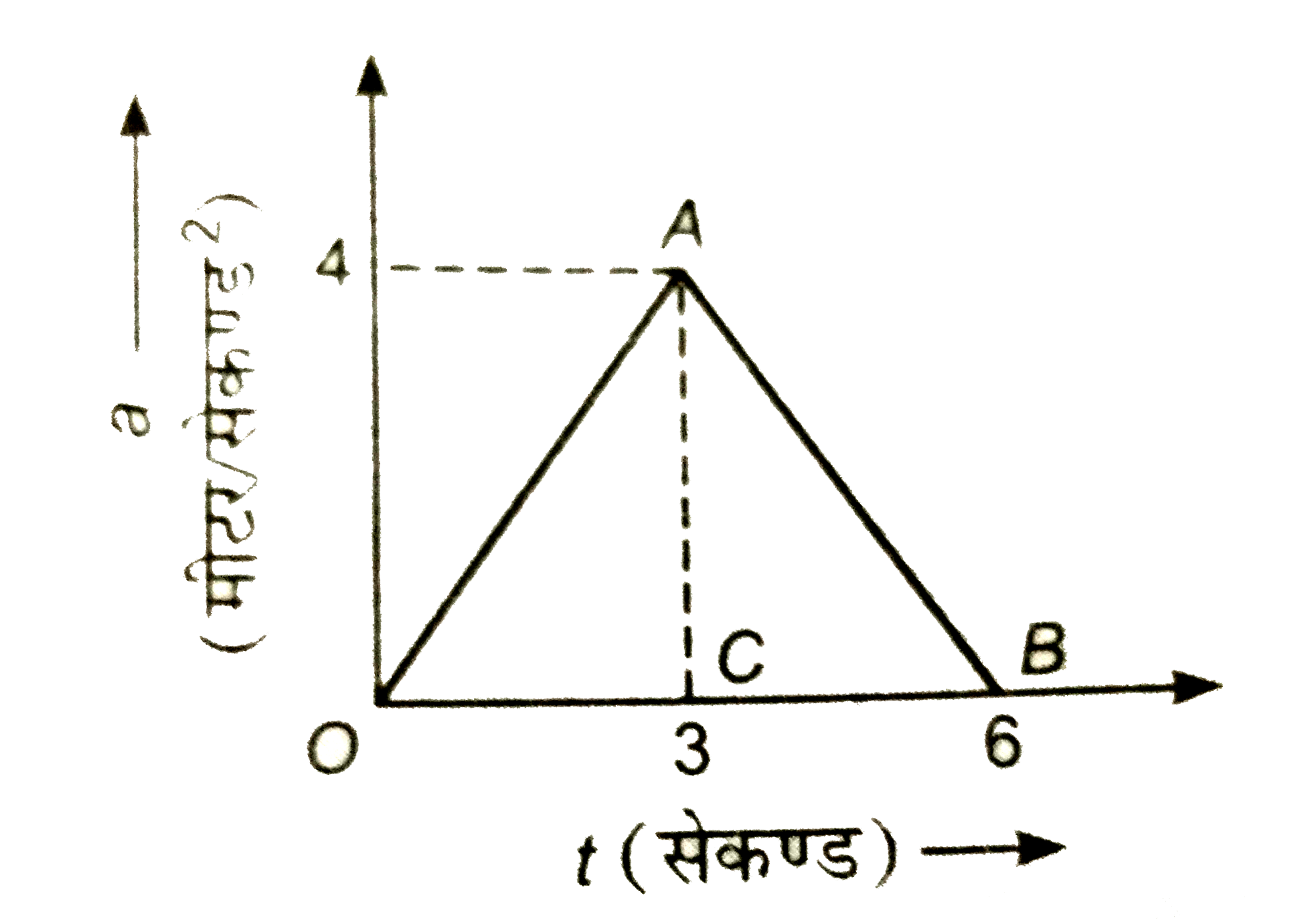
View Solutionसरल रेखा में गतिमान कण का क्षण t=0 सेकण्ड पर वेग 10 मीटर/सेकण्ड हैं कण एकसमान त्वरण 4मीटर/सेकण्ड2 के अन्तर्गत गतिमान है।
(i) t=3 से t=5 सेकण्ड के बीच कण का औसत वेग क्या है?
(ii) दूसरे सेकण्ड में कण का औसत वेग क्या है?
View SolutionThe velocity of a particle are given by (4t–2) ms–1 along x–axis. Calculate the average acceleration of particle during the time interval from t = 1 to t = 2s.
View SolutionThe motion of a particle along a straight line is described by the function x = (2t-3)^(2) where x is in metres and t is in seconds . The acceleration of the particle at =2s is
View SolutionThe motion of a particle along a straight line is described by the function s = 6 + 4t^2 - t^4 in SI units. Find the velocity, acceleration, at t = 2s, and the average velocity during 3^(rd) second.
View SolutionThe motion of a particle along a straight line is described by the function s=6+4t^(2)-t^(4) in SI units.Find the velocity ,acceleration ,at t=2s,and the average velocity during 3rd second.
View SolutionThe motion of a particle along a straight line is described by the function s=6+4^(2)-t^(4) in SI units. Find the velocity, acceleration, at t=2s , and the average velocity during 3^(rd) seconds.
View Solution
