The displacement x of a particle at the instant when its velocity v is given by v=√3x+16. Find its acceleration and initial velocity Solution in Telugu
v=√3x+16 or v2=3x+16
or v2−16=3x Comparing with v2−u2=2as
we get , u =4 units, 2a=3 or a=1.5 units .
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -I
58 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - EXERCISE -II
80 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
45 Videos
Similar Questions
The ratio of the numerical values of the average velocity and average speed of a body is always
View SolutionA person travels along a straight road for half the distance with velocity V1 and the remaining half distance with velocity V2 the average velocity is given by
View SolutionA particle is projected over a triangle from one end of a horizontal base and garzing the vertex falls on the other end of the base . If α and β the base angles and θ the angle of projection then show that tanθ=tanα+tanβ.
View SolutionA proton, a deuteron and an a particle having same momentum enter a uniform magnetic field at right angles to the field. Then the ratio of their angular momenta during their motion in the magnetic field is
View SolutionRefering to v−s diagram, find:
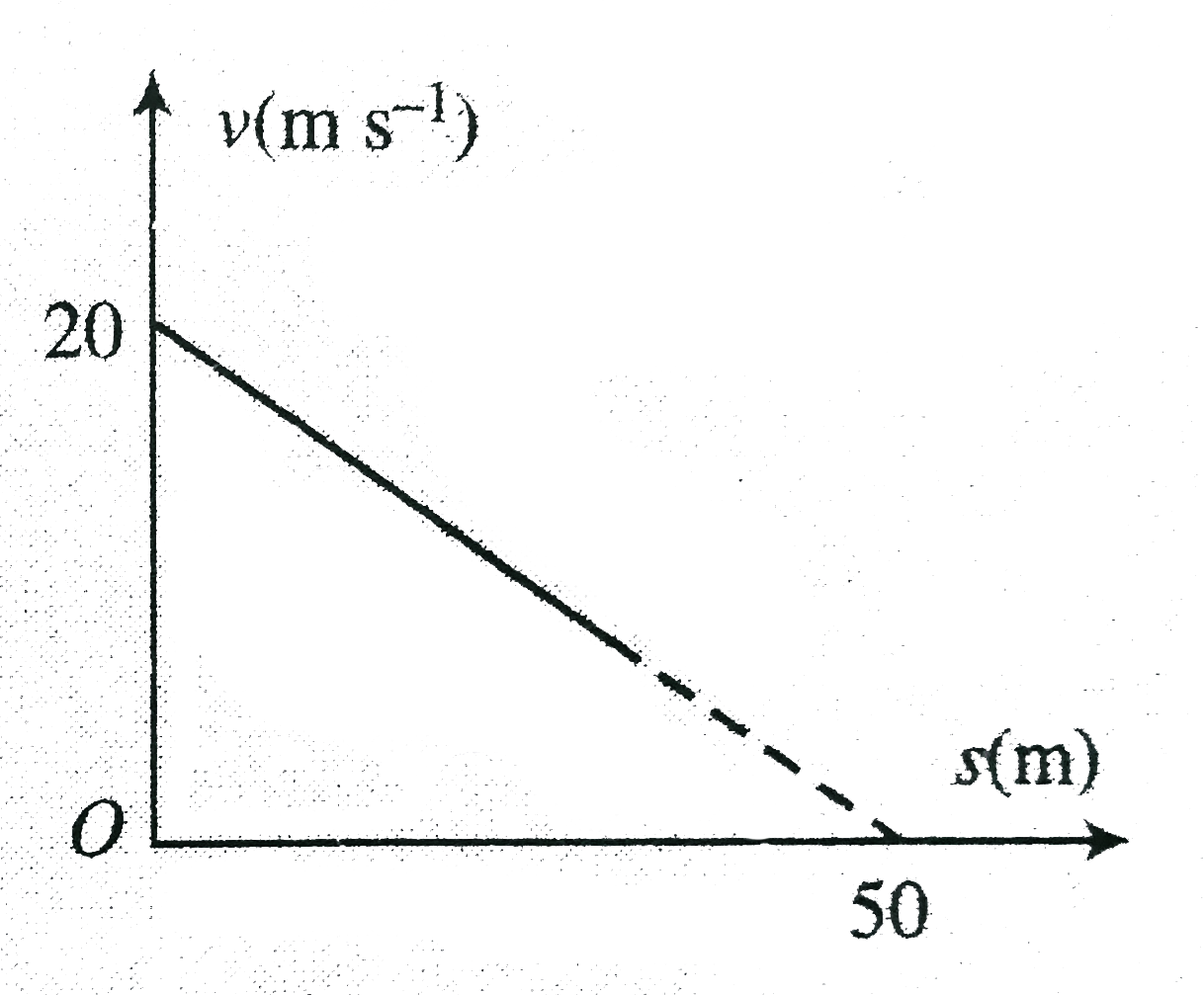 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.
View SolutionA particle is projected with a velocity u making an angle theta with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
View SolutionThe velocity of any particle is related with its displacement As, x = sqrt(v+1) , Calculate acceleration at x = 5m .
View SolutionThe velocity of particle is given by v=sqrt(gx) . Find its acceleration.
View Solution[" The displacement "x" of a particle at the "],[" instant when its velocity "v" is given by "],[v=sqrt(3x+16)" .Find its acceleration "],[[" (A) "1.5" units "],[" (B) "2.5" units "],[" (C) "3.5" units "],[" (D) "4.5" units "]]
View Solution" The displacement x of a particle at the instant when its velocity v is given by "v=sqrt(3x)+16" .Find its acceleration "
View SolutionThe velocity of a particle varies with its displacement as v=(√9−x2)ms−1.
Find the magnitude of the maximum acceleration of the particle.
View Solution" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
View SolutionThe displacement x of a particle at the instant when its velocity is v is given by v=sqrt(3x+16) . Its initial velociyt is
View SolutionIf the velocity "v" of a particle varies as the square of its displacement "x" then the acceleration varies as
View SolutionThe displacement x of a particle at the instant when its velocity v is given by v=√3x+16. Find its acceleration and initial velocity.
View Solution
