The displacement x of a particle at the instant when its velocity is v is given by v=√3x+16. Its initial velociyt is
To find the initial velocity of the particle given the relationship between displacement x and velocity v as v=√3x+16, we can follow these steps:
Step 1: Understand the relationship
The equation given is v=√3x+16. This means that the velocity v depends on the displacement x.
Step 2: Square both sides
To eliminate the square root, we square both sides of the equation:
v2=3x+16
Step 3: Rearrange the equation
Rearranging the equation to express x in terms of v:
3x=v2−16
x=v2−163
Step 4: Find initial conditions
The initial velocity corresponds to the condition when the particle starts moving. We need to find the value of v when x=0 (the displacement at the start).
Substituting x=0 into the rearranged equation:
0=v2−163
Step 5: Solve for v
Multiplying both sides by 3 gives:
0=v2−16
This simplifies to:
v2=16
Taking the square root of both sides, we find:
v=4orv=−4
Since we are looking for the initial velocity, we take the positive value:
v=4
Conclusion
Thus, the initial velocity of the particle is 4 units.
---
The equation given is v=√3x+16. This means that the velocity v depends on the displacement x.
To eliminate the square root, we square both sides of the equation:
v2=3x+16
Rearranging the equation to express x in terms of v:
3x=v2−16
x=v2−163
The initial velocity corresponds to the condition when the particle starts moving. We need to find the value of v when x=0 (the displacement at the start).
0=v2−163
Multiplying both sides by 3 gives:
0=v2−16
This simplifies to:
v2=16
Taking the square root of both sides, we find:
v=4orv=−4
v=4
Thus, the initial velocity of the particle is 4 units.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER -3 (MOTION IN PLANE)
Explore 15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER -4 (LAWS OF MOTION)
Explore 15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER 29 : (COMMUNICATION SYSTEMS)
Explore 15 Videos
- ATOMSBook:DISHA PUBLICATIONChapter:ATOMSExercise:EXERCISE-2: CONCEPT APPLICATOR
Explore 30 Videos
- COMMUNICATION SYSTEM Book:DISHA PUBLICATIONChapter:COMMUNICATION SYSTEM Exercise:EXERCISE-2 : Concept Applicator
Explore 30 Videos
Similar Questions
" The displacement x of a particle at the instant when its velocity v is given by "v=sqrt(3x)+16" .Find its acceleration "
View Solution[" The displacement "x" of a particle at the "],[" instant when its velocity "v" is given by "],[v=sqrt(3x+16)" .Find its acceleration "],[[" (A) "1.5" units "],[" (B) "2.5" units "],[" (C) "3.5" units "],[" (D) "4.5" units "]]
View Solution
Knowledge Check
In the above question what will be the displacement of particle in x-direction when its velocity makes 60∘ angle with initial velocity?
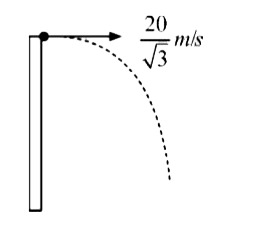 A20√3mB40√3mC50√3mD10√3m
A20√3mB40√3mC50√3mD10√3mAcceleration v/s displacement graph of a particle moving in a straight line is as shown in the figure. The initial velocity of the particle is zero. The velocity v/s displacement graph of the particle would be :
 A
A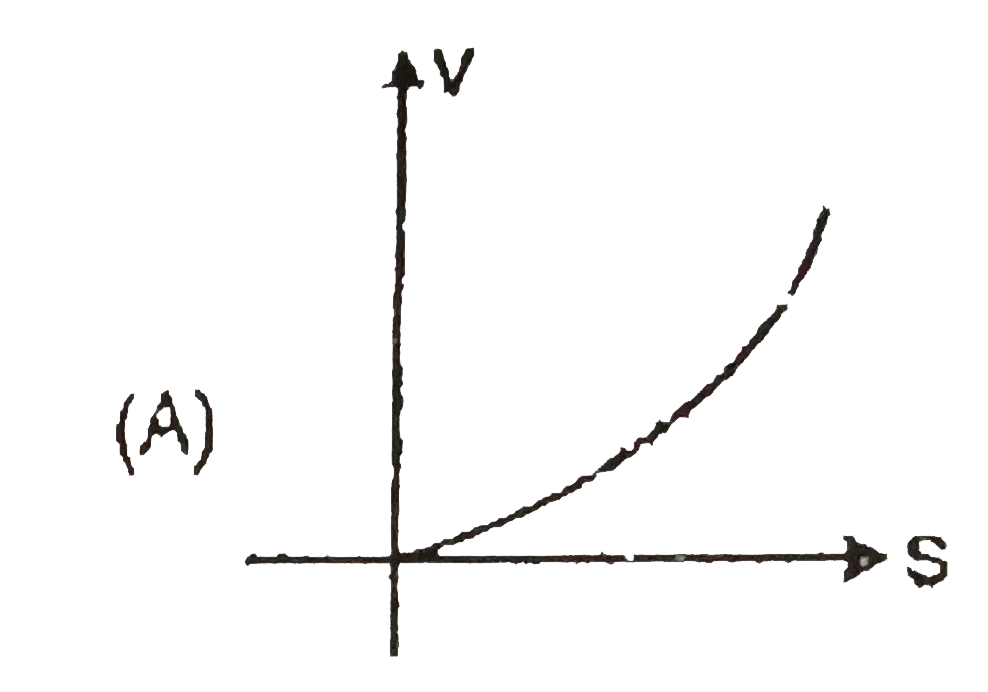 B
B C
C DNone of these
DNone of theseThe velocity of a particle at an instant is 10ms−1. After 3 s its velocity will becomes 16ms−1. The velocity at 2 s, before the given instant will be
A6ms−1B4ms−1C2ms−1D1ms−1
A moving body is opposed by a force per unit mass of value cx and resistance per unit mass of value bv2 where x and v are displacement and velocity of the particle at that instant. Find the velocity of the particle in terms of x, if its initial velocity is v0.
View SolutionThe velocity of particle is given by v=√gx . Find its acceleration.
View SolutionThe displacement of a particle along the x-axis is given by x=3+8t+7t2. Obtain its velocity and acceleration at t=2s.
View SolutionThe displacement x of a particle varies as
√x=t−2
(i) What is the velocity and acceleration of the particle at t=0?
(ii) When will the velocity of the particle become zero?
(iii) What is the displacement of the particle when its velocity is zero?
(iv) Is the motion of the particle uniformly accelerated or not?
View SolutionCalculate the acceleration of an object if its velocity is given by v=12(√12x+24)
View Solution

