Complete Solutions to NEET CAFÉ TOPICWISE PRACTICE QUESTIONS of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| MTG GUIDE | NEET CAFÉ TOPICWISE PRACTICE QUESTIONS |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
if the frequency of human heart is 1.25 Hz, the number of heart beats in 1 minutes is
View SolutionThe velocity of a particle executing simple harmonic motion is
View SolutionThe maximum speed of a particle executing SHM is 10 m/s and maximum acceleration is `31.4m//s^(2)`. Its periodic time is
View SolutionIf the displacement (x) and velocity (v) of a particle executing simple harmonic motion are related through the expression `4v^2=25-x^2`, then its time period is given by
View SolutionA particle executing of a simple harmonic motion covers a distance equal to half its amplitude in on e second . Then the time period of the simple harmonic motion is
View SolutionA particle makes simple harmonic motion in a straight line 4 cm long. Its velocity while passing through the centre of the line is `16 cm s^(-1)`. The period of the oscillation is
View SolutionA simple harmonic oscillation has an amplitude `A` and time period `T`. The time required to travel from `x = A` to ` x= (A)/(2)` is
View SolutionTime period of a particle executing `SHM` is `8` sec. At `t=0` it is at the mean position. The ratio of the distance covered by the particle in the `1st` second to the `2nd` second is:
View SolutionA particle executes linear simple harmonic motion with an amplitude of 2 cm . When the particle is at 1 cm from the mean position the magnitude of its velocity is equal to that of its acceleration. Then its time period in seconds is
View SolutionA point mass oscillates along the `x-`acis according to the law `x = x_(0)cos(omegat - pi//4)` if the acceleration of the particle is written as, a `= A cos(omega + delta)`, then :
View SolutionThe maximum velocity a particle, executing simple harmonic motion with an amplitude 7 mm, 4.4 m//s. The period of oscillation is.
View SolutionThe displacement of a particle executing S.H.M. is given by y = 0.25 sin 200t cm. The maximum speed of the particle is
View SolutionThe potential energy of a particle of mass `1kg` in motion along the x- axis is given by: `U = 4(1 - cos 2x)`, where `x` in meters. The period of small oscillation (in sec) is
View SolutionA particle executing harmonic motion is having velocities `v_1` and `v_2` at distances is `x_1` and `x_2` from the equilibrium position. The amplitude of the motion is
View SolutionA particle of mass (m) is executing oscillations about the origin on the (x) axis. Its potential energy is `V(x) = k|x|^3` where (k) is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionThe displacement of a particle from its mean position (in metre) is given by
`y=0.2 "sin" (10 pi t+ 1.5 pi) "cos" (10 pi t+1.5 pi)`
The motion of the particle is
View SolutionA particle is executing simple harmonic motion of amplitude 5 cm and period 6 s. How long will it take to move from one end of its path on one side of mean position to a position 2.5 cm on the same side of the mean position ?
View SolutionWhich of the following relationship between the acceleration, a and the displacement x of a particle involve simple harmonic motion.
(a) `a=7.0x` (b) `a=-200x^(2)` (c) `a=-10x` (d) `a=100x^(3)`
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)` sinomegat-cosomegat` (ii) `sin^(2)omegat` (iii) `cosomegat+2sin^(2)omegat`
View SolutionIf `f(x) =(x-x_(0)) phi (x) and phi (x)` is continuous at `x=x_(0)` then what is `f(x_(0))` equal to ?
View SolutionThe angular velocities of three bodies in `SHM` are `omega_(1), omega_(2), omega_(3)` with their respective amplitudes as `A_(1),A_(2),A_(3)`. If all three bodies have same mass and maximum velocity then
View SolutionTwo simple harmonic motions are represented by the equations
`y_(1) = 10 sin(3pit + pi//4) and y_(2) = 5(sin 3pit + sqrt(3)cos 3pit)` their amplitude are in the ratio of ………… .
View SolutionA particle executes SHM of type `x=Asinomegat`. It takes time `t_(1)` from `x=0` to `x=(A)/(2) and t_(2)` from `x=(A)/(2)` to `x=A`. The ratio `t_(1):t_(2)` will be
View SolutionThe `x-t` graph of a particle undergoing simple harmonic motion is shown in figure. Acceleration of particle at `t = 4//3 s` is
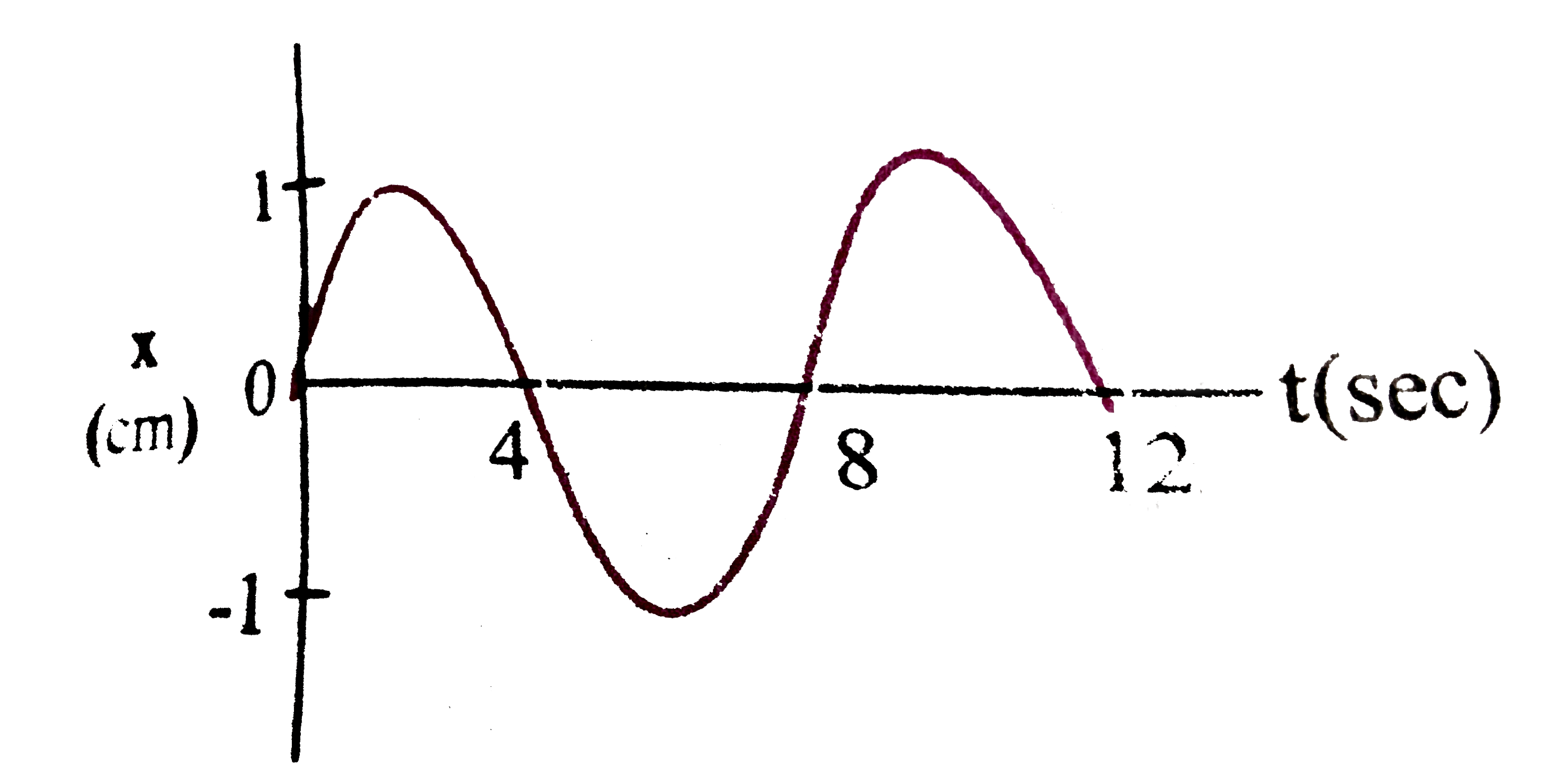
View SolutionThe equation of motion of a particle executing simple harmonic motion is `a+16pi^(2)x = 0` In this equation, a is the linear acceleration in `m//s^(2)` of the particle at a displacement x in meter. The time period in simple harmonic motion is
View SolutionWhich of the following motions is not simple harmonic?
View SolutionA particle is executing simple harmonic motion with an amplitude A and time period T. The displacement of the particles after 2T period from its initial position is
View SolutionIf `x, v` and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period `T`, then, which of the following does not change with time ?
View SolutionA particle executing SHM is described by the displacement function `x(t)=Acos(omegat+phi)`, if the initial (t=0) position of the particle is 1 cm, its initial velocity is `pii" cm "s^(-1)` and its angular frequency is `pis^(-1)`, then the amplitude of its motion is
View SolutionIn SHM, kinetic energy is `(1//4)^(th)` of the total energy at a displacement equal to
(Here A is the amplitude of oscillations.)
View SolutionIf `ltTgt and ltUgt` denote the average kinetic and the average potential energies respectively of a mass executing a simple harmonic motion over one period, then the corresponding relation is
View SolutionStarting from the origin a body osillates simple harmonicall with a period of 2 s. A fter what time will its kinetic energy be 75% of the total energy?
View SolutionAn object of mass `0.2 kg` executes simple harmonic oscillation along the `x - axis`with a frequency of `(25//pi) Hz`. At the position `x = 0.04`, the object has Kinetic energy of `0.5 J` and potential energy `0.4 J. The amplitude of oscillations is……m.
View SolutionA certain simple harmonic vibrator of mass 0.1 kg has a total energy of 10 J. Its displacement from the mean position is 1 cm when it has equal kinetic and potential energies. The amplitude A and frequency n of vibration of the vibrator are
View SolutionA particle of mass m executes simple harmonic motion with amplitude a and frequency v. The average kinetic energy during its motion from the position of equilibrium to the ends is
View SolutionThe kinetic energy of paritcle executing SHm will be equal to `((1)/(8))^(th)` of its potential energy when its displacement from the mean position is (Where A is the amplitude) :
View SolutionA particle starts oscillating simple harmonically from its equilibrium position then, the ratio of kinetic energy and potential energy of the particle at the time `T//12` is: `(T="time period")`
View SolutionThe frequency of the mass when it is displaced slightly is

View SolutionTwo masses m1 and m2 are suspended together by a massless spring of constant k. When the masses are in equilibrium, m1 is removed without disturbing the system. The amplitude of oscillations is

View SolutionTwo springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are `k_(1) and k_(2)`, shown that frequency of oscillation of mass m is

View SolutionA particle of mass 'm' is attached to three identical springs `A,B` and `C` each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
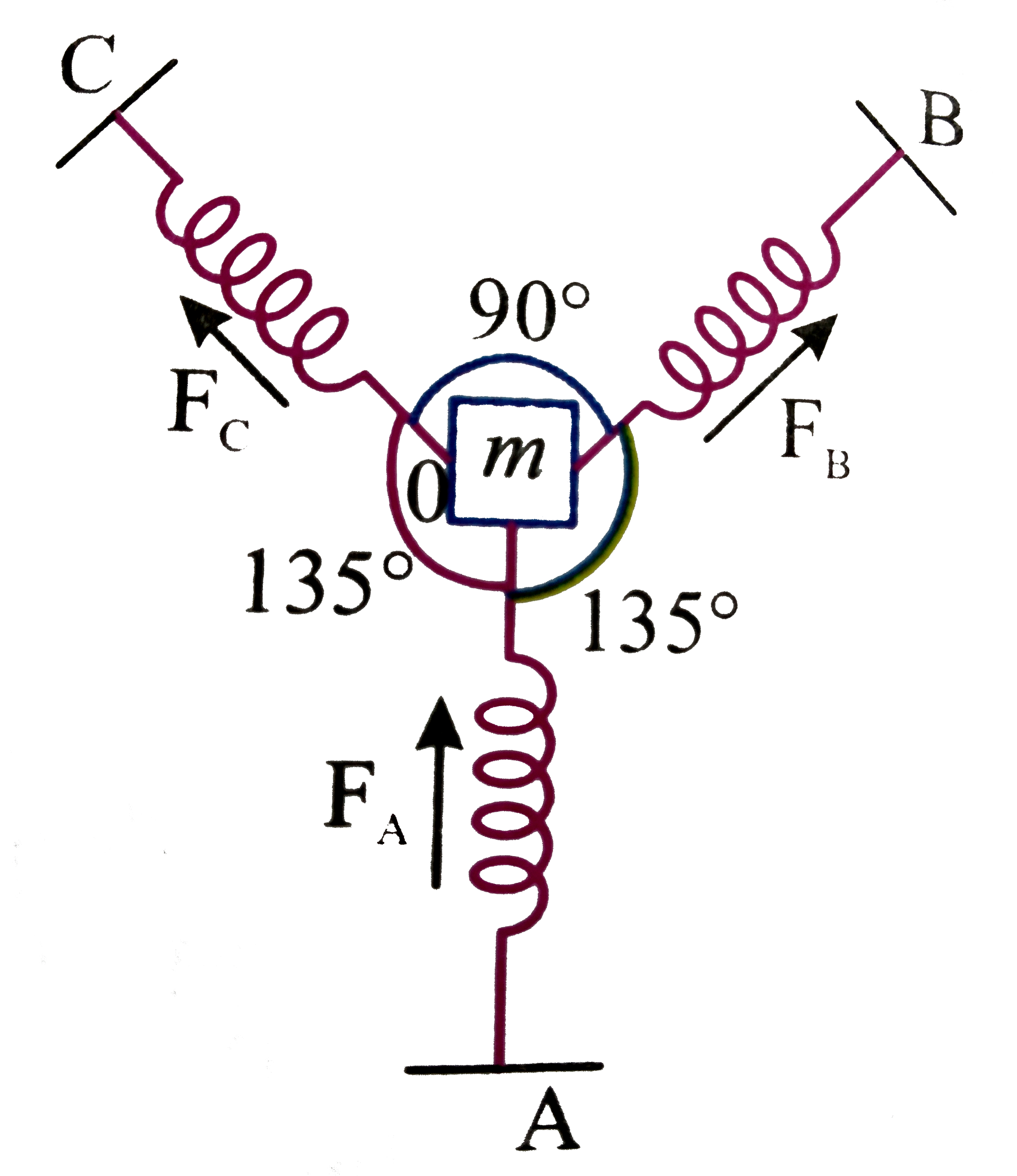
View SolutionA mass is suspended separately by two different springs in successive order, then time periods is `t_(1) "and" t_(2)` respectively. It is connected by both springs as shown in fig. then time period is `t_(0)`. The correct relation is
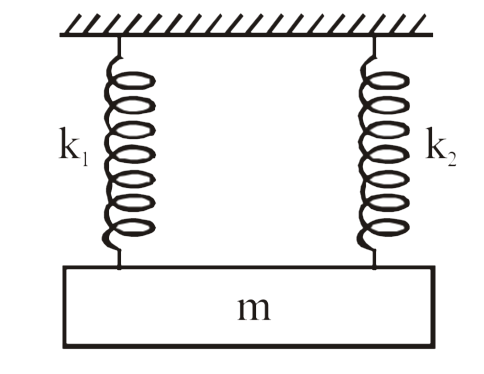
View SolutionA verticle mass-spring system executed simple harmonic ascillation with a period `2s` quantity of this system which exhibits simple harmonic motion with a period of `1sec` are
View SolutionA spring of force constant k is cut into two pieces such that one piece is double the length of the other. Then the long piece will have a force constant of :
View SolutionOn a smooth inclined plane, a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has force constant K , the period of oscillation of the body (assuming the springs as massless) is

View SolutionA system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
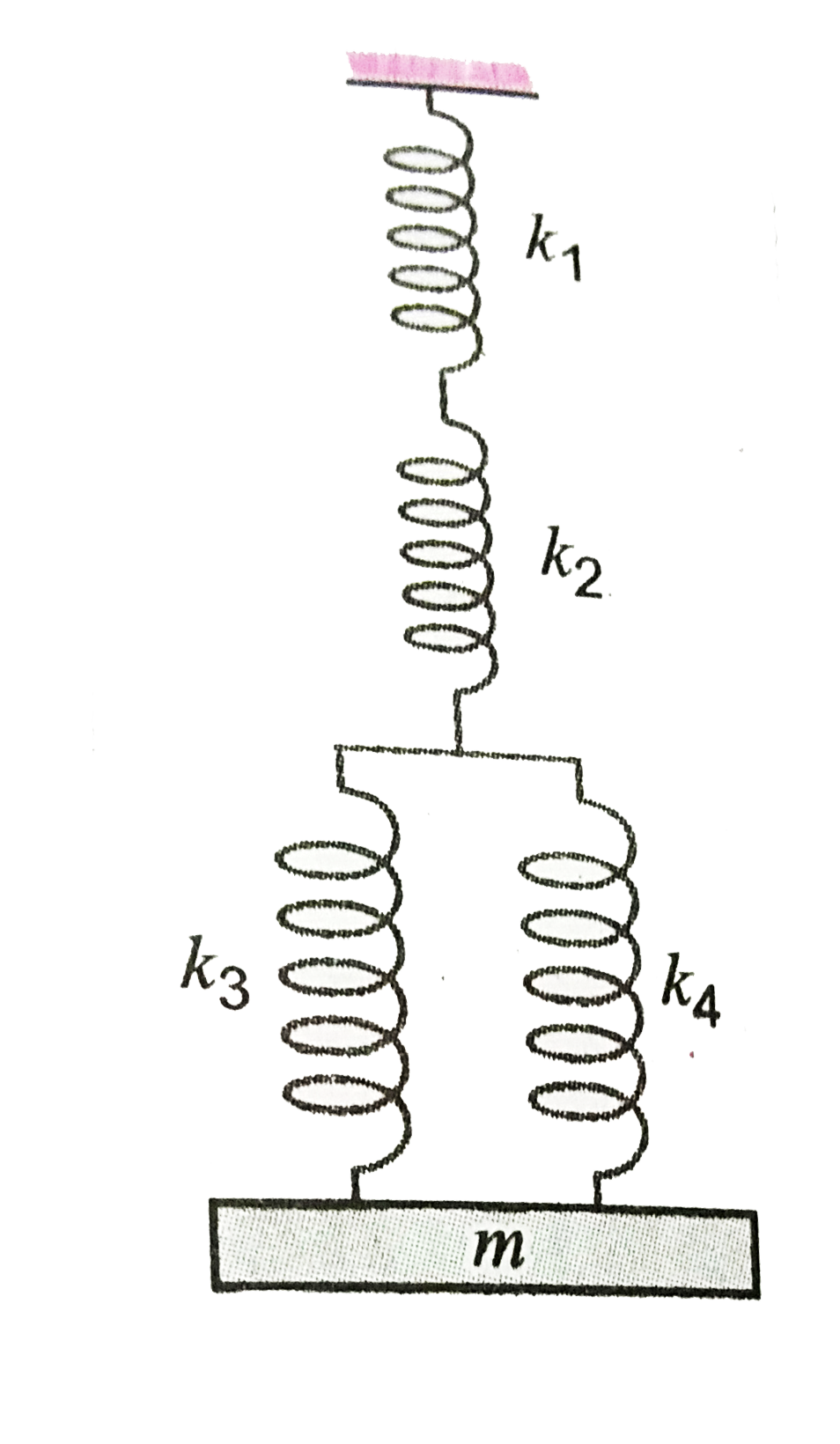
View SolutionIn figure `S_(1)` and`S_(1)` are identical springs. The oscillation frequency of the mass `m` is `f`. if one spring is removed, the frequency will become
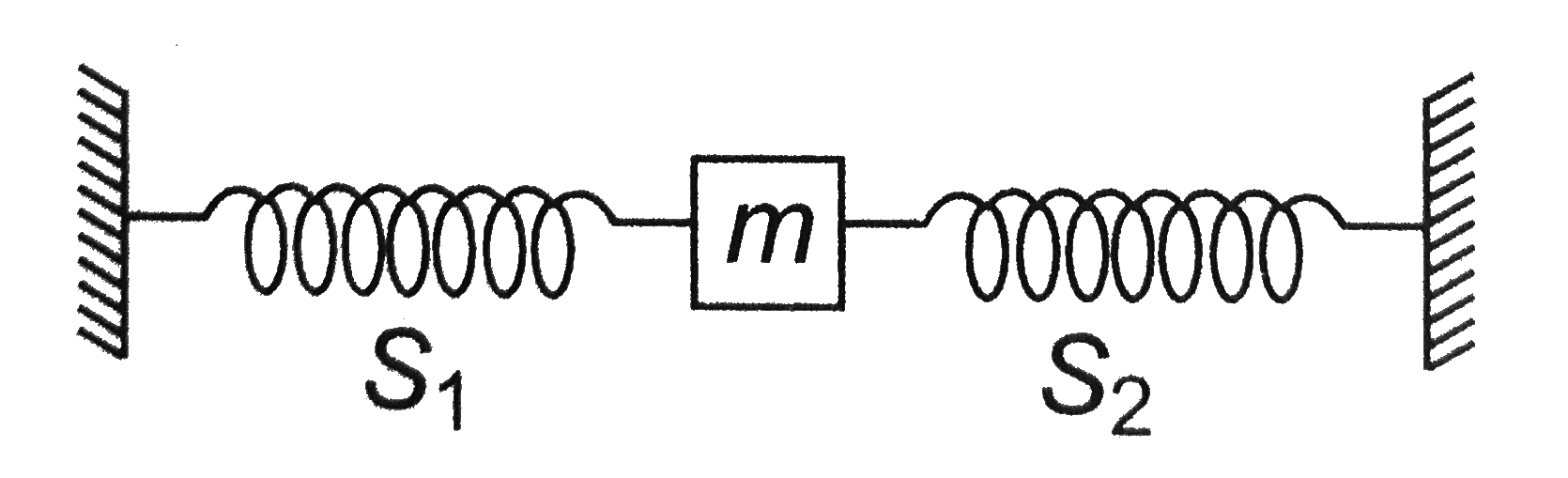
View SolutionTwo point masses of 3 kg and 6 kg are attached to opposite ends of horizontal spring whose spring constant is `300 Nm^(-1)` as shown in the figure. The natural vibration frequency of the system is approximately
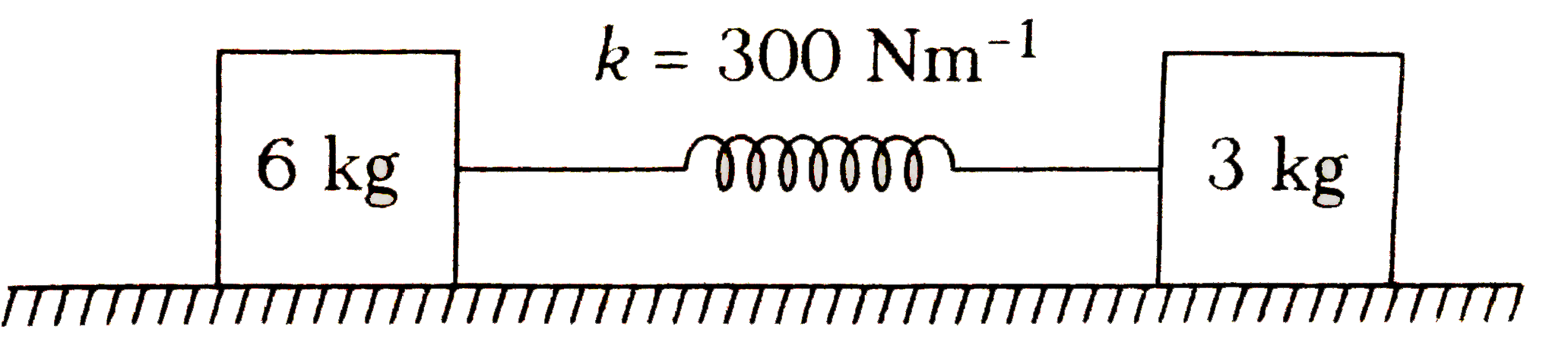
View SolutionIf a spring of force constant k is divided into n equal parts , then force constant of each part is
View SolutionTwo springs of constants `k_1` and `k_2` have equal maximum velocities, when executing simple harmonic motion. The ratio of their amplitudes (masses are equal) will be
View SolutionThe length of a spring is `alpha` when a force of `4N` is applied on it and the length is `beta` when `5N` is applied. Then the leng of spring when `9 N` force is applied is-
View SolutionLet `T_(1) and T_(2)` be the periods of springs A and B when mass M is suspended from one end of each spring. If both springs are taken in series and the same mass M is, suspended from the séries combination, the time period is T, then
View SolutionA mass M is attached to a horizontal spring of force constant k fixed one side to a rigid support as shown in figure. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass M is in equilibrium position, another mass m is gently placed on it. When will be the new amplitude of ocillation?
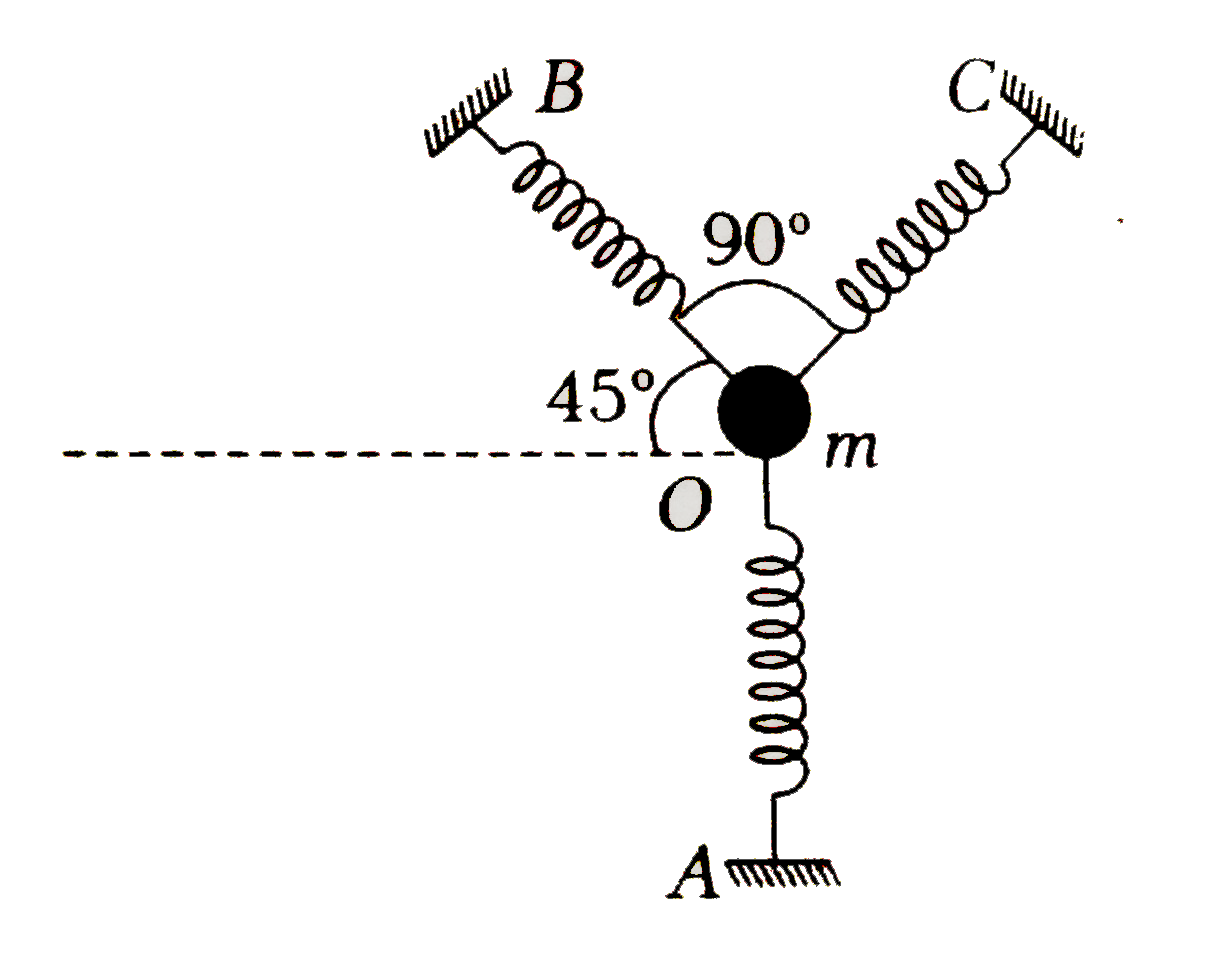

View SolutionA particle of mass 0.1 kg is held between two rigid supports by two springs of force constant `8 N m^(-1) and 2 N m^(-1)`. If the particle is displaced along the direction of length of the springs, its frequency of vibration is
View SolutionA weightless spring of length 60 cm and force constant `200 N m^(-1)` is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
View SolutionOne end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
View SolutionFour massless springs whose force constants are `2k, 2k, k` and `2k` respectively are attached to a mass `M` kept on a fricaionless plane (as shown in figure). If the mass `M` is displaced in the horizontal directions, then the frequency of the system.
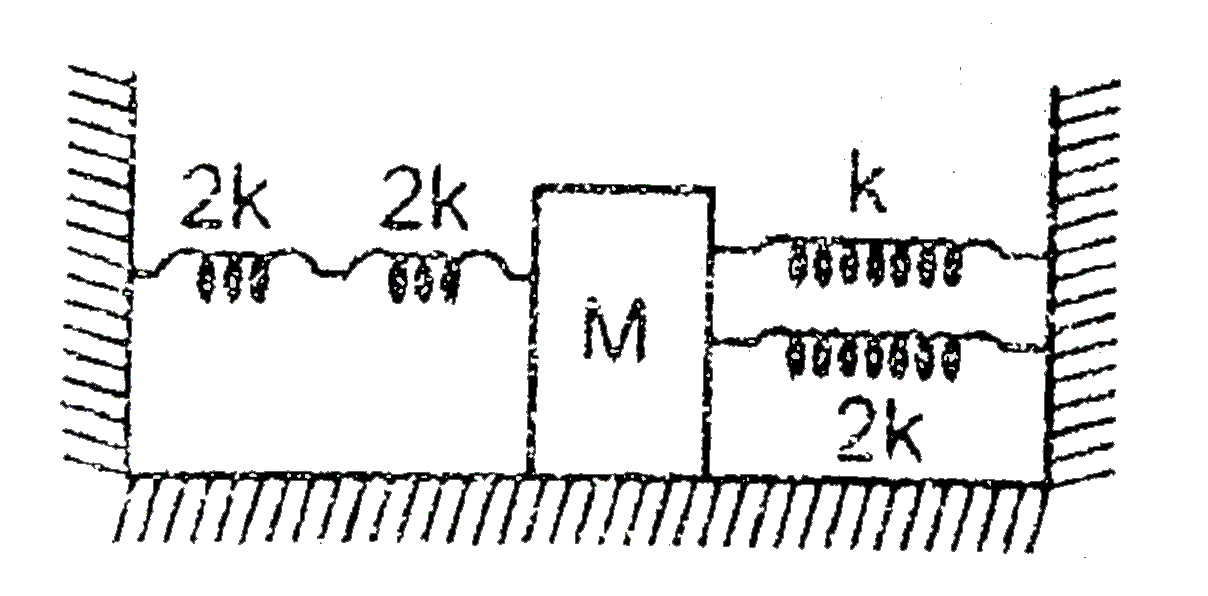
View SolutionThe mass M shown in figure ocillates in simple harmonic motion with amplitude A.
The amplitude of the point P is
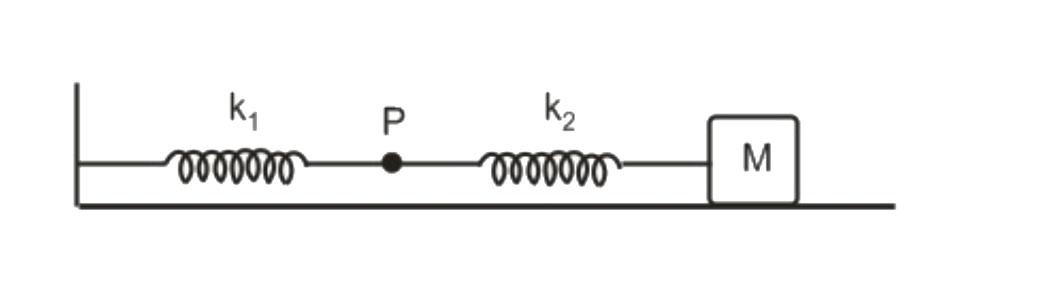
View SolutionAn electric motor of mass 40 kg is mounted on four vertical springs each having spring constant of `4000 N m^(-1)`. The period with which the motor vibrates vertically is
View SolutionA metal wire of length `L_1` and area of cross section A is ttached to a rigid support. Another metal wire of length `L_2` and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if `Y_1` and `Y_2` are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
View SolutionA body of mass 4.9 kg hangs from a spring and oscillates with a period 0.5 s. On the removal of the body, the spring is shortened by (Take `g=10m s^(-2), pi^(2)=10`)
View SolutionA mass of 4 kg suspended from a spring of spring constant `800 Nm^(-1)` executes simple harmonic oscillations. If the total energy of the oscillator is 4 J, the maximum acceleration (in `ms^(-2)`) of the mass is
View SolutionA trolley moves in horizontal direction with an acceleration a. A simple pendulum of length l is suspended from the roof of the trolley. The time period of the pendulum will be
View SolutionIf the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
View SolutionA pendulum suspended from the roof of an elevator at rest has a time period `T_(1)`, when the elevator moves up with an acceleration `a` its time period becomes `T_(2)`, when the elevator moves down with an acceleration `a`, its time period becomes `T_(3)`, then
View SolutionWhat is the length of a simple pendulum which ticks second?
View SolutionA simple pendulum has a time period `T_(1)` when on the earth's surface and `T_(2)` when taken to a height R above the earth's surface, where R is the radius of the earth. The value of `(T_(2))/(T_(1))` is
View SolutionTwo simple pendulums have time periods `T` and `5T//4`. They start vibrating at the same instant from the mean position in the same phase. The phase difference between them when the pendulum with higher time period complets one oscillation is
View SolutionA man measures the period of a simple pendulum inside a stationary lift and finds it to be T sec. if the lift accelerates upwards with an acceleration g/4, then the period of the pendulum will be
View SolutionThe acceleration due to gravity on the surface of the moon is `1.7ms^(-2)`. What is the time perioid of a simple pendulum on the surface of the moon, if its time period on the surface of earth is `3.5s ?` Take `g=9.8ms^(-2)` on the surface of the earth.
View SolutionThe length of second pendulum is 1 m on earth. If mass and diameter of the planet is doubled than that of earth, then length becomes
View SolutionA simple pendulum has a length `l`, mass of bob `m`. The bob is given a charge `q`.The pendulum is suspended between the vertical plates of charged parallel plate capacitor. If `E` is the field strength between the plates ,then time period `T = `
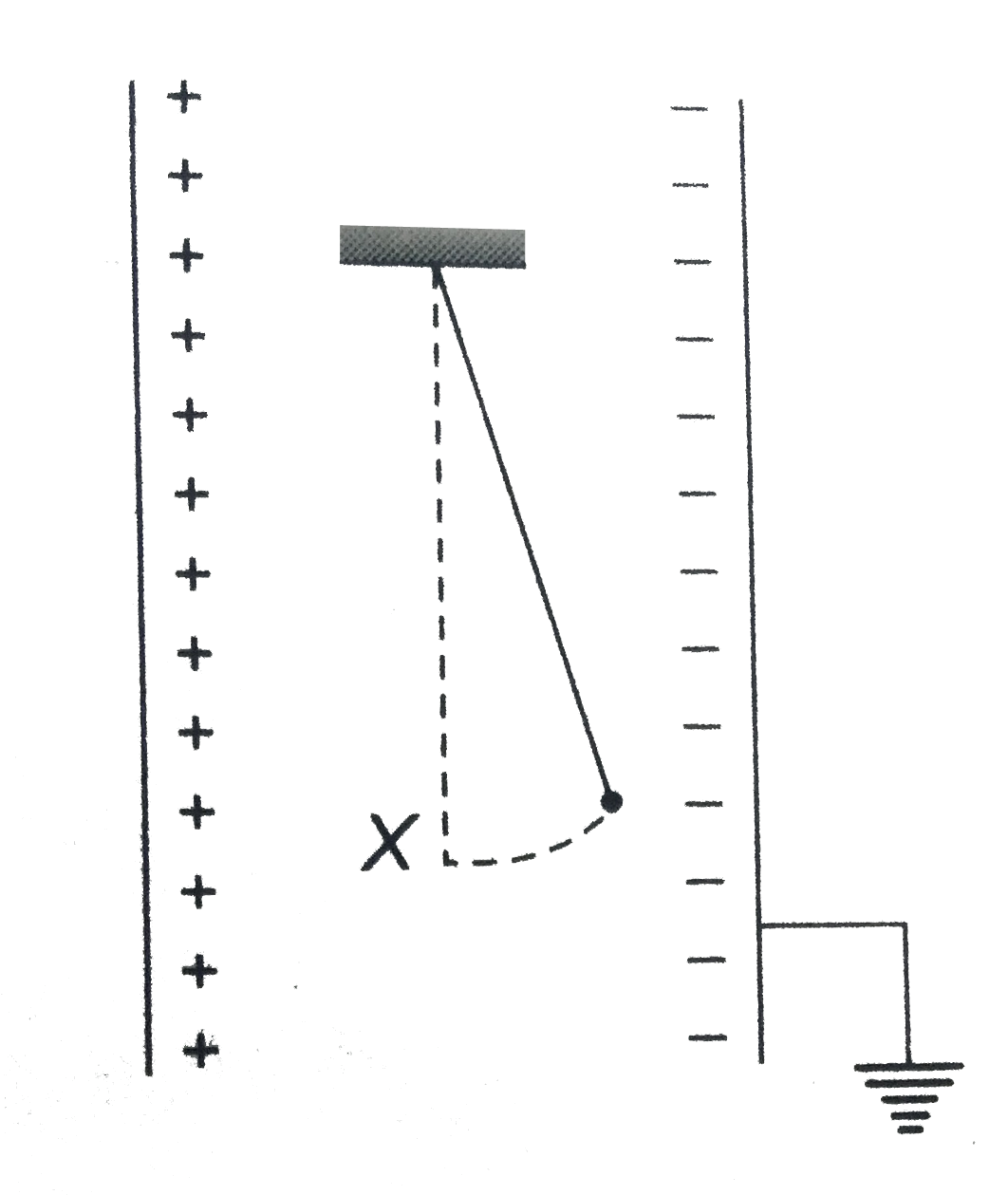
View SolutionTime period of a simple pendulum of length L is `T_(1)` and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is `T_(2)`. Amplitude of osciallations in both the cases is small. Then `T_(1)/T_(2)` is
View SolutionWhat effect occurs on the frequency of a pendulum if it is taken from the earth surface to deep into a mine
View SolutionA simple pendulum has time period (T_1). The point of suspension is now moved upward according to the relation `y = K t^2, (K = 1 m//s^2)` where (y) is the vertical displacement. The time period now becomes (T_2). The ratio of `(T_1^2)/(T_2^2)` is `(g = 10 m//s^2)`.
View SolutionThe bob of simple pendulum executes SHM in water with a period T, while the period of oscillation of the bob is `T_(0)` in air. Neglecting frictional force of water and given that the density of the bob is `(4000)/(3)kgm^(-3)` , find the ration between T and `T_(0)`.
View SolutionA disc of radius `R=10cm` oscillates as a physical pendulum about an axis perpendicular to the plane of the disc at a distance r from its centre. If `r=(R )/(4)`, the approximate period of oscillation is (Take `g=10ms^(-2)`)
View SolutionThere is a rod of length `l` and mass `m`. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionWhen an oscillator completes `100` oscillations its amplitude reduced to `(1)/(3)` of initial values. What will be amplitude, when it completes `200` oscillations :
View SolutionThe amplitude of damped oscillator becomes `1/3` in `2s`. Its amplitude after `6s` is `1//n` times the original. The value of `n` is
View SolutionA particle oscillating under a force `vecF=-kvecx-bvecv` is a (k and b are constants)
View SolutionResonance is an example of
View SolutionIn case of force oscillations of a body
View SolutionA wave is represented by the equation, `y = 0.1 sin (60 t + 2x)`, where x and y are in metres and t is in seconds. This represents a wave
View SolutionA wave is represented by `y=0.4cos(8t-(x)/(2))` where x and y are in metres and t in seconds. The frequency of the wave is
View SolutionThe equation of a wave travelling in a string can be written as ` y=3cos pi ( 100 t- x) .` Its wavelength is
View SolutionIn a sinusoidal wave, the time required for a particular point to move from maximum displacement to zero displacement is 0.170 second. The frequency of the wave is
View SolutionA wave travelling along the x-axis is described by the equation `v(x, t) = 0.005 cos(alpha x - betat)`. If the wavelength and the time period of the wave are `0.08m` and `2.0s`, respectively, then `alpha and beta` in appropriate units are
View SolutionWhat is the wavelength of wave shown in given figure?
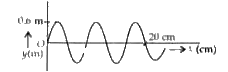
View SolutionThe particles of a medium vibrate about their mean positions whenever a wave travels through that medium. The phase difference between the vibrations of two such particles
View SolutionConsider a wave rpresented by `y= a cos^(2) (omega t-kx)` where symbols have their usual meanings. This wave has
View SolutionA string of linear density 0.2 kg/m is stretched with a force of 500 N. A transverse wave of length 4.0 m in set up along it. The speed of wave is
View SolutionThe eqyation of wave is ` x= 5sin ((t)/( 0.4) -( x)/(4))cm ` the maximum velocity of the particles of the medium is
View SolutionA progressive wave of frequency 500Hz is travelling with a velocity of 360 m`//` s. How far part are two points `60^(@)` out of phase ?
View SolutionIf the distance between successive compressions and rarefactions is 1 m and velocity of sound is `360 m s^(-1)`, then the frequency is
View SolutionIn brass the velocity of longitudinal wave is 100 times the velocity of transverse wave if `Y=1xx10^11N//m^2`, then stress in the wire is
View SolutionFigure shows the shape of part of a long string in which transverse waves are produced by attaching one end of the string to tuning fork of frequency 250 Hz. What is the velocity of the waves?
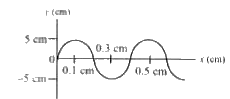
View SolutionThe displacement y of a wave travelling in the x-direction is given by
`y = 10^(-4) sin (600t - 2x + (pi)/(3)) m`
Where x is expressed in metre and t in seconds. The speed of the wave motion in m/s is
View SolutionThe linear density of a vibrating string is `10^(-4) kg//m`. A transverse wave is propagating on the string, which is described by the equation `y=0.02 sin (x+30t)`, where x and y are in metres and time t in seconds. Then tension in the string is
View SolutionA uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
View Solution
NEET CAFÉ TOPICWISE PRACTICE QUESTIONS questions and complete solutions for chapter OSCILLATIONS AND WAVES of MTG GUIDE PHYSICS (HINGLISH) of Class 11