Complete Solutions to ILLUSTRATION of chapter OSCILLATIONS AND WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS AND WAVES |
| MTG GUIDE | ILLUSTRATION |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
A particle executes SHM of period 1.2 s and amplitude 8 cm. find the time it takes to travel 3 cm the positive extremity of its oscillation. Given `cos^(-1)(0.625)=51^(@)`.
View SolutionTwo simple harmonic motion of angular frequency `100and 1000 rads^(-1)` have the same displacement amplitude The ratio of their maximum acceleration is
View Solution`x` and `y` displacements of a particle are given as `x(t)=-asinomegat` and `y(t)=asin2omegat`. Its trajectory will look like.
View SolutionA mass (M) is suspended from a spring of negligible mass. The spring is pulled a little and then released so that the mass executes SHM of time period T. If the mass is increased by m, the time period becomes `(5T)/3`. Then the ratio of `m/M` is .
View SolutionAt equilibrium, the springs are released, mass M is oscillating under the influence of three springs, `k_(1),k_(2)andk_(3)` as shown. Its frequency `(upsilon)` of oscillation is `(1)/(2pi)sqrt((k_(eq))/(M))`, where `k_(eq)` I such that
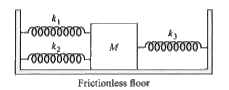
View SolutionTwo bodies A and B of equal mass are suspended from two separate massless springs of spring constant `k_1 and k_2` respectively. If the bodies iscillte vertically such that their maxixum velocities are equal, the ratio of the amplitude of A to that of B is
View SolutionTwo springs of force constants `k_(1)` and `k_(2)`, are connected to a mass m as shown. The frequency of oscillation of the mass is `f`. If both `k_(1)` and `k_(2)` are made four times their original values, the frequency of oscillation becomes
_E01_383_Q01.png)
View SolutionIf `E_(P)andE_(K)` represent the potential energy and kinetic energy of a body undergoing S.H.M, then (E is the total energy of the body), at a position where the displacement is half the amplitude.
View SolutionThe total mechanical energy of a spring mass system in simple harmonic motion is `E=1/2momega^2 A^2`. Suppose the oscillating particle is replaced by another particle of double the mass while the amplitude A remains the same. The new mechanical energy will
View SolutionStarting from the origin a body osillates simple harmonicall with a period of 2 s. A fter what time will its kinetic energy be 75% of the total energy?
View SolutionA simple pendulum is set up on a trolley which slides down a frictionless inclined plane making an angle `theta` with horizontal. The time period of pendulum is
View SolutionA simple pendulum is suspended from the roof of a trolley which moves in a horizontal direction with an acceleration `alpha`, then the time period is given by `T = 2pisqrt(((I)/(T)))` where g is equal to
View SolutionA simple pendulum of length `l_(1)` has a time period of 4 s and another simple pendulum of length `l_(2)` has a time period 3 s. Then the time period of another pendulum of length `(l_(1)-l_(2))` is
View SolutionThe displacement of a particle of a string carrying a travelling wave is given by `y=(4cm)sin2pi(0.5x-100t)`, where x is in cm and t is in seconds. The speed of the wave is
View SolutionThe displacement of a wave disturbance propagating in the positive x-direction is given by
`y =(1)/(1 + x^(2))`at `t = 0` and `y =(1)/(1 +(x - 1)^(2))` at `t =2s`
where, `x` and `y` are in meter. The shape of the wave disturbance does not change during the propagation. what is the velocity of the wave?
View SolutionThe disperod of a particle varies according to the relation `x=4 (cos pit+ sinpit)`. The amplitude of the particle is.
View SolutionThe displacement of a particle executing S.H.M. is given by `y = 10 sin [6t + (pi)/(3)]` where y is in metres and t is in seconds. Then the initial displacement and velocity of the particle is
View SolutionA traverse wave is repersented by the equation
`y=y_(0)sin(2pi)/(lambda)(vt-x)`
For what value of `lambda` the maximumn particle velocity equal to two times the wave velocity
View SolutionA uniform rope of length 10 m and mass 3 kg hangs vertically from a rigid support. A block of mass 1 kg is attached to the free end of the rople. A transverse pulse of wavelength 0.05 m is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is
View SolutionThe vibrations of a string fixed at both ends are described by the equation `y= (5.00 mm) sin [(1.57cm^(-1))x] sin [(314 s^(-1))t]`
(a) What is the maximum displacement of particle at x = 5.66 cm ? (b) What are the wavelengths and the wave speeds of the two transvers waves that combine to give the above vibration ? (c ) What is the velocity of the particle at x = 5.66 cm at time t = 2.00s ? (d) If the length of the string is 10.0 cm, locate the nodes and teh antinodes. How many loops are formed in the vibration ?
View SolutionA sonometer wire resonates with a given tuning fork forming a standing wave with five antinodes between the two bridges when a mass of `9 kg` is suspended from the wire. When this mass is replaced by a mass 'M' kg, the wire resonates with the same tuning fork forming three antinodes for the same positions of the bridges. Find the value of `M`.
View SolutionThe equation of a stationary wave is given by `y=6sin.(2pix)/(3)cos40pit`. Where y and x are in cm and time t is in s. In respect to the component progressive waves, calculate
(a) amplitude (b) wavelength (c ) frequency
View SolutionAn open organ pipe has a length of 5 cm. (a) Find the fundamental frequency of vibration of this pipe. (b) What is the highest harmonic of such a tube that is in the audible range ? Speed of sound in air is `340 ms^-1` and the audible range is 20-20,000 Hz.
View SolutionAn open pipe is suddenly closed at one end with the result that the frequency of third harmonic of the closed pipe is found to be higher by `100 Hz` then the fundamental frequency of the open pipe. The fundamental frequency of the open pipe is
View SolutionA closed organ pipe of length `L` and an open organ pipe contain gass of densities `rho_(1)` and `rho_(2)`, respectively. The compressibility of gass are equal in both the pipes. Both the pipes are vibrating in their first overtone with same frequency . The length of the open orange pipe is
(a) `(L)/(3)`
`(4l) / (3)`
(c ) `(4l)/(3)sqrt((rho_(1))/(rho_(2)))`
(d) `(4l)/(3)sqrt((rho_(2))/(rho_(1)))`
View SolutionA source of sound of frequency 512 Hz is moving towards a huge reflector-wll, with a velocity of 10 m/s. Velocity of sound in air = 330 m/s. How many beats per second will be heard by an observer standing between the source and the wall?
View SolutionThree sound waves of equal amplitudes have frequencies `(v - 1), v, (v + 1)`. They superpose to give beats. The number of beats produced per second will be :
View SolutionA tuning fork arrangement (pair) produces 4beats/with one fork of frequency 288 c.p.s. A little wax is placed on the unknown fork and it then produces 2 beats/s. The frequency of the unknown fork is
View SolutionA vibrating tuning fork tied to the end of a string 1.988 m long is whirled round a circle. If it makes two revolutions in a second, calculate the ratio of the frequencies of the highest and the lowest notes heard by an observer situated in the plane of the tuning fork. Valocity of sound is 350 m/s.
View SolutionHow many times more intense is 20 dB sound compared to 10 dB sound?
View SolutionA car sounding a horn of frequency 1000 Hz passes an observer. The ratio of frequencies of the horn noted by the observer before and after passing of the car is 11 : 9. If the speed of sound is v , the speed of the car is
View SolutionA sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
View Solution
ILLUSTRATION questions and complete solutions for chapter OSCILLATIONS AND WAVES of MTG GUIDE PHYSICS (HINGLISH) of Class 11